4. Закон преломления

Рассмотрим примеры использования закона преломления света.

ПРИМЕР 1. ПОЛНОЕ ВНУТРЕННЕЕ ОТРАЖЕНИЕ

Из закона преломления следует, что при проникновении света из менее оптически плотной среды в более оптически плотную, угол  уменьшается: ₂ < ₁ (смотри рис. 2.6 А). В обратном случае, при переходе света из более оптически плотной среды в менее плотную, угол  возрастет (рис. 2.6 Б). Рассмотрим этот случай более подробно.

В эксперименте будем постепенно увеличивать угол падения ₁. В соответствии с законом преломления света (2.4), угол ₂ так же будет расти и в какой-то момент он достигнет 90⁰ - преломленный луч «заскользит» по границе раздела двух сред (рис. 2.6 В).

Р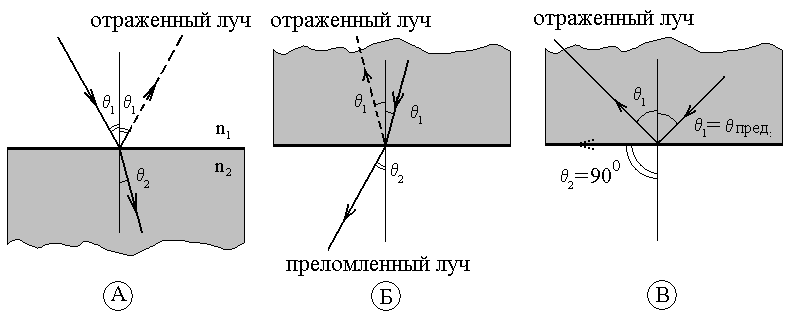 ис. 2.6 Различные случаи преломления света: А - проникновение света в оптически более плотную среду, Б - выход света в оптически менее плотную среду, В - полное внутреннее отражение. Свет, частично отраженный от границы раздела сред в случаях «А» и «Б», показан пунктиром. В случае «В» свет полностью отражается от границы, поэтому он показан сплошной линией.

У гол падения света, при котором преломленный луч направлен вдоль границы двух смежных сред, называется «предельный угол полного внутреннего отражения (_пред)».

Для предельного угла имеем:

n₁·sin _пред = n₂·sin 90⁰  n₂ (2.8)

Следовательно:

sin _пред = n₂ / n₁ (2.9)

или

_пред = arcsin (n₂/n₁) (2.10)

Ясно, что при углах падения   _пред , то есть от _пред до 90^0. световая волна вообще не проникает во вторую среду. Это явление называется «полное внутреннее отражение (ПВО)», так как из-за отсутствия преломленной волны вся энергия света будет заключена в отраженном световом луче.

НЕКОТОРЫЕ ЦИФРЫ:

Граница «Стекло-Воздух» : n_стекло =1.50. n_воздух =1  _пред = 41⁰48^/  42⁰

Граница «Алмаз – Воздух» : n_алмаз =2.42, n_воздух =1  _пред  24⁰

Явление ПВО широко используется в науке и технике. Например, поворотная призма в перископе или бинокле поворачивает луч света на 90⁰ практически без ослабления. В волоконных линиях связи (которые обеспечивают так называемый «Internet по оптическому каналу»), внутреннее отражение «запирает свет» внутри оптического волокна, позволяя передавать закодированную светом информацию на огромные расстояния.

Р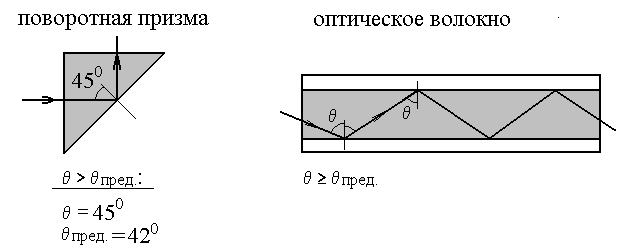 ис. 2.7 Полное внутреннее отражение света в поворотной призме и оптическом волокне

ПРИМЕР 2. ХОД ЛУЧА ЧЕРЕЗ ПЛОСКОПАРАЛЛЕЛЬНУЮ ПЛАСТИНУ

Прозрачное тело, ограниченное двумя параллельными плоскостями называется в оптике «плоскопараллельная пластинка». Примером такой пластинки может служить оконное стекло хорошего качества. Рассмотрим ход лучей в плоскопараллельной пластине:

Войдя в пластинку (точка А), луч света переходит из среды оптической менее плотной (воздух) в оптическую более плотную (стекло), поэтому он «приближается» к перпендикуляру (₂ < ₁). При выходе из пластинки (точка В) имеет место обратный процесс: ₃ > ₂.

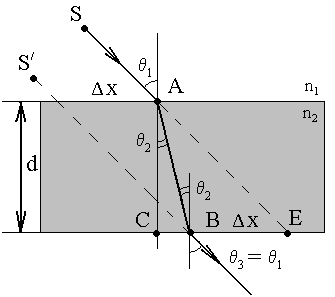
S - реальный источник света

S^/ - кажущийся («мнимый») источник света

Некоторые полезные соотношения:

CB=dtg ₂

CE=dtg ₁

х =ЕB=(CE-CB)=d(tg ₂ - tg ₁) - смещение луча

Рис. 2.8 Ход луча света через плоскопараллельную пластинку

Легко убедиться, что при прохождении пластинки луч не изменил своего направления, а только сместился. Для этого дважды запишем закон преломления:

Точка А: n₁·sin ₁ = n₂·sin ₂ (2.11)

Точка В: n₂·sin ₂ = n₁·sin ₃ (2.12)

Сопоставляя (2.11) и (2.12), мы заключаем, что ₃ = ₁.

Отчетливо заметное на рис. 2.8 боковое смещение луча (х) приводит к тому, что при рассматривании предметов сквозь плоскопараллельную пластинку, они будут казаться нам несколько смещенными относительно своего положения. В частности, вместо реального источника света S мы увидим «мнимый» источник S^/ . Величина х растет с увеличением толщины пластинки d, угла падения луча на пластинку ₁ или показателя преломления вещества пластинки n.

ПРИМЕР 3. ХОД ЛУЧА ЧЕРЕЗ ТРЕХГРАННУЮ ПРИЗМУ

Луч света, проходящий через призму, дважды изменяет свое направление (в точках А и В) и выходит преломленным в сторону ее основания:

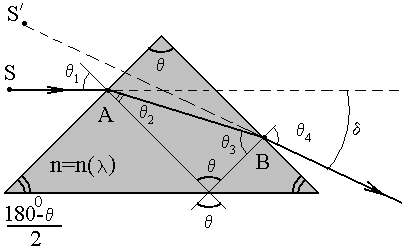
S - реальный источник света

S^/ - мнимый источник света

 -угловое отклонение луча

Рис. 2.9 Ход луча света через стеклянную призму

Наблюдателю кажется, что свет исходит не из точки S, а из точки S^/, расположенной на продолжении выходящего из призмы луча. Величина углового отклонения луча призмой  зависит от преломляющего угла призмы , угла падения луча на призму ₁ и показателя преломления призмы n. Здесь следует сделать важное замечание. Строго говоря, коэффициент преломления n не является постоянной величиной, а зависит от длины волны:   n=n(), причем n(«длинные волны») < n(«короткие волны»). Поэтому даже при равенстве всех прочих параметров, лучи света с разной длиной волны будут отклоняться призмой по-разному – волны с большей длиной всегда окажутся отклоненными на меньший угол , по сравнению с более короткими волнами.

Вывести формулу для  в общем случае сложно, этот вопрос мы рассматривать не будем. Интересующиеся могут познакомиться с численным примером подобных расчетов в книге: А.Г. Чертов, А.А. Воробьев. Задачник по физике. М.: «Наука», 2003г.

Для полноты картины, далее рассмотрим ещё один оптический элемент, использующий явление преломления света – линзу. Линзы важны для практики и обладают рядом особых свойств.