2. Четыре закона геометрической оптики

Основу геометрической оптики составляют четыре закона:

• Закон независимости световых лучей

• Закон прямолинейного распространения света

• Закон отражения света

• Закон преломления света

Д алее рассмотрим эти законы по отдельности:

Закон независимости световых лучей

При пересечении лучи не возмущают друг друга

Д ругими словами, каждый из лучей распространяется в пространстве так, как будто кроме него других лучей нет. Современные исследования показали, что внутри веществ данный закон справедлив только для не очень высоких интенсивностей света (характерных для привычных источников света). Для лучей мощных лазеров он нарушается.

Закон прямолинейного распространения света

В однородной среде свет распространяется прямолинейно

О тметим, что имеется ряд случаев, в которых данный закон оказывается приближенным. В частности, при прохождении света через небольшие отверстия наблюдается проникновение света в область геометрической тени. Отклонение от прямолинейного характера распространения тем больше, чем меньше размеры отверстия (вспомните явление дифракции света).

Закон отражения света

О траженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной точке падения; при этом угол отражения равен углу падения

Р ис. 2.1 Пояснения к закону отражения света

Закон преломления света

П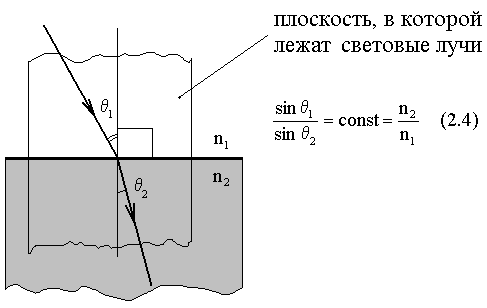 реломленный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; при этом отношение синуса угла падения к синусу угла преломления есть величина, постоянная для двух данных веществ

Рис. 2.2 Пояснения к закону преломления света

Сделаем некоторые замечания:

1. Иногда входящую в формулу (2.4) const = n₂/n₁ обозначают «n₂₁» и называют «относительный показатель преломления 2-го вещества по отношению к 1-му».

2. Вещество с большим показателем преломления принято называть «оптически более плотная среда», а вещество с меньшим показателем - «оптически менее плотная среда».

3. Часто закон преломления формулируют в другой, более удобной для запоминания форме:

n₁·sin ₁=n₂·sin ₂ (2.5)

По историческим причинам, выражение (2.5) называется «закон Снелиуса» (1620г). В современном виде этот закон был записан Декартом (1637г).

3. Принцип Ферма

Перед тем, как рассмотреть следствия из закона преломления света, а так же примеры его использования, уместно сделать ещё одно отступление. Ещё в середине XVII века, то есть во времена Снелиуса и Декарта, французский математик Ферма¹ сформулировал простой принцип, из которого сразу вытекают три основных закона геометрической оптики: законы прямолинейного распространения света, отражения и преломления. В последствии этот принцип был назван в его честь.

П ринцип Ферма

Свет распространяется по такому пути, для прохождения которого ему требуется минимальное время

Запишем данным принцип в виде формулы:

(2.6)

Так как скорость света в вакууме c есть величина постоянная, то для достижения минимума выражения (2.6) достаточно минимизировать величину «Ln», которую называют «оптическая длина пути»:

L· n→ minimum (2.7)

Кроме того, если свет не пересекает границы раздела нескольких веществ (то есть распространяется только в пределах некоторого одного вещества), при отыскании минимума выражения (2.7) величину n можно не учитывать.

Покажем, как из принципа Ферма (2.7) вытекают законы геометрической оптики.

• Произвольным образом отметим две точки: точку А и точку Б (смотри рис. 2.3). Пусть нас интересует путь света А→Б, для его нахождения воспользуемся принципом Ферма.

И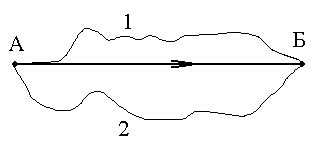 звестно, что кратчайший путь между двумя заданными точками – это прямая, поэтому траектории 1 и 2 не будут реализованы. Итак, естественным образом мы пришли к закону закон прямолинейного распространения света.

Рис. 2.3 Принцип Ферма: установление характера распространения света

• М 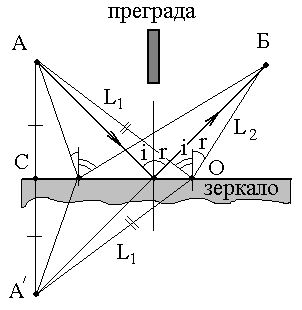ежду точками А и Б поместим непрозрачную преграду, а снизу – зеркало. Учитываем закон прямолинейного распространения света.

Рис. 2.4 Принцип Ферма: установление закона отражения света

В данном случае путь света складывается из двух отрезков: АО = L₁ и ОБ = L₂. Требуется найти такое положение точки О, чтобы L=L₁+L₂ было минимально.

Для отыскания искомого положения, воспользуемся точкой А^/, симметричной точке А относительно поверхности зеркала («отражением точки А в зеркале»). По принципу построения А^/СО и АСО равны, а значит отрезок АО = отрезку А^/О (отмечены двойными засечками на рисунке). Легко заметить, что величина L – это длина ломаной А^/ОБ. Поэтому минимум длины L соответствует ситуации, когда ломаная линия превращается в прямую линию. В этом случае (из соображений симметрии) угол отражения r, будет равен углу падения i. Тем самым, мы только что установили закон отражения света!

• З акон преломления можно получить, используя аналогичные рассуждения. Выберем точки А и Б внутри двух разных веществ с коэффициентами преломления n₁ и n₂. Для определенности, пусть n₂ > n₁.

Рис. 2.5 Принцип Ферма: установление закона преломления света

Из рисунка видно, что путь света складывается из двух частей - отрезка АО = L₁ и ОБ = L₂. Так как свет пересекает границу раздела двух сред, то в выражение (2.7) длины отрезков входят с учетом коэффициентов преломления веществ: Ln  L₁n₁+L₂n₂. Требуется отыскать такое положение точки О, чтобы оптическая длина пути «Ln» было минимальна.

В данном случае, только путем выполнения некоторых геометрических построений найти оптимальное положение точки уже нельзя, необходимы дополнительные тригонометрические расчеты. Можно показать, что для достижения минимума оптической длины пути необходимо и достаточно, чтобы отношение синуса угла падения «sin₁» к синусу угла преломления «sin₂» в точности подчинялись формуле (2.4) - закону преломления.