4. Цветовой график системы xyz

Ц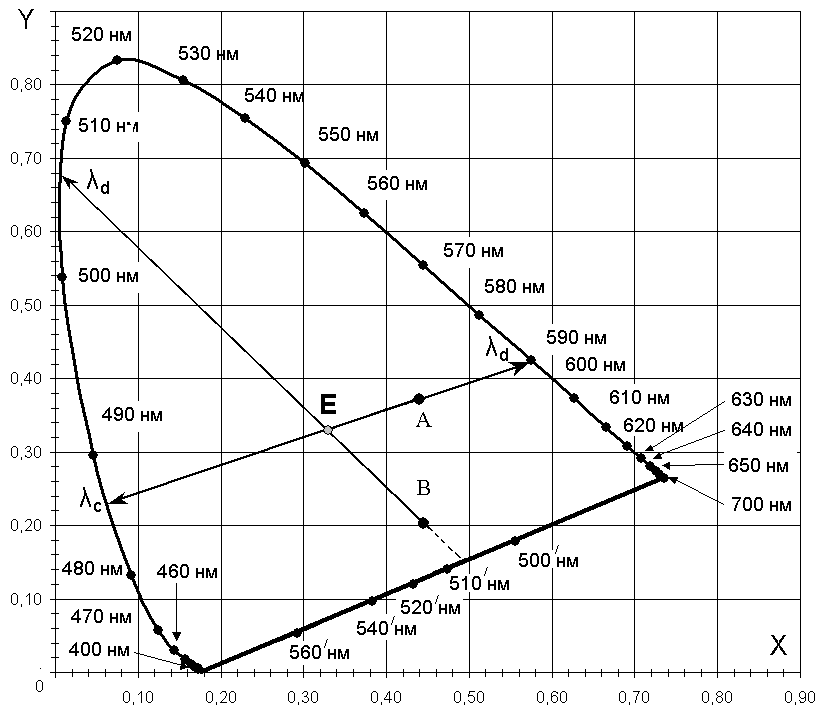 ветовой график системы XYZ имеет вид:

Рис. 9.7 Цветовой график системы XYZ

Точка Е - равноинтенсивный (равностимульный ) белый цвет. Точки А и В - некоторые цвета.

• Преобладающая длина волны (λ_d) на цветовом графике системы XYZ

Чтобы определить преобладающую длину волны λ_d для некоторого заданного цвета А, необходимо из точки Е через точку цвета провести луч до пересечения с границей поля реальных цветов. Для нахождения длины волны дополнительного цвета λ_с, луч проводят в противоположную сторону, так же до пересечения с границей поля реальных цветов.

Отметим важные особенности пурпурных цветов:

(1) Если точка λ_с принадлежит линии пурпурных цветов, то для такого цвета дополнительного не существует

(2) Пурпурные цвета являются сложными (представляют собой смесью красных и фиолетовых цветов), поэтому их характеризуют особым образом. Для нахождения λ_d луч направляют не к линии пурпурных цветов, а в противоположную сторону, в сторону спектрального локуса. При этом, рядом с найденным числом ставится знак « ^/ » или «–». Например, для точки В: «λ_d = – 506 нм» или «λ_d ^/ = 506 нм».

• Колориметрическая чистота (P_К) на цветовом графике системы XYZ

Колориметрическая чистота некоторого цвета А (см. рисунок 9.7) определяется его удаленностью от точке белого цвета Е: чем точка А ближе к точке Е, тем чистота меньше, и наоборот, чем точка А ближе к спектральному локусу, тем чистота больше. По известным координатами цветности {x,y}, колориметрическая чистота вычисляется следующим образом:

или

- через координаты «х» (9.21)

- через координаты «y», (9.22)

где x_ и y_ - координаты спектрально - чистого цвета «λ_d» того же тона, что и данный цвет (точка «преобладающей длины волны» для данного цвета»), для пурпурных цветов x_λ и y_λ берутся на линии пурпурных цветов;

x_Е и y_Е - координаты точки Е (так называемого «опорного белого цвета»), обычно полагают x_Е≈y_Е≈1/3.

И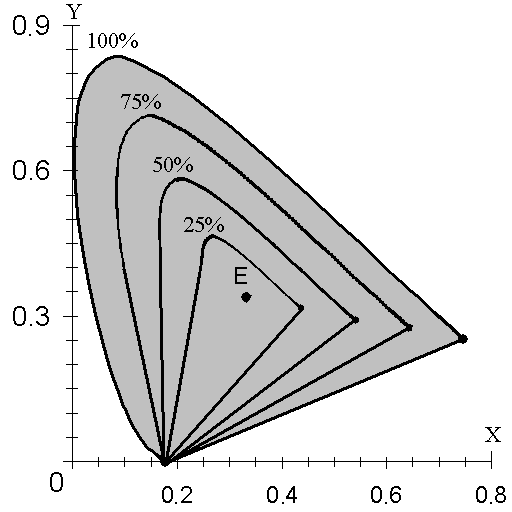 так, формула (9.21) или (9.22) позволяет выразить колориметрическую чистоту через координаты цветности. Для удобства вычислений, на цветовом графике обычно нанесены так называемые «линии равной условной чистоты» (другое название: «линии равной условной насыщенности »).

Условная насыщенность Р_В вводится по формулам:

или

- через координаты «х» (9.23)

- через координаты «y» (9.24)

Рис. 9.8 Цветовой график системы XYZ с нанесенными линиями условной насыщенности

Сравнивая формулы для колориметрической чистоты (9.21) и (9.22) с формулами (9.23) и (9.24) для условной чистоты, получаем:

(9.25)

Рассмотрим два крайних случая использования формулы (9.25):

1. Для цветов, расположенных вблизи точки Е : Р_в ≈ 0  Р_K ≈ 0.

2. Для цветов вблизи локуса: Р_в ≈ 100%, y_/y ~1  Р_K ≈ 100%

Нетрудно заметить, что в приведенных примерах Р_K ≈ Р_в. Таким образом, для цветов с малой и с большой условной чистотой Р_в колориметрическую чистоту цвета Р_K можно приближено прировнять условной чистоте цвета.

• Аддитивное сложение двух цветов на цветовом графике системы XYZ

Цвет аддитивной смеси двух излучений Ц  лежит на отрезке, соединяющем точки смешиваемых цветов. Точка Ц разделяет отрезок Ц₁Ц₂ на две части, длины которых обратно пропорциональны модулям смешиваемых цветов:

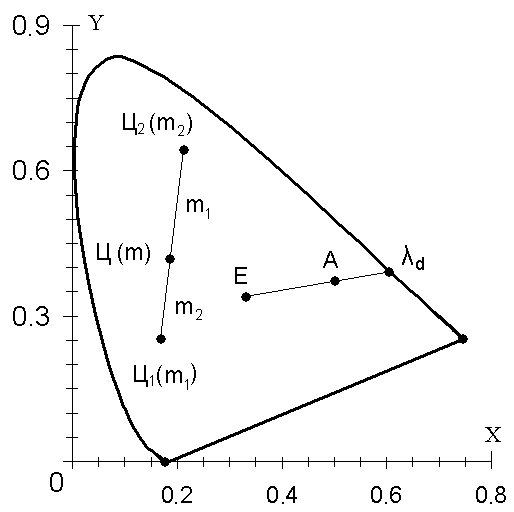« Первый цвет» Ц₁ → цветовой модуль «m_1»

«Второй цвет» Ц₂ → цветовой модуль «m₂»

Ц = Ц₁+Ц₂– суммарный цвет:

m = m₁+m₂,

Таким образом, чтобы изготовить цвет, обозначенный на цветовом графике точкой А, необходимо смешать спектрально-чистый цвет того же тона «_d» и белый цвет «Е» в соотношении:

Рис. 9.9. Нахождение результата аддитивного смешивания двух цветов (в системе XYZ)

Отметим, что результат сложения нескольких цветов может быть найден и чисто аналитически, без использования цветового графика. Действительно, согласно свойствам цветовых векторов:

(9.26)

где X₁, Y₁, Z₁- цветовые координаты первого из складываемых цветов (Ц₁), X₂, Y₂ , Z₂- цветовые координаты второго из складываемых цветов (Ц₂), X, Y , Z - цветовые координаты суммарного цвета (Ц= Ц₁+Ц₂).

В нашем случае цвета заданы по-другому, своими координатами цветности: Ц₁{x₁, y₁}, Ц₂{x₂, y₂}. Поэтому перед тем как воспользоваться формулами (9.26), необходимо вычислить цветовые координаты {X_i, Y_i, Z_i } для каждого из складываемых цветов, основываясь на знаниях об их «количестве».

Для простоты, предположим, что количества складываемых цветов заданы посредствам указания из цветовых модулей: Ц₁ m₁, Ц₂m₂. Используя последовательно формулы (9.15) и (9.26) получаем:

, (9.27)

где {x, y} - искомые координаты цветности суммарного цвета Ц.