2. Графическое представление цветов в системе rgb

К ак мы уже знаем, любой цвет однозначно характеризуется тремя цветовыми координатами–количествами основных цветов системы RGB: Ц{R,G,B}. Другими словами, цвет является вектором в некотором трехмерном пространстве. Естественно считать, что все цветовые векторы имеют общее начало, которое соответствует «нулевому количеству цвета» – чёрному цвету.

Н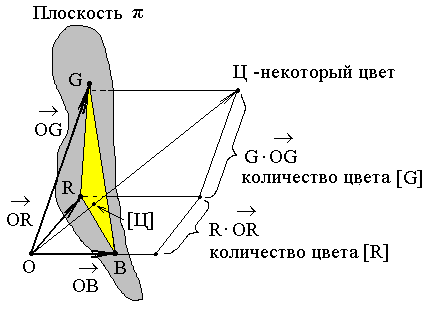 аправим векторы основных цветов произвольным образом, но так, чтобы они не лежали в одной плоскости:

Цветовые векторы складываются по обычным правилам, следовательно:

• Если цвет Ц описывается положительными количествами основных цветов, то его цветовой вектор будет лежать внутри треугольной пирамиды, построенных на векторах . Если одна из координат вектора будет отрицательна, то вектор расположится вне пирамиды.

Рис. 9.3 Цветовое пространство

• Так как при аддитивном сложении цветов никогда не образуется чёрный цвет, то не существует цветовых векторов с диаметрально противоположными направлениями. Поэтому всевозможные цветовые вектора заполняют не всё пространство, а лишь некоторую его часть.

• Рассмотрим треугольник ΔRGB, полученный при соединении концов векторов основных цветов - так называемы «треугольник единичных цветов». Концы векторов, соответствующих всевозможным единичными цветами [Ц] (цветам, для которых модуль цвета m равен единице) будут лежать в плоскости π, содержащей данный треугольник. Действительно, уравнение для координат точки, принадлежащей плоскости π и уравнение для координат вектора единичного цвета совпадают: r+q+b =1

Координаты {R,G,B} векторов Ц, соответствующих различным спектрально-чистым цветам были экспериментально определены Райтом и Гилдом. По известным координатам можно построить эти вектора, и тем самым нанести на плоскость π точки всех существующим в природе чистых цветов – получить так называемый «цветовой график»:

Ц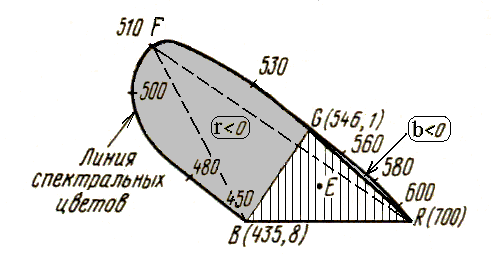 ветность произвольной смеси монохроматических излучений всегда изображается точкой {r, g, b}, лежащей внутри фигуры, ограниченной замкнутой линией BFGRB. Поэтому данная фигура называется «поле реальных цветов».

Рис. 9.4 Цветовой график системы RGB

Точкой Е на рисунке обозначен равноинтенсивный белый цвет

Введем еще несколько определений:

Л иния, на которой расположены точки цветности всех монохроматических излучений называется линия спектральных цветов или спектральный локус.

Л иния, соединяющая точки цветности основного красного и основного синего цветов (т. R и т. B) называется линия пурпурных цветов, на ней расположены максимально насыщенные пурпурные цвета.

Отметим две важные особенности цветового графика:

1. Цветов с отрицательным значением координаты b (закрашенная область « b < 0 » на рисунке 9.4) очень мало, поэтому в большинстве практических расчетов можно считать, что для этих цветов b=0.

2. Цветов с отрицательным значением координаты r (закрашенная область « r < 0 » на рисунке 9.4) очень много: они располагаются вне ΔRGB, на площади ограниченной отрезком BG и кривой BFG.

Указанный недостаток снижает точность вычислений и не может быть устранен выбором вместо RGB другой триады основных цветов, так как не один треугольник с вершинами в точках, соответствующих реальным цветам, не охватывает спектральный локус (смотри, например, ΔRFB).