2. Законы Грассмана

Б олее обобщённую и строгую форму законам аддитивного («оптического») сложения цветов в 1853г. придал немецкий математик Х. Грассман. Он сформулировал три закона, которые впоследствии назвали в его честь. В различных источниках авторы формулируют их по-разному, предлагаемая ниже форма является одним из вариантов.

1 Закон

Любой цвет может быть выражен через три линейно – независимых цвета, при этом количество всевозможных триад цветов бесконечно велико.

Сделаем некоторые пояснения. По определению, несколько цветов называются линейно – независимыми, если каждый из них не может быть получен смешением оставшихся. «Триада» – это набор (или тройка) из трех цветов, их можно составить бесконечно много. Вот два примера троек линейно-независимых цветов: {К,З,С} и {Ж,Г,П}.

Для триады {К,З,С} I закон Грассмана выглядит так:

, (8.3)

где К, З и С – характеризуют количество соответственно цветов [К], [З] и [С], необходимое для получения цвета Ц. Отметим, что знак “=“ подразумевает не точное равенство спектров излучения, а так называемую «визуальную тождественность» - для человеческого глаза цвет Ц и цвет, полученный смешиванием выбранных трех цветов неотличимы (то есть при установлении визуального тождества используется свойство метамеризма цвета).

У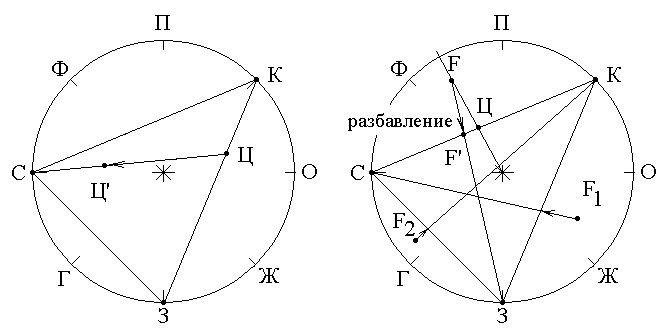 бедимся, что любой цвет изображенный точкой на цветовом круге действительно может быть представлен в виде суммы трех основных цветов, например [К], [З] и [С]:

Рис. 8.3 Пояснения к первому закону Грассмана

1. Из рисунка 8.3 видно, что при смешивание [К] и [З] в различных пропорциях мы получаем цвета Ц лежащие внутри отрезка КЗ.

2. При добавлении к [К] и [З] третьего цвета [С], результирующий цвет (Ц^/) смещается «в сторону [С]» - переходит на отрезок ЦС. Ясно, что смешивая цвета [К], [З] и [С] в различных соотношениях, мы получим все цвета, заключенные внутри треугольника КЗС.

При каких же условиях может быть получен цвет, лежащий вне треугольника, например F? Ясно, что смесь цветов [С] и [К] способна дать тот же световой тон, но только меньшей насыщенности (т. Ц). Следовательно, для достижения цветового тождества, F необходимо предварительно «разбавить» - добавив к искомому цвету F немного другого цвета, например [З], мы получим F^/, который уже лежит внутри КЗС. Цвет F^/ уже может быть «изготовлен» путем смешивания основных цветов [С] и [К]. Итак, при разбавлении мы имеем:

(8.4)

Сравнив последнюю строчку (8.4) и (8.3) мы видим, что так же как и в предыдущем случае, для получения цвета F нужно смешать три основных цвета, в количестве {К, С, -З}. Единственное отличие заключается в том, что цвет «[З]» теперь нужно взять в «отрицательном количестве». Таким образом, хотя физически (то есть в эксперименте по смешиванию цветов [К], [З] и [С]) цвет F получить невозможно (так как нельзя взять цвет в отрицательном количестве), тем не менее, он может быть формально описан определенными количествами трех основных цветов.

Совершенно аналогично, используя «отрицательные количества» цветов, могут быть описаны и все остальные цвета вне КЗС, например F₁ - отрицательное количество цвета [С] или F₂ - отрицательное количество цвета [К].

И так, мы убедились, что используя I закон Грассмана любому цвету действительно могут быть однозначно поставлены в соответствие три величины, своеобразные «три цветовые координаты», то есть цвет оказывается подобен вектору в некотором 3х мерном пространстве – так называемом «цветовом пространстве».