3. Элементы фотометрии

Подробно рассмотрев качественные характеристики излучений (спектры) различных источников, перейдем к методам описания количества света. Такие методы изучаются в особом разделе оптики - «фотометрия». Фотометрия измеряет количество света с точки зрения яркостных ощущений некоторого наблюдателя:

П

Свет

риборы, измеряющие энергию излучения  Энергетические характеристики

Наблюдатель, его яркостные ощущения  Фотометрические характеристики

Так как ощущения несут отпечаток индивидуальных особенностей конкретного человека, то данный подход может содержать в себе элемент субъективности. Чтобы полностью исключить двусмысленность в результатах измерений, МКО провела специальные исследования: на экран проецировались световые потоки, отличающиеся по длине волны и по мощность, испытуемых просили охарактеризовать яркость света.

Оказалось, что глаз наблюдателя обладает неодинаковой чувствительностью к различным волнам. В зависимости от длины волны  , одно и тот же количество света вызывает разные зрительные ощущения. Чувствительность глаза достигает максимума при =556 нм и плавно спадает к краям видимого диапазона.

У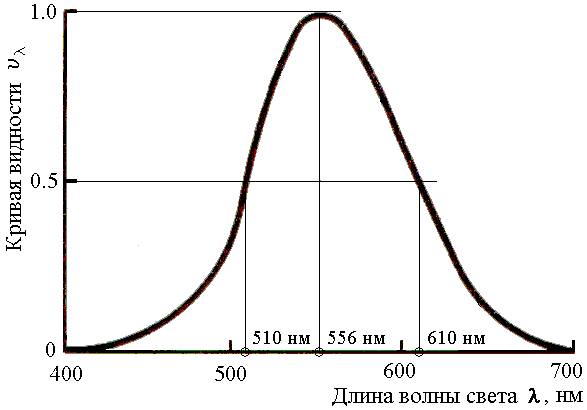 средненная закономерность восприятия света с различной длиной волны человеком – так называемое «восприятие света стандартным наблюдателем МКО» – была в 1924г оформлена в виде международного стандарта.

Рис. 5.4 Стандартная функция относительной видности

Из рисунка 5.4 видно, что энергетические характеристики света (измеряемые каким-либо «беспристрастным» прибором) и фотометрические характеристики света, связанные с ощущениями наблюдателя сильно отличаются!

Последовательно познакомимся с основными фотометрическими характеристиками.

1. Световой поток (Ф)

   • Для простоты, сначала предположим, что источник излучает монохроматическое излучение с известной длины волны  и мощностью Р.

Мощность излучения – это энергия, испущенная источником в единицу времени, измеряется в «Ваттах» (Вт):

P =E/t (5.3)

Для перехода к световым ощущения наблюдателя, учитываем стандартную видность _ и стандартный переводной коэффициент «683 лм/Вт»:

Ф =E/t_683 (5.4)

Используя (5.3) и (5.4), получаем окончательное выражение для светового потока:

Ф = 683  Р_ (5.5)

• Если источник испускает свет со сложным спектром, то расчеты усложняются.

Для описания спектра вводится Р_ – «спектральная плотность лучистой энергии» или просто «спектральная плотность энергии». По определению:

, (5.6)

где Е(; +) – энергия, приходящаяся на волны, длины которых попадают в интервал (: +); Р(: +)-мощность, соответствующая этой энергии.

Спектральная плотность энергии измеряется в «Ваттах, приходящихся на 1нм» (Вт/нм) и является аналогом мощности Р для монохроматического излучения.

Из определения (5.6) следует, что на интервал длин волн  приходится мощность Р:

(5.7)

Используя последовательно (5.5) и (5.7), получаем соответствующий этой мощности световой поток:

(5.8)

Полную мощность и полный световой поток некоторого источника света получают суммированием соответственно выражений (5.7) и (5.8) по всевозможным длинам волн:

(5.9)

(5.10)

где «380 нм» и «780 нм» - границы видимой области спектра.

ЗАМЕЧАНИЕ

Чтобы определить цвет несамосветящегося предмета необходимо знать, как тело отражает / пропускает внешнее световое излучение. Для этого указывают коэффициенты отражения / пропускания тела. Данные величины вводятся следующим образом (по определению) :

- коэффициент отражения (5.11)

- коэффициент пропускания (5.12)

2. Сила света (I)

С ила света численно равна отношению светового потока Ф к телесному углу , в пределах которого этот поток распространяется:

(5.13)

Сила света измеряется в «канделах» (кд). В отличие от светового потока, эта величина является одной из основных в системе СИ - в городе Севр (Франция) в палате мер и весов хранится ее эталон.

Чтобы пояснить ранее не встречавшееся геометрическое понятие «телесный угол», введем в рассмотрение так называемый «точечный источник»:

Е 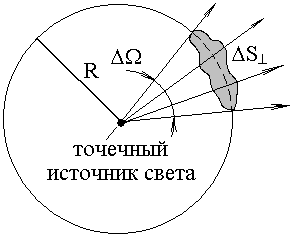сли размеры источника малы по сравнению с расстоянием от него до точки наблюдения, то такой источник называется точечным.

Рис. 5.5 Пояснения к определению телесного угла

В задачах источники света обычно полагают точечными. Окружим точечный источник воображаемой сферической оболочкой радиуса R (см. рис.5.5). На поверхности сферы мы увидим освещенное пятно площадью S_. Ясно, что размеры пятна характеризуют степень направленности излучения⁵. Однако, даже для одного и того же источника, площадь пятна будет зависеть от выбора радиуса оболочки. Отношение «S_/R²» так же характеризует направленность, но от радиуса уже не зависит. Данную величину назвали «телесный угол» (), она является обобщением обычного плоского угла на случай трехмерного пространства. Телесный угол принято измерять в «стерадианах» (ср). По определению:

 = S_/R² (5.14)

Нетрудно заключить, что максимально возможный телесный угол составляет 4R²/R²= 4 ср.

Введем еще одно понятие:

Е сли источник излучает свет равномерно по всем направлениям, то он называется изотропным.

Для изотропного источника сила света I и полный световой поток Ф связаны простейшим соотношением:

Ф = 4I (5.15)

3. Освещенность (Е)

О свещенность численно равна отношению светового потока Ф, к площади поверхности S на которую он падает:

(5.16)

Освещенность измеряется в «люксах» (лк).

Рис. 5.6 Пояснения к выводу формулы для освещенности

Знание освещенности важно для практики – в частности, рабочие места должны быть оптимально освещены. Недостаток света снижает производительность труда и может даже повредить здоровью (например, зрению) сотрудников. Избыток света приведет к неоправданному перерасходу электрической энергии.

НЕКОТОРЫЕ ЦИФРЫ:

Освещенность поверхности Земли в полдень – 10⁵ лк

Оптимальная освещенность рабочего стола для сборки часов и шитья – 300 лк

Оптимальная освещенность рабочего стола для чтения – 3050 лк

Совместное использование определений для силы света, освещенности и телесного угла – соответственно (5.13), (5.16) и (5.14) – позволяет вывести простую формулу, удобную для практических расчетов освещенности. Действительно:

Используем определение телесного угла: (5.17)

Используем определение силы света: (5.18)

Используем определение для освещенности: (5.19)

Теперь рассмотрим величины, характеризующие источники света.

4. Светимость (М)

С ветимость численно равна отношению светового потока Ф_исп , к площади светящейся поверхности S, с которой он был испущен:

(5.20)

Чтобы не путать с освещенностью, светимость измеряют в «люменах, приходящихся на 1м²» (лм/м²).

Светимость обычно используют для описания протяженных источников, различные участки которых могут по-разному испускать свет. Отметим, что свечение тел может возникать не только вследствие протекания некоторых внутренних процессов, но и за счет отражения поверхностью падающего света или за счет рассеяния (пример: свет Луны). В этом случае под Ф^исп подразумевают соответственно отраженный или рассеянный данным элементом поверхности световой поток (во всевозможных направлениях!).

5. Яркость (В)

Я ркость численно равна отношению силы света I, испущенного некоторой поверхностью, к площади этой поверхности S_ ⁶ :

, (5.21)

Яркость измеряют в «канделлах, приходящихся на 1м²» (кд/м²). Эта фотометрическая величина характеризует излучение, испущенное в заданном направлении.

НЕКОТОРЫЕ ЦИФРЫ:

Яркость поверхности Солнца – 1510⁸ кд/м²

Яркость спирали лампы накаливания  210⁸ кд/м²

Яркость экрана ТВ – 2550 кд/м²

Яркость среднестатистического ночного неба – 10 кд/м²

Для удобства использования, иногда определение яркости переписывают в другом виде – подставив в (5.21) явные выражение для силы света I и площади S_:

, (5.22)

где  - угол между перпендикуляром к светящейся поверхности и световыми лучами.

Введем в рассмотрение так называемый «ламбертовский источник света»:

И сточник называется ламбертовским, если его яркость одинакова во всех направлениях:

B = const

Оказалось, что для данного источника света, выражение (5.22) может быть преобразовано к максимально простому виду. Действительно, используя определение яркости в форме (5.22) легко выразить световой поток , испущенный элементом источника с площадью S в направлении :

=BScos  (5.23)

Выполнив суммирование по всевозможным направлениям (в пределах полного телесного угла 4) , можно получить полный световой поток, испущенный элементом S:

(5.24)

Для ламбертовского источника B=const и интеграл легко вычисляется:

(5.25)

С другой стороны, из определения светимости (5.20) следует, что испущенный источником во всевозможных направлениях световой поток Ф_исп равен:

(5.26)

Приравниваем формулы (5.25) и (5.26), сокращаем S, выражаем яркость B. Искомое соотношение получено:

(5.27)