2.4. Трудомісткість рекурсивних реалізацій алгоритмів

Більшість сучасних мов високого рівня підтримують механізм рекурсивного виклику, коли функція, як елемент структури мови процедурного програмування, може викликати сама себе з іншим аргументом. Ця можливість дозволяє напряму реалізувати обчислення рекурсивно обчислювальних функцій. Відзначимо, що в силу тезису Черча - Тьюринга апарат рекурсивних функій Черча рівносильний машині Тьюринга, отже, любий ітераційний алгоритм може бути реалізований рекурсивно.

Роздивимось приклад рекурсивної функції, що обчислює значення факторіала цілочисельного аргументу:

long Factorial(int n){

long F;

if((n==0)||(n==1)) // перевірка можливостей прямого обчислення

F=1;

else F=n*Factorial(n-1); // рекурсивний виклик функції

return F;

}

Аналіз трудомісткості рекурсивних реалізацій алгоритмів, очевидно, залежить як від кількості операцій, виконаних при одному виклику функції, так і від кількості таких викликів. Графічне уявлення породжуваного даним алгоритмом ланцюга рекурсивних викликів називається деревом рекурсивних викликів. Більш детальний розгляд призводить до необхідності урахування затрат на організацію виклику функції і передачу параметрів. Повинні бути також враховані і затрати на повернення обчислених значень і передачу управління на точку виклику. Ці операції повинні бути включені в функцію трудомісткості рекурсивно заданого алгоритма.

Можна також зауважити, що деяка гілка дерева рекурсивного виклику обривається при досягненні такого значення параметра, при якому функція може бути обчислена безпосередньо. Таким чином, рекурсія еквівалента конструкції циклу, в якому кожен прохід є виконанням рекурсивної функції з заданим параметром.

Розглянемо на прикладі Рис.2.2 організацію рекурсії для функції обчислення факторіалу.

Д ерево рекурсивних викликів може мати і більш складну структуру, якщо на кожному виклику породжується декілька звертань. Зауважимо, що при кожному рекурсивному виклику виконується ряд операцій, обслуговуючих цей виклик. Це призводить до необхідності аналізу трудомісткості обслуговування рекурсії.

Механізм виклику функції або процедури в мові високого рівня істотно залежить від архітектури комп’ютера і операційної системи. В рамках архітектури і операційних систем ІВМ РС сумісних комп’ютерів цей механізм реалізований за допомогою стека. Як фактичні параметри, що передаються в процедуру або функцію, так і значення, що повернулися з них, розміщуються в програмному стеку спеціальними командами процесора. Додатково зберігаються значення необхідних регістрів і адреса повернення в викликаючу процедуру. Схематично цей механізм проілюстрований на Рис. 2.3.

Д ля підрахунку трудомісткості виклику будемо рахувати операції додавання слова в стек і виштовхування зі стека елементарними операціями, відповідними з операцією присвоєння. Тоді при виклику процедури або функції в стек поміщається адреса повернення, стан необхідних регістрів процесора. Після цього виконується перехід по адресі на викликану процедуру, яка витягує передані фактичні параметри, виконує обчислення, поміщає результат за зазначеними в стеку адресами, і при завершенні роботи відновлює регістри, виштовхує зі стеку адресу повернення і здійснює перехід за цією адресою.

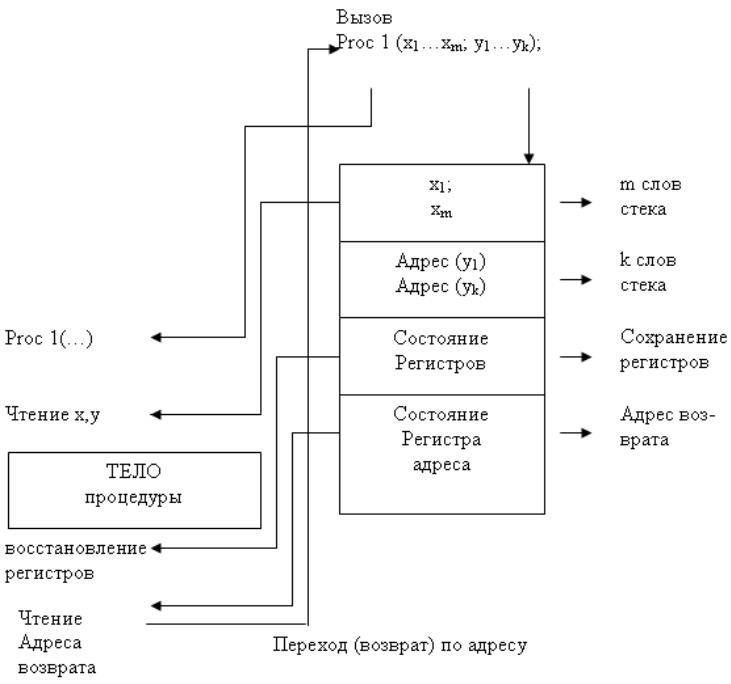
Рис. 2.3. Механізм виклику процедури з використанням програмного стеку

При завершенні роботи викликана процедура відновлює регістр, вилучає зі стеку адресу повернення і виконує перехід по цій адресі.

Для аналізу трудомісткості виклику/повернення введемо значення:

m -- кількість переданих фактичних параметрів,

k -- кількість повернених по адресному посиланню значень,

r -- кількість збережених в стеку регістрів.

Тоді трудомісткість в елементарних операціях на один виклик і повернення буде виглядати так:

(2.5)

Аналіз трудомісткості рекурсивних алгоритмів і в деякій частині трудомісткість самого рекурсивного виклику можливо виконати різними способами в залежності від того як формується кінцева сума елементарних операцій:

- окремо по ланцюгам рекурсивних викликів і повернень;

- загалом по вершинам дерева рекурсивних викликів.

Продемонструємо цей підхід на прикладі рекурсивного обчислення факторіала:

long Factorial(int n){

long F;

if((n==0)||(n==1)) // 3 елементарні операції

F=1; // 1 елементарна операція

else F=n*Factorial(n-1); // 3 елементарні операції

return F;

}

Кількість вершин рекурсивного дерева, дорівнює, очевидно, n, при цьому передається і повертається по одному значенню а на останньому рекурсивному виклику значення функції обраховується безпосередньо. Остаточно, у припущенні про збереження чотирьох регістрів отримаємо:

зауважимо що n - параметр алгоритму, а не кількість слів на вході.