Распределение коммерческих банков по интервалам по размеру кредитных вложений (или по объему вложений в ценные бумаги)

№ банка	Интервала	Интервал по разм. кредит. влож. (по объему влож. ценных бумаг)	Число банков по интервалу	Собственный капитал млн. руб.	Объем кредитных вложения млн. руб.	Объем вложений в ценные бумаги млн. руб.	Балансовая прибыль млн. руб.
1	2	3	4	5	6	7	8
	I		-
			-
		и т.д.					
		Итого:
	II		-
			-
			-
		и т. д.	-
		Итого:					
		Всего:					

Суммы ()^(Всего) сверяются с итоговыми результатами подсчитанными по графам из условия задания.

По итогам интервалов (групп) строим сводную групповую таблицу 2.

Таблица 2

Группировка коммерческих банков по размеру кредитных вложений (или по объему вложений в ценные бумаги)

№ п.п.	Интервал млн. руб.	Количество банков		Кредитные вложения (объем влож. в ценные бумаги) млн. руб.		Исследуемый (факторный) признак		Размер прибыли на 1 рубль кредитных вложений (1 руб. объема вложений в ценные бумаги)
		ед	В % к итогу	Всего	на 1 банк	Всего	На 1 банк
1	2	3	4	5	6	7	8	9
	Итого:

Основные статистические формулы, которые следует применить при решении данной задачи, следующие:

1. Формула Стерджесса для определения оптимального числа групп

где - число групп (целое число);

- число единиц выборочной совокупности.

lg 24 = 1,33

lg 25 = 1,38

lg 26 = 1,41

lg 27 = 1,43

lg =

2. Величина равного интервала

,

где , т.е. размах вариации;

- наибольшее значение признака в совокупности;

- наименьшее значение признака в совокупности.

По результатам группировки необходимо определить относительную величину структуры и построить круговую диаграмму.

По результатам группировки требуется построить полигон и гистограмму распределения.

При выполнении пункта 2.2. «Исчисление средних величин и показателей вариации на основании группировки» надо изучить способы вычисления средних величин и показателей вариации.

По полученным в результате группировки данным интервального вариационного ряда распределения нужно исчислить среднюю, дисперсию, среднее квадратическое отклонение и коэффициент вариации. При определении среднего значения признака по группам следует помнить, что величина открытого интервала первой группы приравнивается к величине интервала второй группы, а величина открытого интервала последней группы - к величине интервала предпоследней группы (если в результате группировки получен интервальный ряд с открытыми интервалами).

Основные формулы, которые используются в расчетах, следующие:

1. Средняя арифметическая взвешенная

,

где - -ая варианта признака;

- средняя величина признака;

f - частота признака.

2. Дисперсия вариационного признака для среднего показателя взвешенная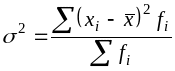

3. Среднее квадратическое отклонение взвешенное

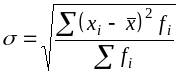
4. Коэффициент вариации

V= 100%

Результаты расчетов представить в виде табл. 3.

Таблица 3

Расчет средней величины, дисперсии и среднего квадратического отклонения

№ группы	Величина интервала, млн. руб.	Середина интервала	Количество единиц в интервале (частота),
1	2	3	4	5	6	7	8

При выполнении пункта 2.3. «Исчисление ошибки выборки и определение оптимального объема выборки» надо изучить выборочный метод в статистике, уяснить понятия генеральной и выборочной совокупностей, их характеристики.

Основные формулы, которые используются в расчетах, следующие:

1.Возможная граница генеральной средней:

,

где - предельная ошибка выборочной средней (для бесповторного отбора).

2.Возможная граница генеральной доли:

,

где выборочная доля w – это удельный вес единиц в выборке, обладающих альтернативным признаком: ,

где m - число единиц в выборке, обладающих альтернативным признаком;

n - число единиц выборочной совокупности.

3.Дисперсия альтернативного признака или доли вычисляется по формуле:

=w(1-w), тогда

- предельная ошибка выборочной доли (для бесповторного отбора).

4. Необходимый объем выборки при бесповторном случайном отборе определяется по формуле:

n= ,

где t=1 Ф(t)=0,683; t=2 Ф(t)=0,954; t=3 Ф(t)=0,997.

Расчет произведите при t = 3.

При выполнении пункта 2.4. «Исследование зависимости прибыли коммерческих банков от факторных признаков» следует уяснить, что исследование объективно существующих связей между явлениями - важнейшая задача статистики. Все явления и процессы, характеризующие социально-экономическое развитие и составляющие единую систему национальных счетов, тесно взаимосвязаны и взаимозависимы.

Статистика разработала множество методов изучения связей, выбор которых зависит от цели исследования и от поставленных задач. Признаки по их значению для изучения взаимосвязи делятся на два класса. Признаки, обуславливающие изменение других, связанных с ними признаков, называются факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, являются результативными.

В статистике различают функциональную связь и стохастическую зависимость между признаками. Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Функциональная связь проявляется во всех случаях наблюдения и для каждой конкретной единицы исследуемой совокупности.

Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков. По направлению выделяют связь прямую и обратную. По аналитическому выражению выделяют связи линейные (если связь может быть приближенно выражена уравнением прямой линии) и нелинейные (связь выражается уравнением кривой линии, например, параболы, гиперболы, степенной, показательной, экспоненциальной и т.д.). Если исследуется связь между двумя признаками (результативным и факторным), то говорят о парной корреляции. Множественная корреляция - зависимость результативного и двух или более факторных признаков.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Теснота связи количественно выражается различными показателями:

0. Коэффициентом корреляции (линейная зависимость между факторами).

1. Корреляционным отношением (теоретическим или эмпирическим) в случае наличия линейной или нелинейной зависимости.

Если корреляция оценивает тесноту связи, то регрессия определяет форму статистической связи. Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой или результативным признаком) обусловлено влиянием одной или нескольких независимых величин (факторов). Регрессия может быть однофакторной (парной) и многофакторной (множественной). По форме зависимости различают линейную и нелинейную регрессию, по направлению связи - прямую и обратную.

В курсовой работе необходимо определить тип корреляционной связи между факторным и результативным признаком, исследуя зависимость графически, оценить тесноту парной корреляционной связи между результативным и факторным признаком с помощью корреляционного отношения и коэффициента корреляции, а затем определить параметры парной линейной регрессионной модели вида

,

где - подлежащие оценке параметры.

Графически взаимосвязь двух признаков изображается с помощью поля корреляции (рис.1). В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат - результативного. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.

Р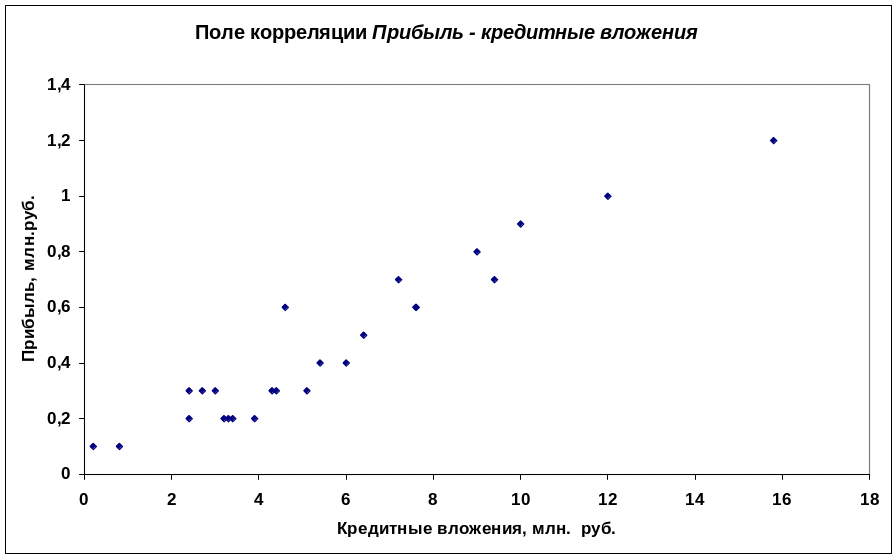 ис. 1. Поле корреляции

Измерение взаимосвязи между исследуемыми признаками (факторным и результативным) осуществляется при помощи эмпирического корреляционного отношения, которое исчисляется по формуле:

,

где - межгрупповая дисперсия результативного признака (дисперсия групповых средних).

Исчисляется она на основе данных аналитической группировки по формуле:

,

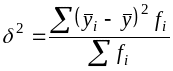где - групповая средняя результативного признака по интервалам (табл. 2 графа 8);

- общая средняя результативного признака (итог табл. 2 графа 8);

- число единиц в каждой группе.

Общая дисперсия результативного признака определяется по исходным данным по одной из формул:

а)

б) .

Теоретическое корреляционное отношение определяется по формуле

,

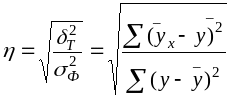где - дисперсия теоретических (выровненных) значений результативного признака, т.е. рассчитанных по уравнению регрессии;

- дисперсия эмпирических (фактических) значений результативного признака.

Линейный коэффициент корреляции вычисляется по формуле

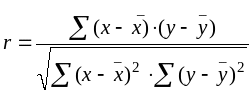
или

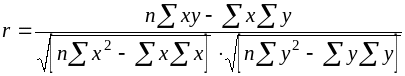
Расчет произведите по одной из указанных формул.

Параметры линейного уравнения парной регрессии определяются по формулам:

,

.

Интерпретация выходных значений коэффициента корреляции и корреляционного отношения представлена в табл. 4-5.

Таблица 4