Вопросы

1. Что понимается под статистической информацией?

2. Назовите источники информации.

3. Дайте определение статистического наблюдения. В чем его сущность?

4. Кем проводятся статистические наблюдения?

5. Какие характерные черты присущи статистическому наблюдению?

6. Какие вопросы входят в план наблюдения?

7. Что является целью наблюдения?

8. Что такое объект наблюдения и как он определяется?

9. Что представляет собой единица наблюдения?

10. Что представляет собой программа наблюдения и как она определяется?

11. В каких формах осуществляется наблюдение?

Практическое занятие № 2 Сводка и группировка статистических материалов Теоретическая часть

1. Статистическая сводка, ее содержа­ние и задачи.

2. Группировка, ее виды и принципы построения.

3. Классификация в статистике.

4. Выполнение группировки по количественному признаку.

5. Статистические ряды распределения, их виды и основные характеристики.

6. Графическое изображение дискретных и интервальных рядов распределения.

Одним из основных наиболее распространенных методов обработки и анализа первичной статистической информации является группировка.

Под группировкой понимают расчленение единиц статистической совокупности на группы, однородные в каком-либо существенном отношении, и характеристику таких групп системой показателей в целях выделения типов явлений, изучения структуры и взаимосвязей. Следовательно, с помощью группировок решаются три задачи:

• разделение всей совокупности на качественно однородные группы – выделение социально-экономических типов. Эти группировки называются типологическими (например, группировки хозяйственных объектов по формам собственности, населения по общественным группам и др.);

• характеристика структуры явления и структурных сдвигов. Эти группировки называются структурными (например, определение значения каждого вида транспорта в транспортном балансе страны, изучение состава населения по полу, возрасту и другим признакам и т.д.);

• изучение взаимосвязей между отдельными признаками изучаемого явления. Такие группировки называются аналитическими (например, группировка предприятий определенной отрасли экономики по уровню производительности труда для выявления ее влияния на себестоимость продукции).

Разделение группировок на виды является в известной мере условным. Во многих случаях одна и также группировка дает возможность решать все три задачи.

Признак, на основе которого производится подразделение единиц наблюдения на группы, называется группировочным признаком, или основанием группировки. Группировка может выполняться по одному признаку (простая группировка) и по нескольким признакам (комбинированная группировка).

Группировочные признаки могут быть атрибутивными и количественными. Атрибутивные признаки регистрируются в виде текстовой записи (например, профессия рабочих, социальная группа населения). Количественные признаки имеют цифровое выражение (стаж работы, размер дохода).

При группировке по атрибутивному признаку число групп определяется количеством соответствующих наименований, если число этих наименований не очень велико. Если признак имеет большое количество разновидностей, то при группировке ряд наименований объединяют в одну группу. Для обоснованного объединения их в группы разрабатываются классификации.

При группировке по количественному признаку число групп определяется в зависимости от характера изменения признака и задач исследования. Если количественный признак меняется прерывно (дискретно), т.е. может принимать только некоторые – чаще целые значения (например, тарифный разряд рабочих), то число групп должно соответствовать количеству значений признака.

При непрерывном изменении признак принимает любые значения (например, стаж работы или возраст рабочих), поэтому группы ограничиваются значениями признака в интервале "от – до". Интервалом называется граница между максимальным и минимальным значениями признака в каждой группе. На практике используются три вида интервалов: равные, неравные (постепенно увеличивающиеся) и специализированные.

Равные интервалы используются, если нужно охарактеризовать количественные различия в величине признака внутри групп одинакового качества (например, при группировке рабочих определенной профессии по проценту выполнения норм выработки).

Величина равного интервала исчисляется по формуле

,

где х_max, x_min – соответственно, наибольшее и наименьшее значения признака в изучаемой совокупности;

n – принятое число групп.

Для расчета величины интервала по этой формуле необходимо заранее установить число групп (при числе наблюдений более 200 используют 10-15 групп).

Оптимальное число групп может быть определено по формуле Стерджесса:

n = 1 + 3,322 lg N,

где N – число единиц совокупности.

неравные интервалы (постепенно увеличивающиеся) часто применяются в аналитических группировках. В этом случае интервалы выбираются так, чтобы число единиц в образованных группах было достаточно велико (т.е. чтобы группы были приблизительно одинаково заполнены).

Специализированные интервалы используются в типологических группировках; границы устанавливаются там, где намечается переход от одного качества к другому.

Интервалы группировки могут быть закрытыми и открытыми. Закрытые интервалы – это обычные интервалы, имеющие как нижние (т.е. "от"), так и верхние (т.е. "до") границы. Открытые интервалы – это интервалы, имеющие какую-либо одну границу – верхнюю или нижнюю.

Следующей за группировкой ступенью систематизации и обобщения материалов статистического наблюдения является статистическая сводка. Под статистической сводкой в узком смысле слова понимается подсчет числа единиц в подгруппах и группах, выделенных при группировке, и подведение итогов по количественным признакам.

Результаты группировки и сводки материалов оформляются в виде статистических таблиц.

В статистической таблице выделяются два элемента.

Подлежащее (обычно помещается в первой вертикальной или горизонтальной графе) – перечень единиц или групп, на которые подразделена вся масса единиц наблюдения.

Сказуемое – цифры, при помощи которых характеризуются выделенные в подлежащем единицы или группы.

Над таблицей помещается заголовок, отражающий в сжатой форме ее основное содержание, время и место, к которым относятся изложенные в таблице данные.

В зависимости от характера подлежащего различают три вида таблиц: простые, групповые, комбинационные.

Важным направлением в статистической сводке является построение рядов распределения, одно из назначений которых состоит в изучении структуры исследуемой совокупности, характера и закономерности распределения.

Ряд распределения – это простейшая группировка, представляющая собой распределение численности единиц совокупности по значению какого-либо признака.

Вариантами ряда распределения являются отдельные значения признака, а численности отдельных вариантов или групп ряда, показывающие, как часто встречаются те или иные варианты в ряду распределения, называют частотами.

Ряды распределения, в основе которых лежит качественный признак, называют атрибутивными. Если ряд построен по количественному признаку, его называют вариационным.

Различают дискретные (признак – целое число) и интервальные вариационные ряды (признак принимает разные значения в пределах интервала).

Анализ рядов распределения наглядно можно проводить на основе их графического изображения. Для этой цели строят полигон, гистограмму, огиву и кумуляту распределения.

Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении абсцисс и ординат точки соединяют прямыми линиями и получают ломаную линию, называемую полигоном частот (рис.1).

Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков должна быть пропорциональна частотам. В результате мы получим гистограмму-график, на котором ряд распределения изображен в виде смежных друг с другом столбиков.

Если середины верхних сторон прямоугольников соединить прямыми, то гистограмма может быть преобразована в полигон распределения (рис.1).

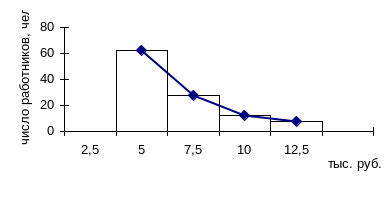
Рисунок 1. - Гистограмма и полигон распределения работников фирмы по уровню дохода.

Пример

Имеются следующие данные о стаже работы и средней месячной заработной плате рабочих – сдельщиков:

Стаж, лет	Месячная зарплата, руб., у
1	150
6	162
9	195
4	164
6	170
2	150
3	160
16	220
14	210
11	200
12	195
10	185
9	187
5	182
10	190
5	178
5	175
7	185
8	190
9	198

Для выявления зависимости между стажем работы и месячной заработной платой сгруппируйте рабочих-сдельщиков по стажу, образуя пять групп с равными интервалами. По каждой группе и в целом по совокупности рабочих подсчитайте:

1) число рабочих;

2) средний стаж работы;

3) среднемесячную заработную плату.

Результаты представьте в таблице. Дайте анализ показателей таблицы и сделайте краткие выводы.

Решение. В указанной задаче группировочным признаком является стаж работы. Образуем 5 групп с равными интервалами.

Величина равного интервала определяется по формуле:

,

где и  наибольшее и наименьшее значения группировочного признака (стаж работы);

n  число выделяемых групп (по условию задачи равно 5).

Определим величину интервала (года).

Образуем 5 групп рабочих. Нижней границей первого интервала будет минимальное значение признака (1 год), к нему добавим величину интервала (i = 3 года). Все последующие интервалы образуются аналогично. В результате получим следующие группы рабочих по стажу работы (лет):

I группа: 1 4

II группа: 4, 01  7

III группа: 7,01  10

IV группа: 10,01  13

V группа: 13,01 – 16

Распределим рабочих по группам и укажем их месячную зарплату, подсчитаем итоги по группам. Результаты группировки занесем в статистическую таблицу 1. Подлежащим в нашей таблице будут группы рабочих по стажу работы. Сказуемое таблицы показывает, какими признаками характеризуется подлежащее. Подлежащее располагается слева по строкам, сказуемое справа в графах.

Таблица 1 – Группировка рабочих по стажу работы

Группа рабочих по стажу работы, лет	Число рабочих, человек	Стаж работы, лет		Месячная з/п, руб.
		Всего	на одного рабочего	Всего	на одного рабочего
А	1	2	3	4	5
1 – 4
4,01 – 7
7,01 – 10
10,01 – 13
13,01 – 16
ИТОГО

Чтобы заполнить макет таблицы, построим вспомогательную таблицу 2 по выделенным группам. В каждой ее строке приведем показатели по рабочим, кроме того, подсчитаем итоги по группам и по всей совокупности.

Таблица 2 – Группировка рабочих по стажу работы

Группы рабочих по стажу, лет	№ рабочего по порядку	Стаж работы, лет	Месячная заработная плата, руб.
1 -4	1 2 6 7	1 4 2 3	150 164 150 160
ИТОГО	4	10	624
4.01 – 7	5 14 16 17 18 2	6 5 5 5 7 6	170 182 178 175 185 162
ИТОГО	6	34	1052
7.01 – 10	3 12 13 15 19 20	9 10 9 10 8 9	195 185 187 190 190 198
10.01 – 13	10 11	11 12	200 195
ИТОГО	2	23	395
13.01 – 16	8 9	16 14	220 210
ИТОГО	2	30	430
ВСЕГО	20	152	3646

Итоговые показатели рабочей таблицы занесем в соответствующие строки и графы макета таблицы. Рассчитаем средние показатели по этим графам (гр. 3,5). Итоговые показатели по этим графам рассчитывают аналогично расчету их по отдельным группам. После заполнения граф и строк макета получим итоговую групповую таблицу, характеризующую зависимость месячной заработной платы рабочих от стажа работы (табл. 3).

Таблица 3 – Группировка рабочих по стажу работы

Группа рабочих по стажу работы, лет	Число рабочих, человек	Стаж работы, лет		Месячная з/п, руб.
		Всего	на одного рабочего	Всего	на одного рабочего
А	1	2	3	4	5
1 – 4	4	10	2,5	624	156,0
4.01 – 7	6	34	5,6	1052	175,3
7.01 – 10	6	55	9,2	1145	190,8
10.01 – 13	2	23	11,5	395	197,5
13.01 – 16	2	30	15	430	215,0
ИТОГО	20	152	7,6	3646	182,3

Задачи

Задача 1

Имеются следующие данные результатов испытаний прочности пряжи в граммах:

200 246 227 217 232 236 212

248 209 229 219 222 239 224

243 234 225 235 220 232

1. Составьте:

а) ранжированный ряд в порядке возрастания;

б) интервальный ряд распределения, для чего данные ранжированного ряда разбейте на 4 группы с равновеликим интервалом.

2. Посчитайте в каждой группе частоты, частости, сумму накопленных частот.

3. Ряд частот представьте в виде гистограммы и полигона распределения.

Задача 2

Имеются следующие данные о сумме вкладов населения (в тыс. руб.)

20 5 40 30 60 80 20 14 10 20

25 8 12 20 90 14 8 60 43 5

12 40 24 24 120 16 11 32 45 8

25 43 60 54 36 8 44 11 62 43

на основании этих данных:

а) ранжируйте ряд в порядке возрастания;

б) составьте равновеликий интервальный ряд, выделив оптимальное число групп вкладов по формуле Стерджесса;

в) подсчитайте по каждому интервалу частоты и частости, сумму накопленных частот;

г) постройте кумуляту по накопленным частотам.

Задача 3

Пользуясь формулой Стерджесса, определите интервал группировки сотрудников отделения банка по уровню доходов, если общая численность сотрудников составляет 60 человек, а минимальный и максимальный доход соответственно равен 5000 и 50000 руб.

Задача 4

Имеются следующие данные о результатах деятельности 20 коммерческих банков одного из регионов РФ (данные условные) в млн. руб.

№ п/п	Собственный капитал	Балансовая прибыль		№ п/п	Собственный капитал	Балансовая прибыль
1	120	80		11	720	86
2	700	95		12	224	45
3	410	384		13	393	453
4	128	84		14	780	84
5	494	134		15	229	128
6	503	301		16	1193	440
7	700	378		17	496	88
8	524	411		18	886	302
9	420	93		19	437	103
10	273	393		20	905	120

Постройте аналитическую группировку коммерческих банков по величине собственного капитала, выделив четыре группы. По каждой группе определите число банков, величину собственного капитала и балансовой прибыли всего и на один банк. Результаты группировки оформите в виде таблицы и сформулируйте выводы. Укажите вид таблицы.