1.Теорема Нернста. Третій закон термодинаміки

Згідно другого закону термодинаміки, ентропія визначається як відношення кількості теплоти до температури:

,

тобто з точністю до постійного доданку, який не залежить від температури T, але може бути різним для різних тіл в стані рівноваги. Відповідні невизначені складові існують і для термодинамічних потенціалів.

1906 рік, німецький вчений Нернст на основі електротехнічних дослідів прийшов висновку, що ці доданки – універсальні і не залежать від тиску, об’єму, агрегатного стану та інших характеристик речовини. Цей новий принцип, який витікає з цих дослідів – третій закон термодинаміки, або закон Нернста.

В 1911 році Планк показав, що зміст теорії Нернста зводиться до:

1. при наближенні до абсолютного нуля, ентропія прямує до визначеної кінцевої границі. І тому є зміст казати про ентропію тіла при абсолютному нулі температур;

2. усі процеси при абсолютному нулі температур, які переводять систему з одного рівновісного в інший рівновісний стан, відбуваються без зміни ентропії.

Об’єднавши ці дві частини, маємо формулювання теореми Нернста: при наближенні до абсолютного нуля температур, приріст ентропії визначається як:

і прямує до визначеної кінцевої границі, що не залежить від значень, які приймають усі параметри, що характеризують стан системи .

Так як в термодинаміці ентропія може бути визначена з точності до довільної адитивної сталої, яка не залежить від параметрів системи, то сталу можна прийняти рівною нулю, тоді ентропію будь-якої рівновісної системи при абсолютному нулі температур можна вважати рівною нулю і тоді теорема Нернста може бути сформульована: при наближенні до абсолютного нуля, ентропія системи прямує до нуля, незалежно від того, які значення приймають усі параметри, що характеризують стан системи:

. (22)

Таким чином, відповідно до третього закону термодинаміки, ентропія системи в рівновісному стані при температурі Т може бути розрахована за допомогою рівняння:

. (23)

З третього закону термодинаміки випливає, що абсолютний нуль температур не можна досягнути ні в якому кінцевому процесі, що пов’язаний зі зміною ентропії. До нього можна лише асимптотично наближуватись.

Теорема Нернста не може бути пояснена з точки зору класичної фізики. Розглянемо приклад, пов’язаний з теплоємністю при постійному тиску (p=const), тоді:

.

Теорема Нернста потребує виконання нерівності:

.

Сходимість даного інтеграла можлива лише при умові, що температура дорівнює нулеві. Теплоємність , що протирічить висновкам класичної фізики. Аналогічно веде себе теплоємність .

2. Необернений цикл Карно

Нехай необерненість циклу обумовлена тим, що теплообмін між робочим тілом, нагрівачем та холодильником відбувається при кінцевих різницях температур нагрівача і робочого тіла. Тобто:

Необернений цикл неможливо характеризувати в будь-який момент часу заданими параметрами, але можливо деяким чином змінити параметри системи і розглянути цикл подібно до оберненого.

Так, при розширенні газу, що контактує з нагрівачем, його температура буде менше, ніж температура нагрівача, а при швидкому стисканні газу, що контактує з холодильником, температура газу в середньому буде більшою, ніж температура холодильника. Звідки випливає, що при знаходженні коефіцієнта корисної дії необерненого циклу Карно температуру необхідно замінити на температуру , а температуру - на . Тоді ККД необерненого циклу буде визначатися як:

. (5)

Можна показати, що ККД необерненого процесу майже завжди менше ніж ККД оберненого циклу Карно. Таким чином:

, (6)

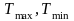- екстремальні значення температури нагрівача і холодильника, які отримали загальні назви джерел теплоти.

3.Робота А – кількісна міра енергії, яка витрачається системою для обміну із зовнішніми тілами в результаті механічної взаємодії з ними.

.

Теплота – міра енергії, якою система обмінюється з зовнішніми тілами шляхом теплопередачі без механічної роботи.

Теплоємність – відношення кількості теплоти, яка отримана тілом при нескінченно малій зміні його температури до цієї зміни:

Під питомою теплоємністю розуміють теплоємність одиниці маси речовини:

. (8)

Молярна – теплоємність 1 моля речовини:

.

.

4.Кристалічна гратка, як правило, має одночасно декілька видів симетрії.

за формою елементарної комірки всі кристали поділяють на 7 кристалографічних систем (або сингоній), кожна з яких включає в себе декілька класів симетрії.

1. Триклічна система:

.

Елементарна комірка має форму косокутного паралелепіпеда

2. Моноклінна система:

.

Пряма призма, в основі якої лежить паралелограм (тобто прямий паралелепіпед).

1. Ромбічна система:

.

Прямокутний паралелепіпед.

4. Тетрагональна система:

.

Пряма призма з квадратом в основі.

4. Ромбоедрична (тригональна) система:

.

Куб, деформований стисканням, або розтягом вздовж діагоналі.

4. Гексагональна система:

.

Якщо скласти разом три елементарні комірки, то одержимо правильну шестигранну призму.

4. Кубічна система:

.

4 типи кристалів: іонні, атомні, металічні та молекулярні.

1. іонні кристали (NaCl – кам’яна сіль). У вузлах кристалічних граток – іони різних знаків. Сили взаємодії переважно електростатичні (кулонівські).

Зв’язок обумовлений електростатичними силами притягання між різнойменно зарядженими іонами називається гетерополярним (або іонним).

2. атомні кристали (алмаз, графіт). У вузлах кристалічні гратки - нейтральні атоми.

Зв’язок, що об’єднує в кристалі (а також в молекулі) нейтральні атоми, називаються гомеополярним (або ковалентним).

Сили взаємодії при гомеополярному зв’язку також мають кулонівський характер.

Кожний іон діє на всі достатньо близькі до нього йони. Дія направлена на той атом, з яким у даного атома є спільна електронна пара.

Гомеополярний зв’язок здійснюється лише валентними (найменш зв’язаними з атомом) електронами. Оскільки кожен електрон може забезпечити зв’язок лише з одним атомом, число зв’язків, в яких може брати участь даний атом, дорівнює його валентності.

3. металічні кристали. У всіх вузлах кристалічної гратки – позитивні йони металу, між ними хаотично подібно до молекул газу, рухаються електрони, відщеплені від атомів при утворенні іонів. Ці електрони грають роль ”цементу”, утримуючи разом позитивні йони; в супротивному випадку гратка розпалася б піл дією сил відштовхування між йонами.

Разом з тим, і електрони утримуються йонами в межах гратки і не можуть її покинути.

4.молекулярні кристали. У вузлах кристалічної гратки поміщені певним чином орієнтовані молекули. Сили зв’язку між молекулами в кристалі мають ту саму природу, що й сили притягання між молекулами, яка призводять до відхилення газів від ідеальності. По цій причині, їх називають ван-дер-вальсовськими силами.

5. Плавлення і кристалізація

Перехід кристалічного тіла в рідкий стан відбувається при певній температурі для кожної речовини і потребує затрати деякої кількості тепла, що називається теплотою плавлення.

Якщо речовині, що в початковий момент знаходиться в кристалічному стані, надавати щосекунди одну і ту ж саму кількість тепла, то зміна температури з часом буде змінюватись за законом T=f(t).

Спочатку температура тіла весь час зростає. При досягненні температури плавлення (т.1), не дивлячись на те, що до тіла продовжується підвід тепла, його температура перестає змінюватись. Одночасно починається процес плавлення твердого тіла, під час якого все нові й нові порції речовини перетворюються в рідину. Після того, як процес плавлення буде завершено і вся рідина повністю перейде в рідкий стан (т.2), температура знову почне підвищуватись.

Температура плавлення залежить від тиску. На діаграмі стану (p,T) крива плавлення йде дуже круто.

Обернений плавленню процес кристалізації відбувається наступним чином: при охолодженні рідини до температури, при якій тверда і рідка фази можуть знаходитись в рівновазі при даному тиску, починається одночасний ріст кристалів навколо так званих зародків чи центрів кристалізації. Розростаючись все більше, окремі кристали врешті-решт злипаються один з одним, утворюючи полікристалічне тверде тіло.

Процес кристалізації супроводжується виділенням такої ж кількості теплоти, яка поглинається при плавленні.

6. Макроскопічні характеристики

Кожна система в будь-який момент часу знаходиться в якомусь стані. Стан цієї системи описаний за допомогою макроскопічних параметрів – макроскопічний стан або макростан.

Всі макропараметри можна розділити на:

1. внутрішні (визначають внутрішній стан системи);

2. зовнішні (характеризують зовнішні тіла і силові поля, що діють на систему).

истовується в термодинаміці.

Якщо параметр в системі довго не змінюється, то кажуть, що система у термодинамічній рівновазі.

Досліди показують, що будь-яка нерівновісна термодинамічна система, представлена сама собі, самовільно переходить в стан рівновісної системи. Самовільний процес переходу системи в рівновісний стан – релаксація, а час який витрачається на такий перехід – час релаксації.

Процеси, що складаються з неперервно послідовних станів рівноваги – квазістатичні або квазірівновісні. Такі процеси протікають досить повільно і в природі майже не існують, але ряд процесів протікає подібно до квазіврівноваженого.

Для рівновісних термодинамічних систем вводиться поняття температури як макроскопічного параметру стану, що має однакове значення для усіх макроскопічних частинок системи.