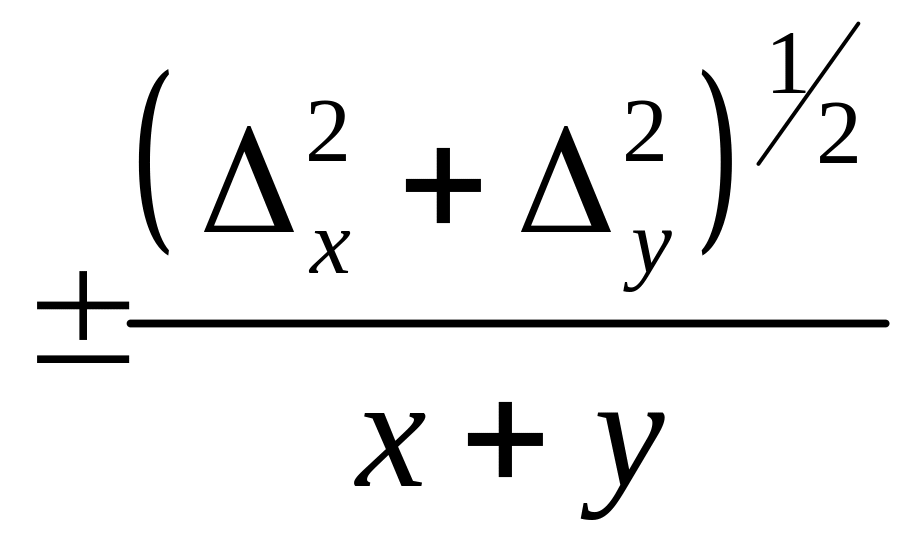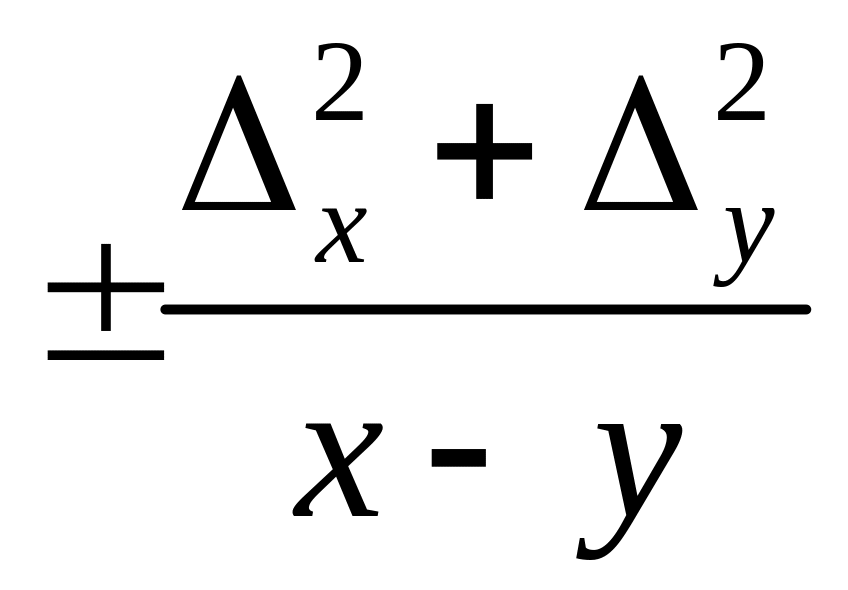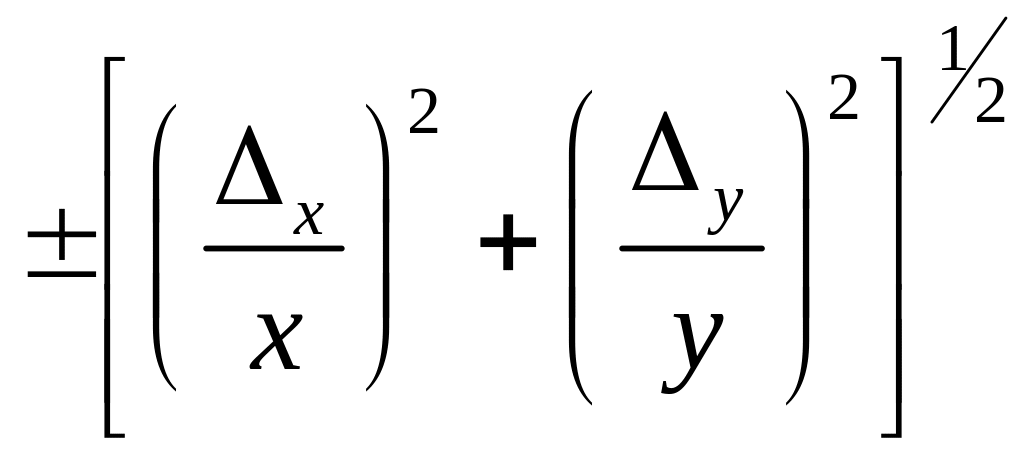1.3. Элементы теории погрешностей
В зависимости от характера проявления, причин возникновения, а также способов учёта или исключения все погрешности измерений можно разделить на три группы:
1) случайные;
2) систематические;
3) Грубые погрешности и промахи.
Случайной погрешностью называется составляющая погрешности измерений, изменяющаяся случайно при повторных измерениях одной и той же величины. Причины их возникновения и закономерности неизвестны или их невозможно учесть. Эти погрешности обусловлены случайными факторами.
Систематической погрешностью измерений называется составляющая погрешности, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Эти погрешности обусловлены факторами, которые в процессе измерений остаются постоянными или изменяются по определённому закону. Их можно учесть или исключить из результатов измерений.
Грубые погрешности - погрешности измерения, существенно превышающие ожидаемые при данных условиях. Они возникают под влиянием неожиданно сильного проявления одного из случайных факторов. Промахи связаны с неверными действиями оператора.
По причине возникновения погрешности можно разделить на инструментальные, погрешности установок, внешних влияний, методические, субъективные.
Инструментальные погрешности - обусловленны несовершенством инструментальных средств. Пример: погрешность из-за неточности нанесения делений на отсчетную шкалу, погрешность из-за люфтов и износа деталей.
Погрешность установок - возникает при работе приборов в неправильном положении или из–за несогласованности характеристик приборов, составляющих измерительную установку.
Погрешности внешних влияний появляются в связи с тем, что на работу прибора или количество меры могут оказать влияние температура окружающей среды, влажность, давление, вибрация, воздушные потоки, электрические и магнитные поля
Методические (теоретические) погрешности возникают вследствие недостаточной разработки теории метода измерения, а также от упрощений, допускаемых при проведении измерений. Пример: Подключение вольтметра с недостаточной чувствительностью (малым внутренним сопротивлением) может существенно изменить распределение токов и напряжений в исследуемой схеме.
Субъективные (личные) погрешности обусловлены индивидуальными особенностями оператора (слухом, зрением и т.д.).
Случайные погрешности
Причин, вызывающих погрешности, может быть много, а влияние каждой из них мало и изменчиво. В этом случае величина погрешности является случайной. Устранить случайные погрешности невозможно, но существуют методы их оценки, основанные на теории вероятности и математической статистике. Задача оценки погрешности результата измерения состоит в том, чтобы охарактеризовать неопределённость полученного результата, т.е. указать границы изменения погрешности результата измерения при повторных измерениях. Наиболее полной характеристикой случайной погрешности, как и любой случайной величины, является закон распределения их вероятностей, определяющий возможные значения случайной погрешности и вероятность их появления
В большинстве физических измерений случайные погрешности подчиняются закону нормального распределения - закону Гаусса.
Случайную погрешность Xi i -го результата измерении можно представить как разность между результатом измерения и математическим ожиданием М[Х] измеряемой величины, которое при отсутствии систематических погрешностей принимается за истинное значение измеряемой величины:
П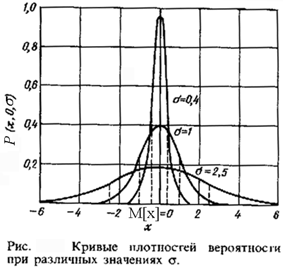 лотность
нормального распределения вероятностей
случайных погрешностей или дифференциальная
функция нормального распределения
Р(x)
выражается формулой Гаусса:
лотность
нормального распределения вероятностей
случайных погрешностей или дифференциальная
функция нормального распределения
Р(x)
выражается формулой Гаусса:
![]()
![]()
где X - случайная абсолютная погрешность; - среднеквадратическое отклонение.
Величина
2 -
дисперсия
случайной погрешности. Она представляет
собой математическое ожидание
квадрата случайной погрешности,
характеризуя разброс результатов
измерения из-за наличия случайных
погрешностей. В теории вероятности эта
величина называется вторым центральным
моментом:
![]() .
Математическое ожидание – 1-й начальный
момент:
.
Математическое ожидание – 1-й начальный
момент:
![]() .
Заметим, что математическое ожидание,
статистическим аналогом которого
является среднее арифметическое в общем
случае не равно истинному значению
измеряемой величины при конечном числе
измерений. При N
и отсутствии систематической погрешности
M[x]x0,
где x0
- истинное значение.
.
Заметим, что математическое ожидание,
статистическим аналогом которого
является среднее арифметическое в общем
случае не равно истинному значению
измеряемой величины при конечном числе
измерений. При N
и отсутствии систематической погрешности
M[x]x0,
где x0
- истинное значение.
Н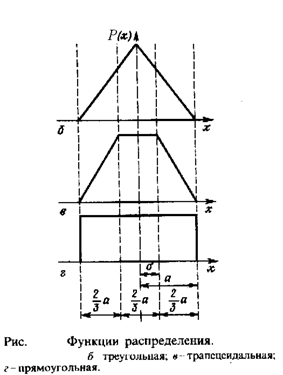 аряду
с нормальным законом распределения
случайной величины могут иметь место
и другие законы распределения: равномерный,
треугольный, трапециидальный. Примерами
случайных погрешностей с равномерным
распределением являются погрешности,
обусловленные сухим трением в опорах
стрелочного прибора, погрешности
отсчёта по равномерной шкале аналоговых
приборов, погрешности цифрового отсчёта.
Дисперсию для этих распределений можно
определить по приведенной выше формуле,
рассчитав предварительно P(x).
Для расчета P(x)
используем свойство
аряду
с нормальным законом распределения
случайной величины могут иметь место
и другие законы распределения: равномерный,
треугольный, трапециидальный. Примерами
случайных погрешностей с равномерным
распределением являются погрешности,
обусловленные сухим трением в опорах
стрелочного прибора, погрешности
отсчёта по равномерной шкале аналоговых
приборов, погрешности цифрового отсчёта.
Дисперсию для этих распределений можно
определить по приведенной выше формуле,
рассчитав предварительно P(x).
Для расчета P(x)
используем свойство
![]() .
Например, для равномерного распределения
находим, что P(x)=1/2a
в интервале
– а
x
а. Тогда
2=a2/3;
.
Например, для равномерного распределения
находим, что P(x)=1/2a
в интервале
– а
x
а. Тогда
2=a2/3;
![]() .
Аналогично можно определить, что для
треугольного закона
.
Аналогично можно определить, что для
треугольного закона
![]() .
.
Оценка погрешности результата измерения при n равноточных измерениях.
Наиболее достоверным
значением, которое можно приписать
измеряемой величине, является среднее
арифметическое значение ряда
одинаковых изменений:
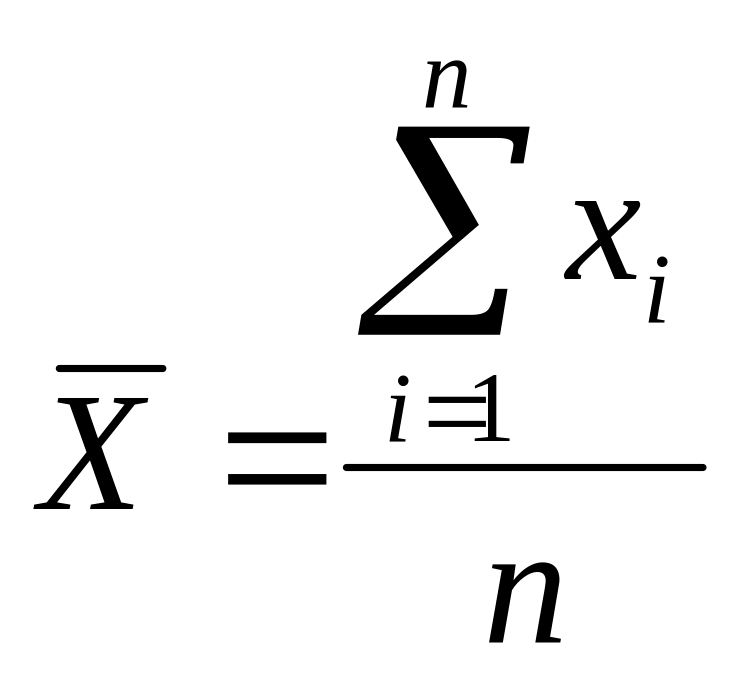
Оценкой математического
ожидания M[x]
измеряемой величины будет
![]() .
Отклонение результата каждого измерения
(по числовому значению и по знаку)
определяется из выражения
.
Отклонение результата каждого измерения
(по числовому значению и по знаку)
определяется из выражения
![]() .
Имеют место следующие свойства
.
Имеют место следующие свойства
![]() минимальна
при А= M[x].
минимальна
при А= M[x].
Приближённое
значение дисперсии определяется по
приближённой формуле Бесселя
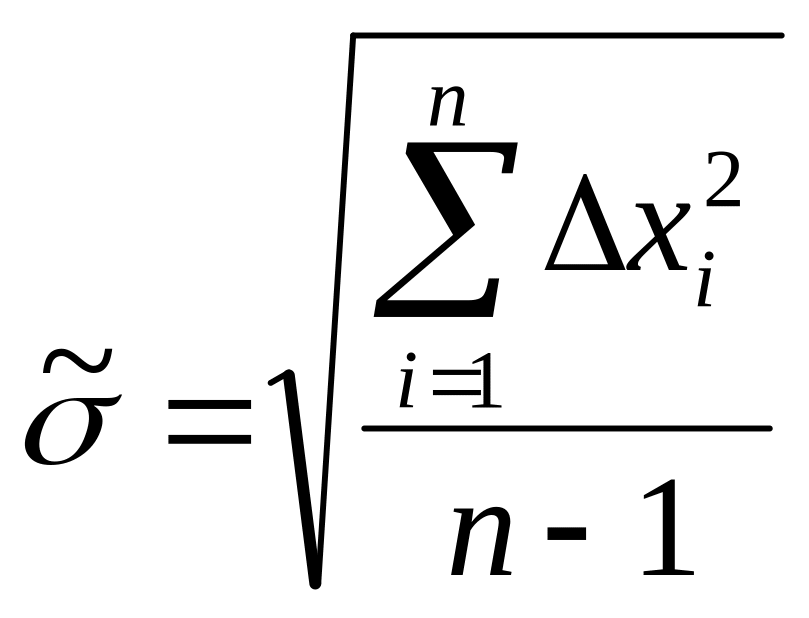 .
Оценка среднеквадратического отклонения
.
Оценка среднеквадратического отклонения
![]() характеризует точность отдельного
измерения и определяется всей совокупностью
условий измерений. Оценка
характеризует точность отдельного
измерения и определяется всей совокупностью
условий измерений. Оценка
![]() характеризует
степень рассеяния результата измерений
вокруг среднего арифметического. Так
как среднее арифметическое обладает
некоторой случайной погрешностью, то
вводится понятие оценки среднеквадратического
отклонения среднеарифметического,
равного
характеризует
степень рассеяния результата измерений
вокруг среднего арифметического. Так
как среднее арифметическое обладает
некоторой случайной погрешностью, то
вводится понятие оценки среднеквадратического
отклонения среднеарифметического,
равного
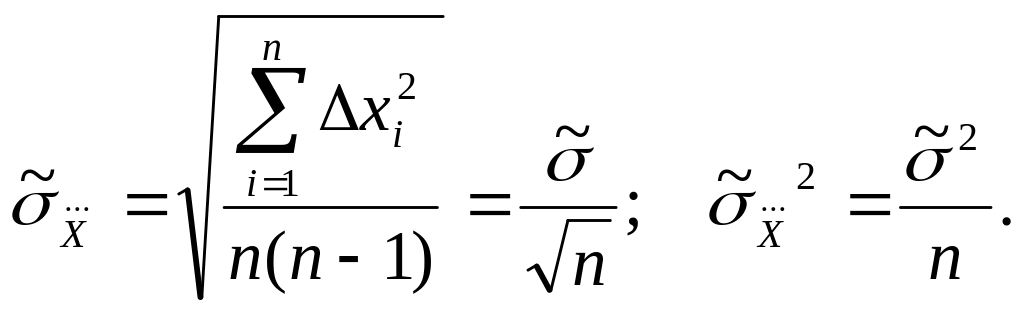
Рассмотренные оценки результата измерения, выраженные одним числом, называются точечными оценками.
Точечная оценка
погрешности измерения неполная, поскольку
![]() указывает на границы интервала, в котором
может находиться истинное значение
x0,
но ничего не говорит о вероятности
попадания x0
в этот
интервал. При интервальной оценке
определяется доверительный интервал,
между границами которого с определённой
вероятностью находится истинное значение
x0.
Вероятность
попадания случайной погрешности в
некоторый заданный интервал между 1
и 2
равна
указывает на границы интервала, в котором
может находиться истинное значение
x0,
но ничего не говорит о вероятности
попадания x0
в этот
интервал. При интервальной оценке
определяется доверительный интервал,
между границами которого с определённой
вероятностью находится истинное значение
x0.
Вероятность
попадания случайной погрешности в
некоторый заданный интервал между 1
и 2
равна
![]()
Введя замену
переменной k
= x/
для
симметричного интервала 1
= 2,
получим
![]() ,
где t
= 2/.
0Ф(t)1.
Вычисление данного интеграла позволяет
установить соответствие между значениями
Р и t.
,
где t
= 2/.
0Ф(t)1.
Вычисление данного интеграла позволяет
установить соответствие между значениями
Р и t.
-
Р
0,5
0,68
0,95
0,98
0,99
0,997
t
0,667
1
2
2,33
2,58
3
Для оценки случайных погрешностей кроме доверительного интервала [-;] иногда используют доверительный интервал [-2/3; 2/3], но чаще всего [-3;3]. При 1,2 = 2/3 (см таблицу) появление случайных погрешностей в пределах и за пределами интервала равновероятно. Вероятность появления случайных погрешностей, абсолютное значение которых более 3, составляет 0,3% (0,003). Интервал 3 в случае нормального закона представляет собой интервал достаточно достоверного результата измерения. Поэтому принято считать при практических измерениях, что появление погрешности, большей 3, почти исключено.
При
технических измерениях, когда значение
измеряемой величины определяется
при малом
числе измерений 2
n
<20, размер доверительного интервала
увеличивается и правильнее определить
его по формуле 1,2
= tp,n![]() ,
где tp,n
- коэффициент распределения Стьюдента
- зависит от задаваемой вероятности P,
числа измерений n,
и определяется по таблице, рассчитанной
на основании уравнения
,
где tp,n
- коэффициент распределения Стьюдента
- зависит от задаваемой вероятности P,
числа измерений n,
и определяется по таблице, рассчитанной
на основании уравнения
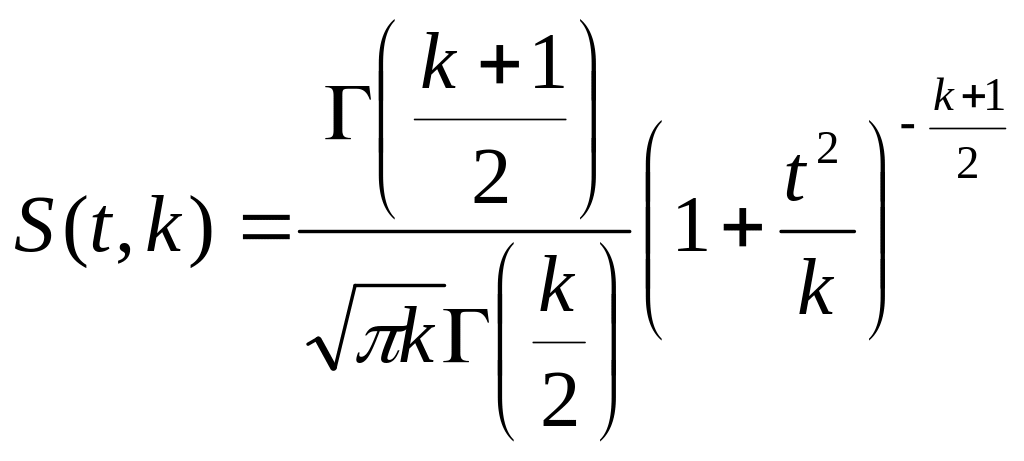 где
k
= n-1
число степеней свободы, S(t,n)
-плотность распределения Стьюдента; n
– число измерений
где
k
= n-1
число степеней свободы, S(t,n)
-плотность распределения Стьюдента; n
– число измерений
-
P
0,9
0,95
0,98
n
2
6,314
12,706
31,821
3
2,920
4,303
6.965
6
2,015
2,571
3,36
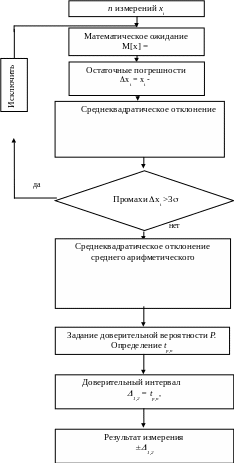
Обработка результатов измерения
Обработка результатов измерения состоит в определении приближённого значения измеряемой величины x c указанием погрешности. В случае n равноточных измерений она производится по следующему алгоритму.
Систематические погрешности,
Систематические погрешностио, делятся на постоянные и переменные. Постоянные систематические погрешности не изменяются в течение всего времени измерения.
Переменные систематические погрешности могут изменять свою величину и знак в процессе измерений по определённому закону
Обнаружение, оценка и исключение систематических погрешностей является сложной задачей метрологии.
Исключение систематических погрешностей
В любом методе измерений отсутствие тех или иных систематических погрешностей или то, что они имеют малую величину, необходимо доказать. Необнаруженная систематическая погрешность опаснее случайной, т.к. случайная погрешность может быть сведана к минимуму большим числом измерений. Поэтому при разработке новых методов измерений или новых приборов необходимо выявить и исключить систематические погрешности. Существуют следующие способы исключение систематических погрешностей
Устранение источников погрешности до начала измерений.
Исключение погрешности в процессе измерений.
Внесение поправок в результат измерений.
До начала измерения можно провести поверку прибора и его регулировку, т.е. исключить инструментальную погрешность носящую систематический характер.
Исключение погрешности в процессе измерения осуществляется двумя способами:
а) Способ замещения заключается в том, что измеряемый объект заменяется образцом, при неизменном условии проведения опыта.
б) Способ компенсации систематической погрешности по знаку заключается в том, что производится два измерения, при которых систематическая погрешность один раз входит в результат со знаком "+", а в другой раз со знаком "-". Среднее арифметическое не содержит погрешности.
Исключение систематической погрешности после измерения производится путём внесения поправок или умножения на поправочный коэффициент результата измерения. Если поправка складывается с результатом, то такая систематическая погрешность называется аддитивной (погрешность установки нуля). Если для устранения погрешности необходимо умножить результат на некоторый коэффициент, то такая погрешность называется мультипликативной (погрешность чувствительности прибора).
Часто исключить систематическую погрешность не удаётся по одной из двух причин:
1. Не с чем сравнить результат для поверки.
2. Измерение проводилось с помощью интегрирующих приборов, когда сама измеряемая величина непрерывно изменяется. В таких случаях необходимо определить границы возможных систематических погрешностей.
Погрешности средств измерений.
Различают погрешности результата измерения и погрешность самого прибора или меры. Погрешность результата измерения включает помимо погрешности прибора и другие составляющие, например, погрешность метода, субъективную погрешность. Погрешность средств измерений включают в себя обе составляющие - систематическую и случайную.
Все средства измерений, независимо от их конкретного исполнения, обладают рядом общих свойств, необходимых для выполнения ими их функционального назначения. Технические характеристики, описывающие эти свойства и оказывающие влияние на результаты и на погрешности измерений, называются метрологическими характеристиками. Перечень важнейших из них регламентируется ГОСТ 8.009—72 «ГСИ. Нормируемые метрологические характеристики средств измерений». Комплекс нормируемых метрологических характеристик устанавливается таким образом, чтобы с их помощью можно было оценить погрешность измерений, осуществляемых в известных рабочих условиях эксплуатации посредством отдельных средств измерений или совокупности средств измерений, например, автоматических измерительных систем.
Одной из основных метрологических характеристик измерительных преобразователей является статическая характеристика преобразования (иначе называемая функцией преобразования или градуировочной характеристикой). Она устанавливает зависимость у = f(х) информативного параметра у выходного сигнала измерительного преобразователя от информативного параметра х входного сигнала.
Статическая характеристика нормируется путем задания в форме уравнения, графика или таблицы некоторой номинальной статической характеристики, которая официально приписывается данному измерительному преобразователю при номинальных значениях неинформативных параметров входного сигнала. Понятие статической характеристики применимо и к измерительным приборам, если под независимой переменной х понимать значение измеряемой величины или информативного параметра входного сигнала, а под зависимой величиной y — показание прибора.
Если статическая характеристика преобразования линейна у=К х, то коэффициент К называется чувствительностью измерительного прибора (преобразователя). В противном случае под чувствительностью следует понимать производную от статической характеристики.
Важной характеристикой шкальных измерительных приборов является цена деления, т. е. то изменение измеряемой величины, которому соответствует перемещение указателя на одно деление шкалы. Если чувствительность постоянна в каждой точке диапазона измерения, то шкала называется равномерной. При неравномерной шкале нормируется наименьшая цена деления шкалы измерительных приборов, а также многозначных мер со шкалой. У цифровых приборов шкалы в явном виде нет, и для них вместо цены деления указывается цена единицы младшего разряда числа в показании прибора.
Важнейшей метрологической характеристикой средств измерений является погрешность.
Под абсолютной погрешностью меры понимается алгебраическая разность между ее номинальным Хн и действительным Хд значениями: = Хн - Хд, а под абсолютной погрешностью измерительного прибора — разность между его показанием ХП и действительным значением Хд измеряемой величины: = ХП -Хд.
Абсолютная погрешность измерительного преобразователя может быть выражена в единицах входной или выходной величины. В единицах входной величины абсолютная погрешность преобразователя определяется как разность между значением входной величины X, найденной по действительному значению выходной величины и номинальной статической характеристике преобразователя, и действительным значением Хд входной величины: = Х - Хд. Однако в большей степени точность средства измерений характеризует относительная погрешность, т. е. выраженное в процентах отношение абсолютной погрешности к действительному значению измеряемой или воспроизводимой данным средством измерений величины: = 100 X/Xд. Обычно <<1, поэтому в формулу вместо действительного значения часто может быть подставлено номинальное значение меры или показание измерительного прибора.
Если диапазон измерения прибора охватывает и нулевое значение измеряемой величины, то относительная погрешность обращается в бесконечность в соответствующей ему точке шкалы. В этом случае пользуются понятием приведенной погрешности, равной отношению абсолютной погрешности измерительного прибора к некоторому нормирующему значению XN : = 100 X/XN .
В качестве нормирующего значения принимается значение, характерное для данного вида измерительного прибора. Это может быть, например, диапазон измерений, верхний предел измерений, длина шкалы и т. д. Правила выбора нормирующего значения приводятся в ГОСТ 8.009—72.
Погрешности измерительных средств принято подразделять на статические, имеющие место при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей, и динамические, появляющиеся при измерении переменных величин и обусловленные инерционными свойствами средств измерений.
Согласно общей классификации, статические погрешности измерительных средств делятся на систематические и случайные. Систематические погрешности являются в общем случае, функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени.
В функции измеряемой величины систематические погрешности находят при поверке и аттестации образцовых приборов, например, измерением наперед заданных значений измеряемой величины в нескольких точках шкалы. В результате строится кривая или создается таблица погрешностей, которая используется, для определения поправок. Поправка в каждой точке шкалы численно равна систематической погрешности и обратна ей по знаку, поэтому при определении действительного значения измеряемой величины поправку следует прибавить к показанию прибора. Так, если поправка к показанию динамометра 120 Н равна +0,6 Н, те действительное значение измеряемой силы составляет 120 + 0,6 = 120,6 Н. Удобнее пользоваться поправкой, чем систематической погрешностью, поэтому приборы чаще снабжают кривыми или таблицами поправок.
Систематическую погрешность в функции измеряемой величины можно представить в виде суммы погрешности схемы, определяемой самой структурной схемой средства измерений, и технологических погрешностей, обусловленных погрешностями изготовления его элементов.
Как те, так и другие виды погрешностей можно рассматривать в качестве систематических лишь при измерении постоянной величины с помощью одного экземпляра измерительного прибора. В массе же измерений различных значений физической величины, осуществляемых одним или многими приборами того же типоразмера, эти систематические погрешности приходится относить к классу случайных.
Выделение систематических погрешностей в отдельную группу обусловливается, таким образом, лишь тем, что при поверке измерительных средств они могут быть определены для каждой точки шкалы и исключены из результатов последующих измерений. Именно так и поступают при точных метрологических измерениях.
Между погрешностями схемы и технологическими погрешностями средств измерений существует принципиальная разница. Если первые накладывают свой отпечаток на характер изменения по шкале суммарной погрешности всех средств измерений - данного типоразмера, то технологические погрешности индивидуальны - для каждого экземпляра, т. е. их значения в одних и тех же точках шкалы различны для различных экземпляров приборов. Этим, конечно, не отрицается возможность существования вероятностных связей между ними как в одной, так и в нескольких точках шкалы, поскольку общность технологического процесса изготовления приборов данного типа, несомненно, создает некоторую общность изменения их технологических погрешностей.
К числу характеристик погрешности относится также вариация выходного сигнала измерительного преобразователя или вариация показаний измерительного прибора. Согласно ГОСТ 8.009—72 вариацией называется средняя разность между значениями информативного параметра выходного сигнала измерительного преобразователя (или показаний измерительного прибора), соответствующими данной точке диапазона измерений при двух направлениях медленного многократного изменения информативного параметра входного сигнала в процессе подхода к данной точке диапазона. Вариация возникает из-за трения и зазоров в сочленениях подвижных деталей механизмов средств измерений или гистерезисных явлений, свойственных его элементам.
Динамические погрешности обусловливаются инерционными свойствами средств измерений и появляются при измерении переменных во времени величин. Типичным случаем является измерение с регистрацией сигнала, изменяющегося со временем. Если x(t) и y(t) — сигналы на входе и на выходе средства измерений с чувствительностью К, то динамическая погрешность определяется как Д = y(t)/K - x(t).
Для средств
измерений, являющихся линейными
динамическими системами с
сосредоточенными, постоянными во времени
параметрами, наиболее общая
характеристика динамических свойств
— это дифференциальное уравнение. В
этом случае уравнение линейное с
постоянными коэффициентами:
![]() ,
где y(i)(t)
и
x(j)(t)
- i-е
и j-е
производные входного и выходного
сигналов; аi
и bj,
-- постоянные
коэффициенты, n
и m
— порядок левой и правой частей уравнения,
причем n
> m.
,
где y(i)(t)
и
x(j)(t)
- i-е
и j-е
производные входного и выходного
сигналов; аi
и bj,
-- постоянные
коэффициенты, n
и m
— порядок левой и правой частей уравнения,
причем n
> m.
Дифференциальное уравнение является метрологической характеристикой средств измерения, поскольку позволяет при известном сигнале на входе x(t) найти выходной сигнал у(t) и после подстановки их в соответствующее выражение вычислить динамическую погрешность.
Для нормирования динамических свойств средств измерения часто указывают не само дифференциальное уравнение, а другие, производные от него, динамические характеристики, которые более просто находятся экспериментальным путем. Сюда относятся передаточная функция, амплитудная и фазовая частотные характеристики, переходная и импульсная переходная функции.
К числу метрологических характеристик средств измерения относятся и не информативные параметры выходного сигнала измерительного преобразователя или меры, поскольку они могут оказывать существенное влияние на погрешность средства измерений. Например, непостоянство амплитуды колебаний баланса наручных часов (неинформативный параметр) приводит к изменению частоты его колебаний (информативный параметр).
При восприятии измеряемой величины или измерительного сигнала средство измерения оказывает некоторое воздействие на объект измерения или на источник сигнала. Результатом этого воздействия может быть некоторое изменение измеряемой величины относительно того значения, которое имело место при отсутствии средства измерения. Такое обратное воздействие средства измерения на объект измерения особенно четко просматривается при измерении электрических величин.
Так, ЭДС нормального элемента определяется как напряжение на его зажимах в режиме холостого хода. При измерении этого напряжения вольтметром с некоторым конечным входным сопротивлением результат измерения будет зависеть от соотношения между внутренним сопротивлением нормального элемента (его выходное сопротивление) и входным сопротивлением вольтметра. Для оценки возникающей при этом погрешности необходимо знать значения этих сопротивлении, поэтому их следует рассматривать как метрологические характеристики меры (нормальный элемент) и измерительного прибора (вольтметр). В более сложных случаях эти сопротивления могут быть комплексными, и тогда носят общее название входного и выходного импеданса. Для средств измерения неэлектрических величин под входным импедансом понимается отношение обобщенной силы, действующей на входе измерительного прибора или преобразователя, к обобщенной скорости, действующей во входной цепи. Обобщенная сила и скорость выбираются при этом, как две взаимодействующие величины, одна из которых является измеряемой, а их произведение образует мощность.
Так, для вольтметра измеряемой величиной является напряжение (обобщенная сила), тогда обобщенной скоростью должна быть сила тока. Их отношение и есть сопротивление. При измерений силы пружинным динамометром эта сила является обобщенной силой, а в качестве обобщенной скорости следует, рассматривать скорость деформации упругого элемента под действием этой силы. Их отношение образует входной импеданс динамометра. Однако для средств измерений неэлектрических величин импедансы пока еще, как правило, непосредственно не нормируются. Вместо них в научно-технической документации приводятся другие характеристики, описывающие меру воздействия средства измерений на объект измерений, например, измерительное усилие для средств измерений перемещений.
Таким образом, метрологическими характеристиками, описывающими взаимодействие средств измерений друг с другом или с объектом измерений, являются: выходной импеданс мер; входной и выходной импеданс измерительных преобразователей; входной импеданс измерительных приборов.
Влияние внешних воздействий и неинформативных параметров сигналов (влияющих величин) описывается с помощью метрологических характеристик, называемых функциями влияния. Функция влияния (1; 2; ...; q) —это зависимость соответствующей метрологической характеристики из числа вышеперечисленных от влияющих величин 1; 2; ...; q (температуры внешней среды, параметров внешних вибраций и т. д.). В большинстве случаев можно ограничиваться набором функций влияния каждой из влияющих величин (1); (2); (q), но иногда приходится использовать функции совместного влияния нескольких величин, если изменение одной из влияющих величин приводит к изменению функции влияния другой.
Для средств измерений, не входящих в более сложные комплексы и обладающих точностью, заведомо превышающей требуемую точность измерений, вместо функций влияния указывают наибольшие допустимые изменения метрологических характеристик l(), вызванные изменениями внешних влияющих величин и неинформативных параметров входного сигнала. Это связано с тем, что при использовании таких средств измерений обычно не вводятся поправки на влияющие величины и специально не рассчитываются границы погрешности.
Под нормированием метрологических характеристик понимается установление границ на допустимые отклонения реальных метрологических характеристик средств измерений от их номинальных значений. Только посредством нормирования метрологических характеристик средств измерений можно добиться их взаимозаменяемости и обеспечить единство измерений в государстве. Реальные значения метрологических характеристик определяют при изготовлении средств измерений и затем проверяют периодически во время эксплуатации. Если при этом хотя бы одна из метрологических характеристик выходит за установленные границы, то такое средство измерений либо подвергают регулировке, либо изымают из обращения.
Нормы на значения метрологических характеристик устанавливаются стандартами на отдельные виды средств измерения. При этом делается различие между нормальными и рабочими условиями применения средств измерения.
Нормальными считаются такие условия применения средств измерений, при которых влияющие на процесс измерения факторы (температура, влажность, частота, напряжение питания, внешние магнитные поля и т. д.), а также неинформативные параметры входных и (или) выходных сигналов, находятся в нормальной для данных средств измерений области значений, т. е. в такой области, где их влиянием на метрологические характеристики можно пренебречь. Нормальные области значений влияющих факторов указываются в стандартах или технических условиях на средства измерений данного вида в форме номиналов с нормированными отклонениями, например, температура должна составлять (20±2) °С, напряжение питания —(220 В±10%) или в форме интервалов значений (влажность 30—80 %).
Рабочая область значений влияющих факторов шире нормальной области значений. В ее пределах метрологические характеристики существенно зависят от влияющих факторов, однако, их изменения нормируются стандартами на средства измерений в форме функций влияния или наибольших допустимых изменений. За пределами рабочей области метрологические характеристики принимают неопределенные значения.
Для нормальных условий эксплуатации средств измерений должны нормироваться характеристики суммарной погрешности и ее систематической и случайной составляющих, входной импеданс измерительных приборов и преобразователей, выходной импеданс преобразователей, динамические характеристики и неинформативные параметры выходного сигнала.
Суммарная погрешность средств измерений в нормальных условиях эксплуатации называется основной погрешностью и нормируется заданием предела допускаемого значения д, т. е. того наибольшего значения, при котором средство измерений еще может быть признано годным к применению.
Систематическая составляющая погрешности с становится случайной при рассмотрении всего ансамбля средств измерений данного типа. Поэтому она подлежит нормированию путем задания предела сд допускаемой систематической погрешности и её двух числовых характеристик — математического ожидания М[с] и среднего квадратического отклонения [с] систематической погрешности с средств измерений данного тина.
Случайная составляющая погрешности нормируется путем задания предела д[] среднего квадратического отклонения д[], поскольку ее математическое ожидание равно нулю.
Вариация b показаний измерительного прибора так же, как и вариация выходного сигнала измерительного преобразователя, нормируются заданием предела bд допускаемого значения вариации средств измерения данного типа.
Все характеристики погрешности могут выражаться в форме абсолютных, относительных или приведенных погрешностей как функции измеряемой величины или информативного параметра входного сигнала в виде формул, графиков или таблиц.
Неинформативные параметры выходного сигнала, а также входной zвх и выходной zвых импедансы нормируются своими номинальными значениями и наибольшими допустимыми отклонениями в единицах нормируемого параметра или в процентах от его номинального значения.
Перечисленные выше метрологические характеристики следует нормировать не только для нормальной, но и для всей рабочей области эксплуатации средств измерения, если их колебания, вызванные изменениями внешних влияющих факторов и неинформативных параметров входного сигнала в пределах рабочей области, существенно меньше номинальных значений. В противном случае эти характеристики нормируются только для нормальной области, а в рабочей области нормируются дополнительные погрешности путем задания функций влияния () или наибольших допустимых изменений l() раздельно для каждого влияющего фактора , а в случае необходимости и для совместного изменения нескольких факторов. Функции влияния нормируются формулой, числом, таблицей или задаются в виде номинальной функции влияния и предела допускаемых отклонений от нее. Наибольшие допускаемые изменения указываются в виде зоны в единицах дайной метрологической характеристики или в процентах от ее значения, нормированного для нормальных условий.
Для различных по назначению и свойствам средств измерений могут нормироваться не все вышеперечисленные метрологические характеристики, а только некоторые из них.
Для средств измерений, используемых только по отдельности, не подлежит нормированию статическая функция преобразования, выходной импеданс и неинформативные параметры выходного сигнала, поскольку эти характеристики не существенны для средств измерения данной группы. Однако для средств измерения, входящих в сложные измерительные комплексы, эти характеристики описывают эффекты их взаимодействия и поэтому должны нормироваться государственными стандартами. Можно не нормировать и случайную составляющую суммарной погрешности, если она существенно меньше систематической, причем признак существенности должен устанавливаться стандартами технических требований для данного типа средств измерений.
Для используемых по отдельности средств измерений, точность которых заведомо превышает требуемую точность измерений, нормируются только пределы д допускаемого значения суммарной погрешности и наибольшие допустимые изменения метрологических характеристик. Если же точность средств измерений соизмерима с требуемой точностью измерений, то необходимо нормировать раздельно характеристики систематической и случайной погрешности и функции влияния. Только с их помощью можно найти суммарную погрешность в рабочих условиях применения средств измерений.
Динамические характеристики нормируются путем задания номинального дифференциального уравнения или передаточной, переходной или импульсной переходной функции для средств измерений, предназначенных для работы в комплексе с другими, например, в измерительных системах, или в форме графиков или таблиц номинальных амплитудно - и фазочастотных характеристик и времени установления показаний для всех прочих средств измерении. Одновременно нормируются наибольшие допустимые отклонения динамических характеристик от номинальных.
Класс точности — это обобщенная характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений. Классы точности регламентируются стандартами на отдельные виды средств измерения с использованием метрологических характеристик и способов их нормирования, изложенных выше.
Способы установления классов точности изложены в ГОСТ 8.401—80 «ГСП. Классы точности средств измерения. Общие требования». Стандарт не распространяется на средства измерений, для которых предусматриваются раздельные нормы на систематическую и случайные составляющие, а также на средства измерений, для которых нормированы номинальные функции влияния, а измерения проводятся без введения поправок на влияющие факторы. Классы точности не устанавливаются и на средства измерений, для которых существенное значение имеет динамическая погрешность.
Для остальных средств измерений обозначение классов точности вводится в зависимости от способов задания пределов допускаемой основной погрешности.
Пределы допускаемой абсолютной основной погрешности могут задаваться либо в виде одночленной формулы = a, либо в виде двухчленной формулы = (а+bх), где и х выражаются одновременно либо в единицах измеряемой или воспроизводимой мерой величины, либо в делениях шкалы измерительного прибора.
Более предпочтительным является задание пределов допускаемых погрешностей в форме приведенной или относительной погрешности.
Пределы допускаемой приведенной основной погрешности нормируются в виде одночленной формулы = /XN = p, где число р выбирается из ряда р=1*10n; 1,5*10n; 2*10n; 2,5*10n; 4*10n; 5*10n; 6*10n (n=1; 0; —1; —2 и т. д.).
Пределы допускаемой относительной основной погрешности могут нормироваться либо одночленной формулой = /x = q, либо двухчленной формулой = / x = [c+d(Xk/X -1)],
где Xk - конечное значение диапазона измерений или диапазона значений воспроизводимой многозначной мерой величины, а постоянные числа q, c и d выбираются из того же ряда, что и число р.
В обоснованных случаях пределы допускаемой абсолютной или относительной погрешности можно нормировать по более сложным формулам или даже в форме графиков или таблиц в зависимости от значения измеряемой, входной или воспроизводимой мерой величины.
Способ задания пределов допускаемой основной погрешности измерительных преобразователей и приборов определяется главным образом зависимостью погрешности от измеряемой или соответственно входной величины.
Таким образом, в настоящее время существуют три способа нормирования основной погрешности измерительных приборов и преобразователей:
а) нормирование заданием пределов допускаемой основной абсолютной или приведенной погрешности ± или ± , постоянных во всем диапазоне измерения или преобразования;
б) нормирование заданием пределов допускаемой основной абсолютной или относительной погрешности ± или ± в функции измеряемой величины по формулам;
в) нормирование заданием постоянных пределов допускаемой основной погрешности, различных для всего диапазона измерения и одного или нескольких нормированных участков, или различных для разных диапазонов измерения (для многопредельных приборов).
Первый способ широко применяется для нормирования основной погрешности большинства сравнительно узкопредельных стрелочных измерительных приборов, а также для измерительных преобразователей. Остальные два способа отвечают в большей степени условиям измерения, имеющим место при использовании широкопредельных приборов.
С редствам
измерений, пределы допускаемой основной
погрешности которых задаются
относительной погрешностью по одночленной
формуле, присваивают классы точности,
выбираемые из ряда чисел р
и равные соответствующим пределам в
процентах. Так для средства измерений
с
= 0,002 класс точности обозначается .
редствам
измерений, пределы допускаемой основной
погрешности которых задаются
относительной погрешностью по одночленной
формуле, присваивают классы точности,
выбираемые из ряда чисел р
и равные соответствующим пределам в
процентах. Так для средства измерений
с
= 0,002 класс точности обозначается .
Если пределы допускаемой основной относительной погрешности выражаются двухчленной формулой, то класс точности обозначается как c/d, где числа с и d выбираются из того же ряда, что и р, но записываются в процентах. Так, измерительный прибор класса точности 0,02/0,01 характеризуется пределами допускаемой основной относительной погрешности
= ± [0,0002 +0,0001( Xk/X -1)] = ± [0,02 +0,01( Xk/X -1)]%.
К лассы
точности средств измерений, для которых
пределы допускаемой основной
приведенной погрешности нормируются
по формуле для ,
обозначаются одной цифрой, выбираемой
из ряда для чисел р
и выраженной в процентах. Если, например,
= ±0,005= ±0,5 %, то класс точности обозначается
как 0,5 (без кружка), если нормирующее
значение выражается в единицах входной
или выходной величины, или как , если
нормирующее значение принято равным
длине всей шкалы или длине какого-либо
ее интервала.
лассы
точности средств измерений, для которых
пределы допускаемой основной
приведенной погрешности нормируются
по формуле для ,
обозначаются одной цифрой, выбираемой
из ряда для чисел р
и выраженной в процентах. Если, например,
= ±0,005= ±0,5 %, то класс точности обозначается
как 0,5 (без кружка), если нормирующее
значение выражается в единицах входной
или выходной величины, или как , если
нормирующее значение принято равным
длине всей шкалы или длине какого-либо
ее интервала.
Классы точности обозначаются римскими цифрами или буквами латинского алфавита для средств измерений, пределы допускаемой погрешности которых задаются в форме графиков, таблиц или сложных функции входной, измеряемой или воспроизводимой величины. К буквам при этом допускается присоединять индексы в виде арабской цифры. Чем меньше пределы допускаемой погрешности, тем ближе к началу алфавита должна быть буква и тем меньше цифра. Недостатком такого обозначения класса точности является его чисто условный характер.
Наряду с основной погрешностью для средств измерений, поделенных на классы точности, нормируются и пределы допускаемых дополнительных погрешностей в виде дольного или кратного значения основной погрешности раздельно для каждой влияющей величины.
Пределы допускаемых дополнительных погрешностей могут выражаться в соответствии с ГОСТ 8.401—80 в форме постоянных значений для всей рабочей области влияющей величины или в виде постоянных значений по интервалам рабочей области; отношением предела допускаемой дополнительной погрешности к интервалу значений влияющей величины; путем указания предельной функции влияния, то есть зависимости предела допускаемой дополнительной погрешности от значения соответствующей влияющей величины.
Следует отметить, что никакое нормирование погрешностей средств измерений само по себе не может обеспечить единства измерений. Для достижения единства измерений необходима регламентация самих методик проведения измерений, чему посвящен ГОСТ 8.010—72 «Государственная система обеспечения единства измерений. Общие требования к стандартизации и аттестации методик проведения измерений». Последовательное внедрение этого стандарта является важным шагом на пути достижения действительного единства измерений в стране.
Погрешности косвенных измерений
Результат косвенных
измерений
![]() (1)
(1)
Если известны
числовые характеристики погрешностей
измерений
![]() ,
т.е. известны
,
т.е. известны
![]() (i-полная
погрешность, ci
–систематическая погрешность,
(i-полная
погрешность, ci
–систематическая погрешность,![]() -
случайная погрешность
),
то можно определить погрешности
-
случайная погрешность
),
то можно определить погрешности
![]() измерения
измерения
![]() .
Для этого представим выражение (1) в виде
степенного ряда:
.
Для этого представим выражение (1) в виде
степенного ряда:
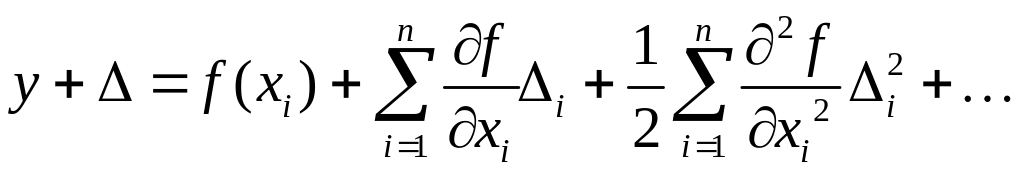
Так как погрешности
малы по сравнению со значением измеренной
величины, то в разложении можно пренебречь
слагаемыми со степенями
![]() выше первой и учитывая (1):
выше первой и учитывая (1):
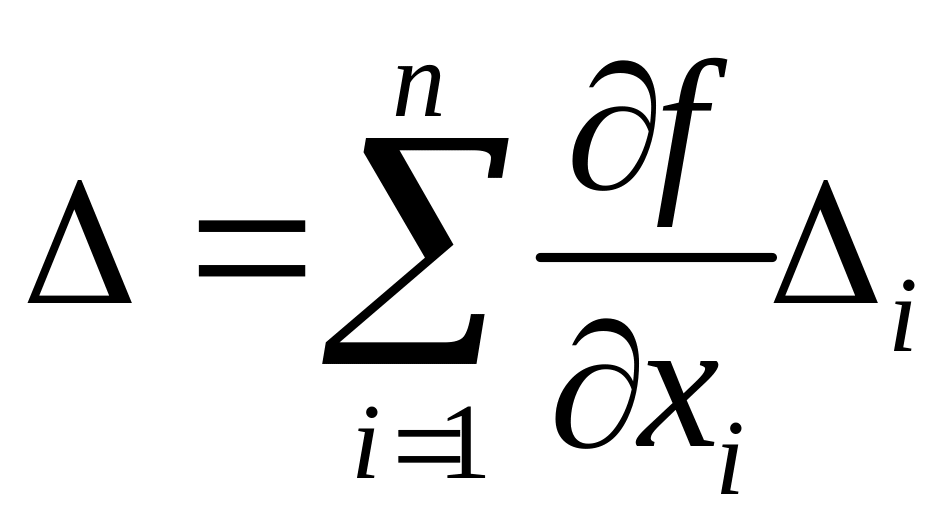 (2)
(2)
Систематическая
погрешность представляет собой
математическое ожидание
![]() ,
учитывая, что математическое ожидание
суммы равно сумме математических
ожиданий, получаем:
,
учитывая, что математическое ожидание
суммы равно сумме математических
ожиданий, получаем:
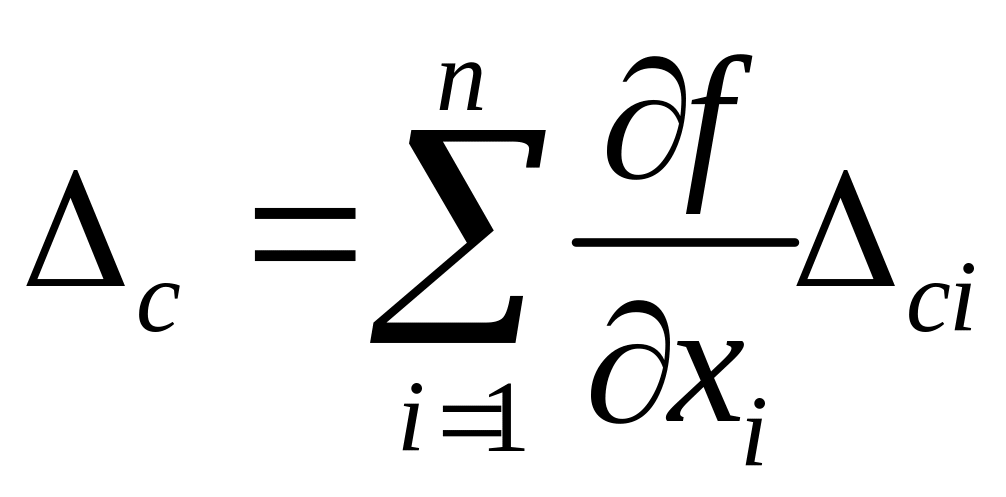 (3)
(3)
Это справедливо лишь при учете 1-х степеней, при учете уже 2-х степеней, появляются зависимости от , т.е. от случайной погрешности.
Вычитая (3) из (2), получим
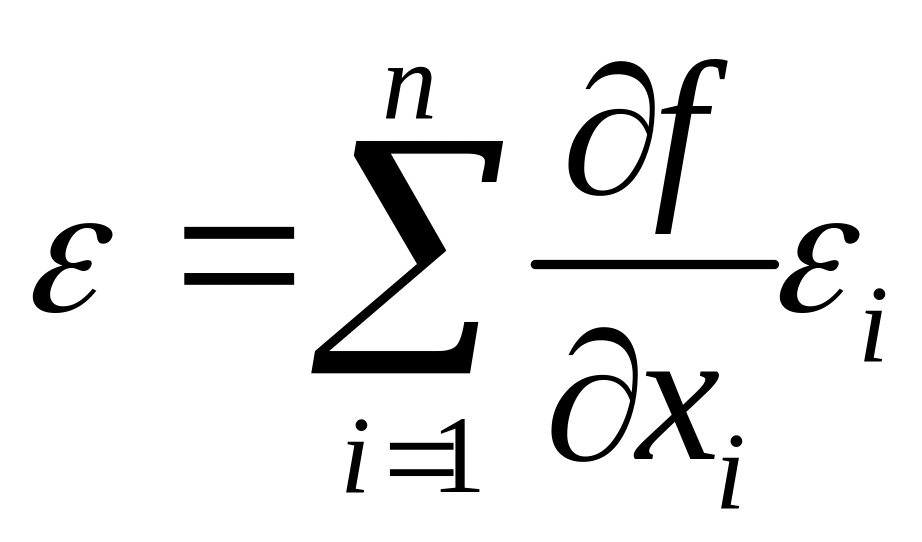 .
.
Возведем обе части уравнения в квадрат:
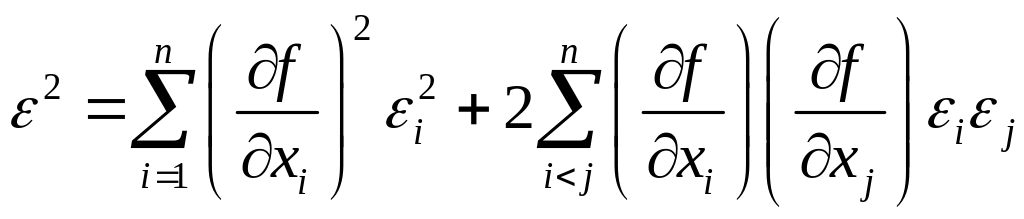 это точная формула
квадрата суммы.
это точная формула
квадрата суммы.
Вычислив математическое ожидание левой и правой частей равенства, получим с учетом:
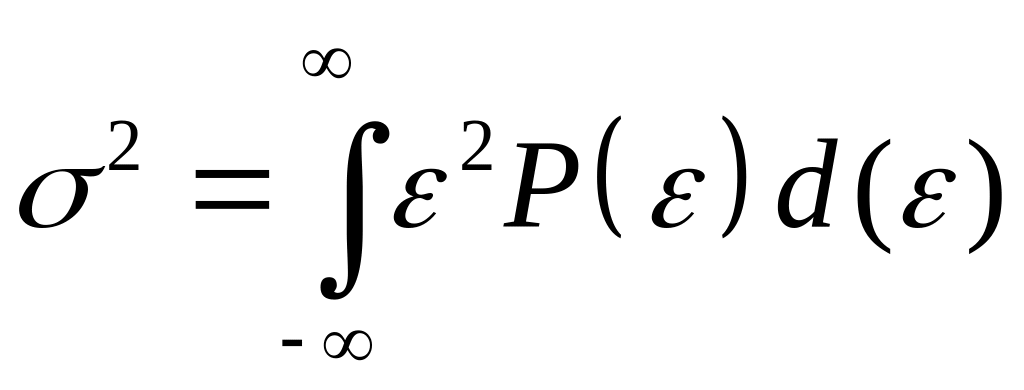 ,
,
 ,
,
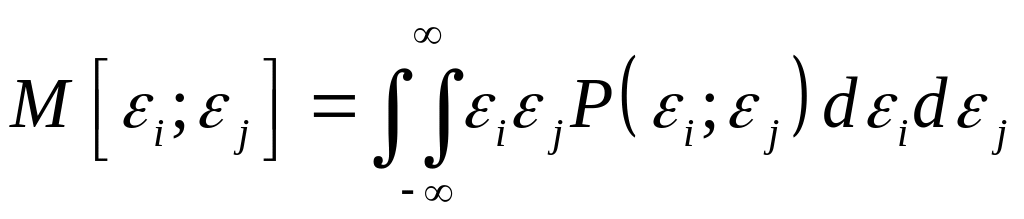
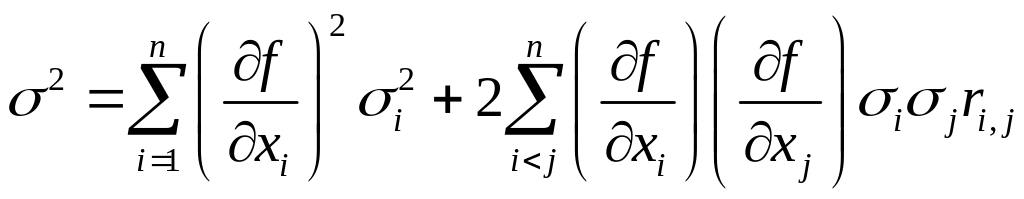 , (4)
, (4)
где
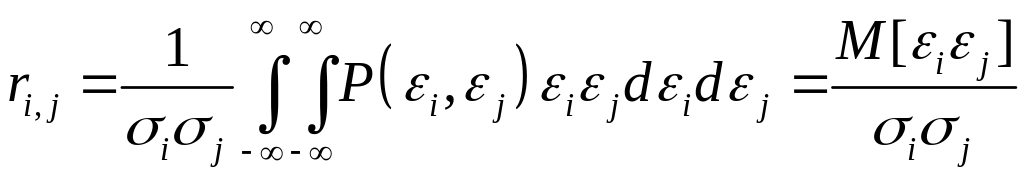 – коэффициент взаимной корреляции
погрешностей,
– коэффициент взаимной корреляции
погрешностей,
![]() - совместная плотность вероятности
случайных величин
и
- совместная плотность вероятности
случайных величин
и
![]() .
.
Коэффициент
взаимной корреляции
![]() характеризует статистическую связь
погрешностей и заключен в пределах ±1.
Предельные значения
соответствуют линейной связи
и
.
Для статистически независимых погрешностей
характеризует статистическую связь
погрешностей и заключен в пределах ±1.
Предельные значения
соответствуют линейной связи
и
.
Для статистически независимых погрешностей
![]() .
.
Для статистически независимых погрешностей
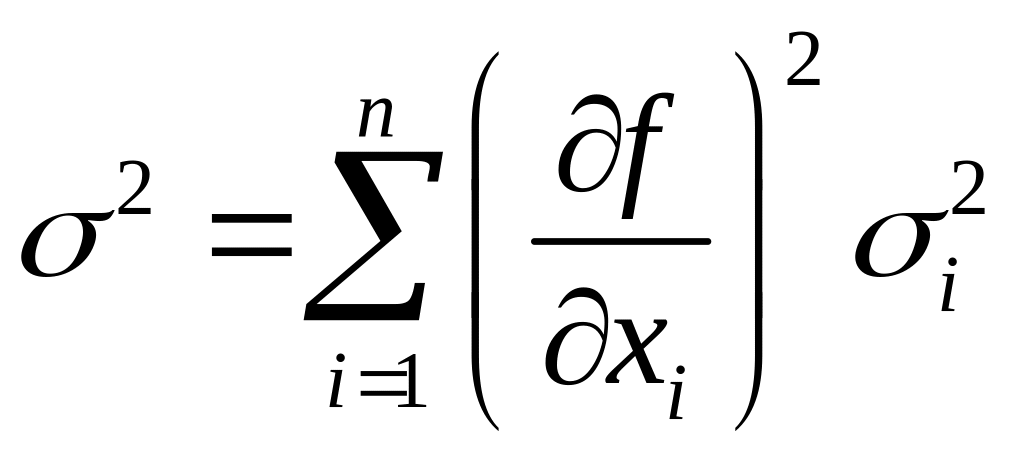 .
.
На практике обычно
информация о степени корреляционной
связи отсутствует, и рассматривают
![]() .
.
Погрешность суммы
Пусть зависимость
от
имеет
вид суммы
 .
В этом случае
.
В этом случае
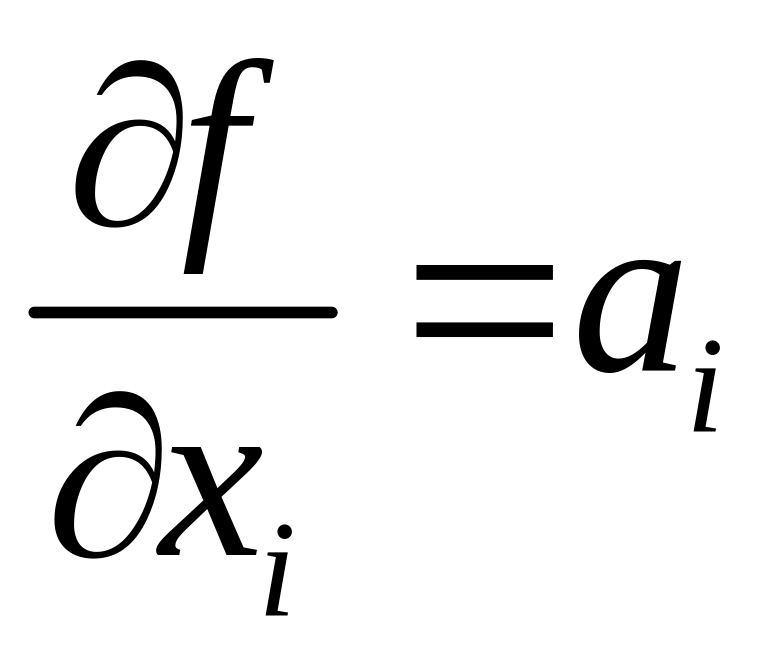 и выражения для погрешностей имеют вид:
и выражения для погрешностей имеют вид:
 ,
,
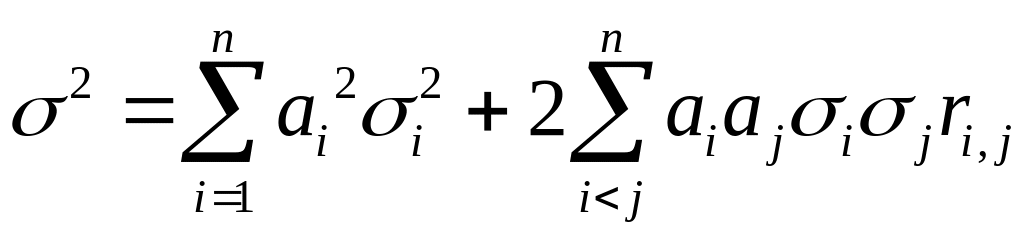 .
.
Погрешность произведения
Рассмотрим функцию
вида
![]() ,
,
![]() В этом случае
В этом случае
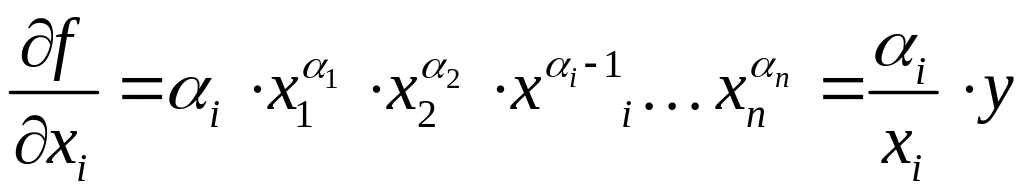 ,
,
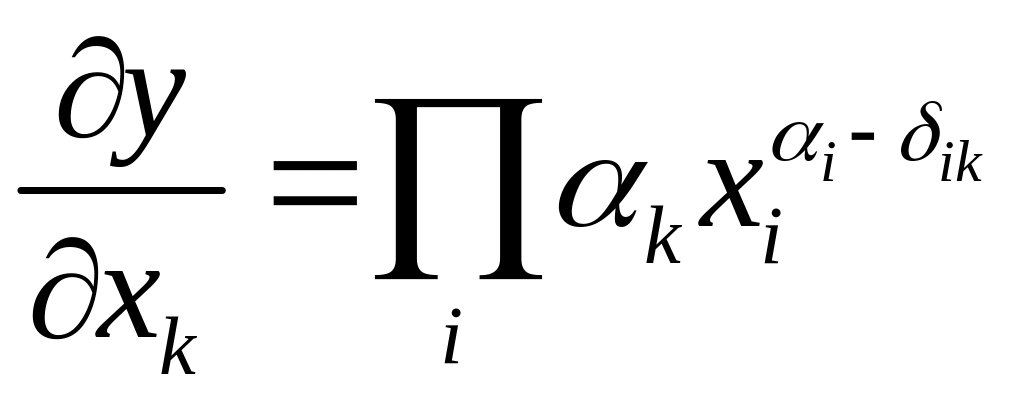 .
Подставив эти выражения в (3) и разделив
обе части на
,
получим:
.
Подставив эти выражения в (3) и разделив
обе части на
,
получим:
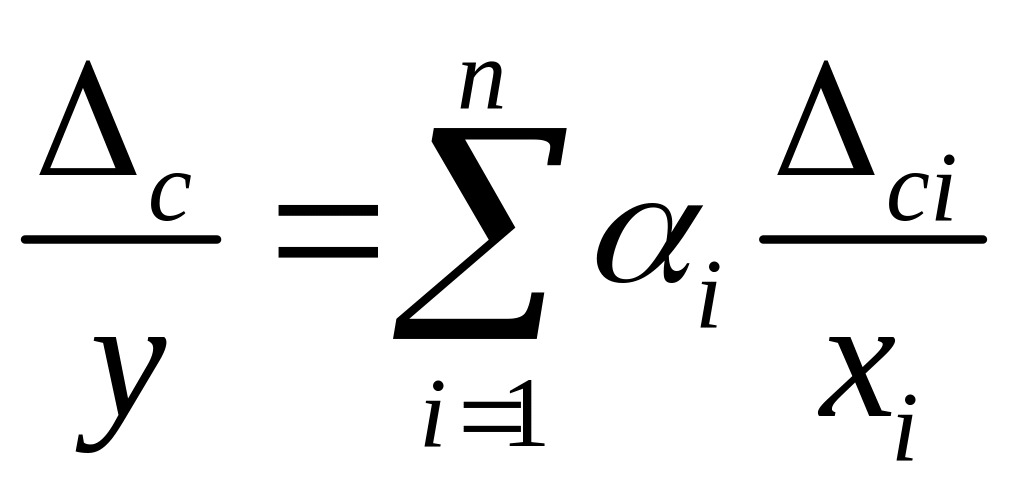 .
.
Из (4) получим выражение для среднеквадратических отклонений:
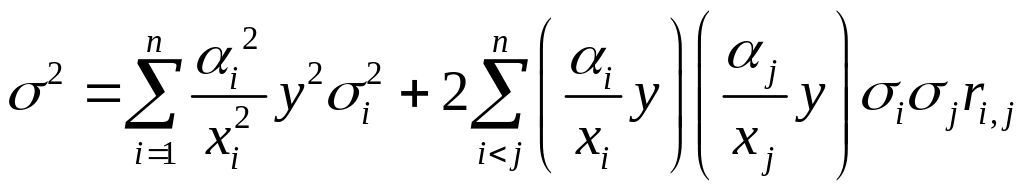 .
.
Поделив обе части
уравнения на
![]() ,
получим:
,
получим:
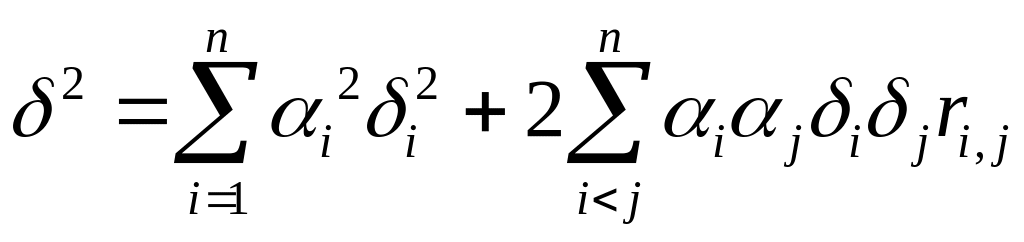 ,
,
Где
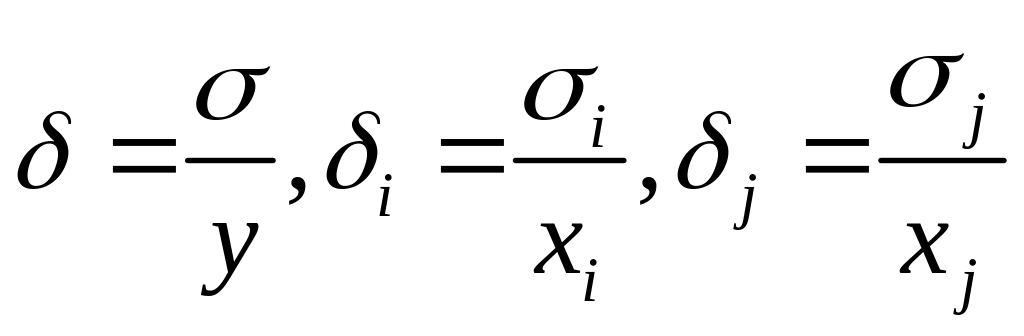 - относительные средние квадратичные
отклонения результатов измерений
и
.
- относительные средние квадратичные
отклонения результатов измерений
и
.
Примеры вычисления
погрешностей для некоторой
![]()
Так как предельные
погрешности находятся через
![]() :
:
|
|
|
|
|
|
|
|
|
При ограниченном числе измерений формула для приобретает вид:
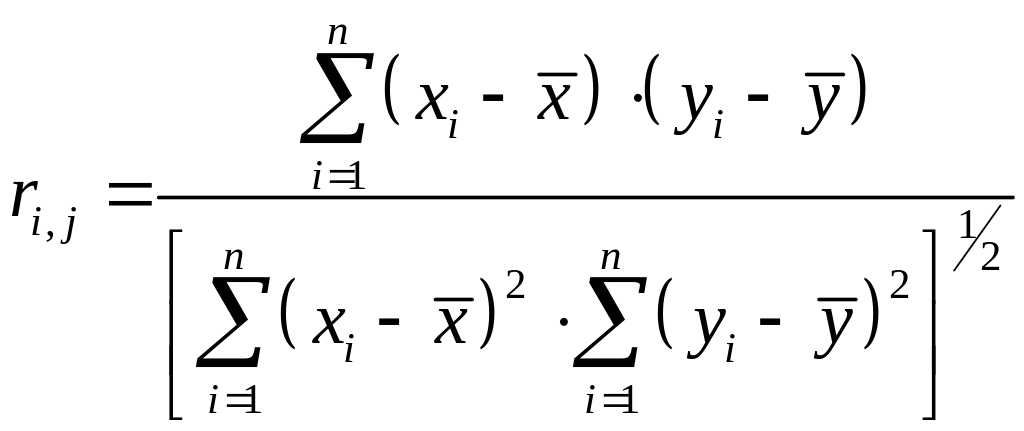 .
.
Обработка результатов при совместных измерениях. Аппроксимация методом наименьших квадратов
Одним из наиболее
общих типов эксперимента является
измерение нескольких значений двух
различных величин для исследования
функциональной связи между ними
(совместные измерения). Рассмотрим
вначале случай, когда величины связаны
линейной зависимостью вида
![]() .
Так как измерения проводятся с
погрешностью, возникает задача определение
прямой линии, которая наилучшим образом
аппроксимирует результаты измерений,
т.е. задача определения наилучших оценок
А
и В.
.
Так как измерения проводятся с
погрешностью, возникает задача определение
прямой линии, которая наилучшим образом
аппроксимирует результаты измерений,
т.е. задача определения наилучших оценок
А
и В.
Для упрощения будем полагать, что погрешность в измерении x пренебрежимо мала. Это допущение как правило не приводит к грубым ошибкам.
Считая, что
постоянные А
и В
известны для любого значения
можно вычислить точное значение
![]() :
:
![]() .
Считая, что
.
Считая, что
![]() подчиняется нормальному распределению:
подчиняется нормальному распределению:
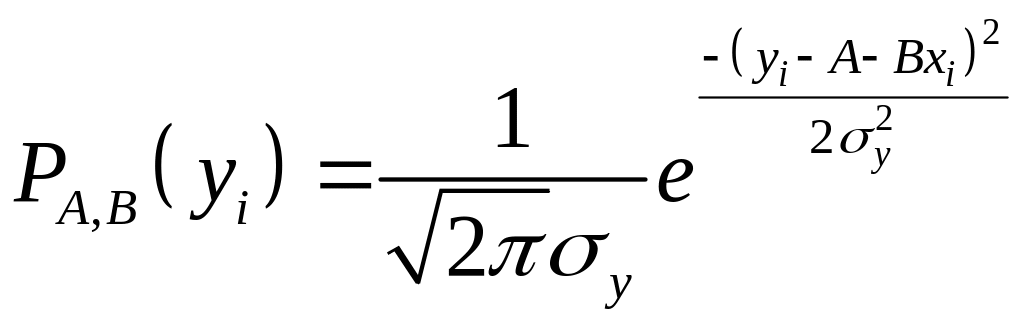 .
.
Вероятность
получения всего набора результатов
измерений
![]() равна произведению отдельных вероятностей
равна произведению отдельных вероятностей
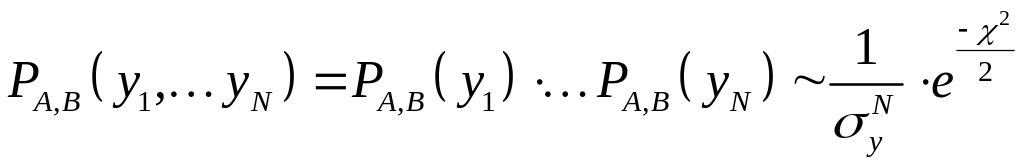 ,
,
где
 .
.
Наилучшей оценкой
для А
и В
являются их значения, для которых
![]() максимальна или соответственно минимальна
сумма
максимальна или соответственно минимальна
сумма
![]() .
Отсюда следует и название метода (метод
наименьших квадратов). Для нахождения
минимума продифференцируем
по А
и В
и приравняем производные нулю.
.
Отсюда следует и название метода (метод
наименьших квадратов). Для нахождения
минимума продифференцируем
по А
и В
и приравняем производные нулю.
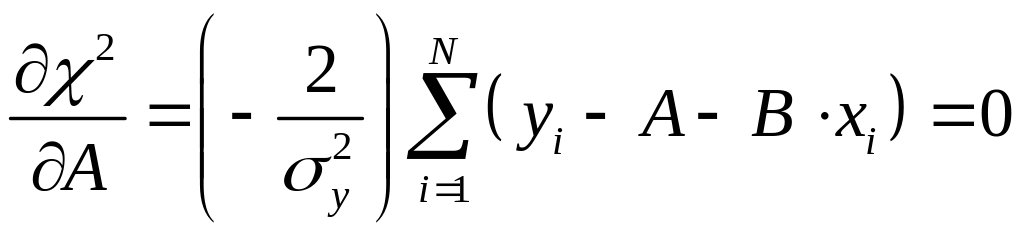 ;
;
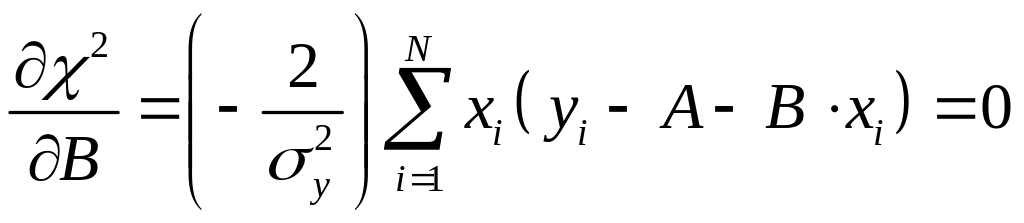 .
.
Эти выражения можно переписать в виде системы уравнений:
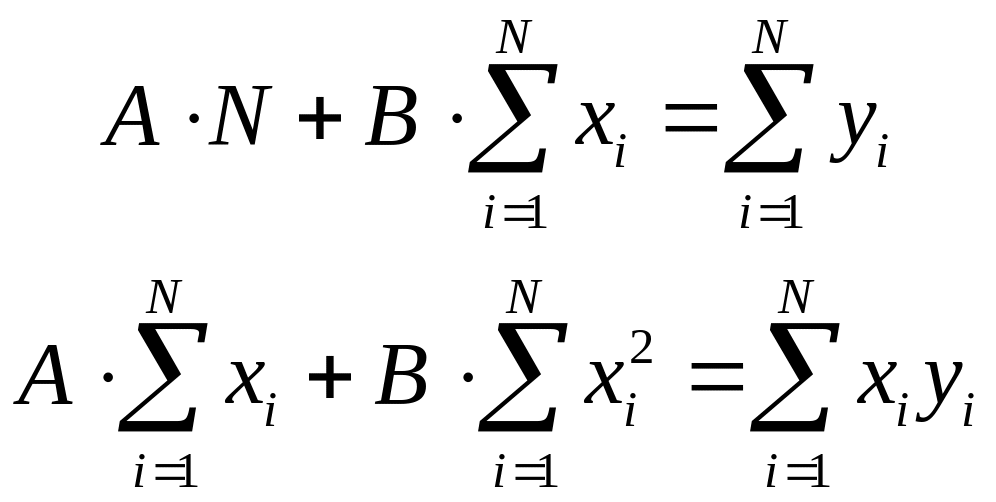 .
.
Решением этой системы можно записать в виде
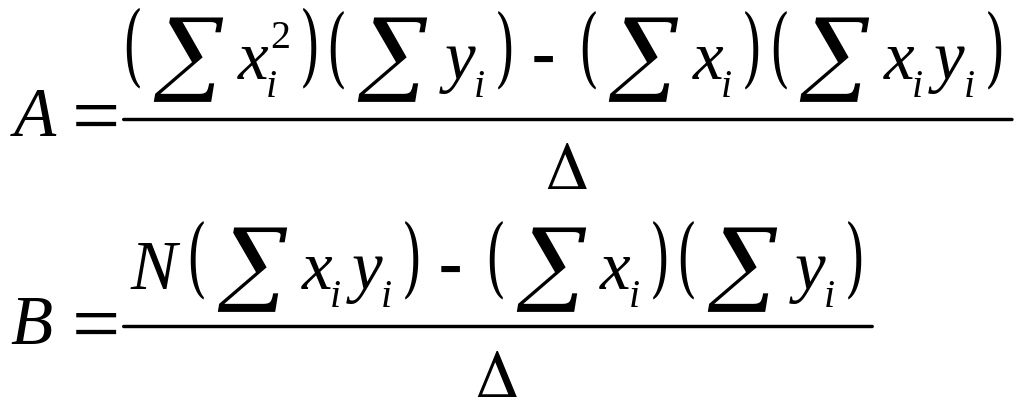 ;
;
![]() - детерминант
системы уравнений.
- детерминант
системы уравнений.
Полученная линия называется линией аппроксимации методом наименьших квадратов или линией линейной регрессии.
Аппроксимация другими зависимостями методом наименьших квадратов
Кроме рассмотренной линейной зависимости между двумя физическими величинами на практике встречается целый ряд других зависимостей. Например, часто одна переменная выражается через полином от второй переменной:
![]() ,
или представляется суммой тригонометрических
функций
,
или представляется суммой тригонометрических
функций
![]() .
Для всех возможных аппроксимационных
функций, линейных относительно параметров
А, В,
нормальные уравнения, определяющие
наилучшие оценки для А,
В, это система
линейных уравнений, которая может быть
получена рассмотренным выше способом.
.
Для всех возможных аппроксимационных
функций, линейных относительно параметров
А, В,
нормальные уравнения, определяющие
наилучшие оценки для А,
В, это система
линейных уравнений, которая может быть
получена рассмотренным выше способом.
Ряд физических величин связан между собой экспоненциальной зависимостью вида:
![]() .
.
Прямое применение изложенных выше методов приводит к таким уравнениям для А и В, которые не имеют простого решения. В этом случае целесообразно линеаризовать аппроксимационную функцию:
![]() .
.
При этом
![]() линейно связан с В,
и можно найти наилучшие оценки для
линейно связан с В,
и можно найти наилучшие оценки для
![]() и В.
и В.
![]() и
B
связаны линейно и к ним применим
расмотренный метод.
и
B
связаны линейно и к ним применим
расмотренный метод.
Объединение результатов разных измерений
Часто одна физическая величина измеряется несколько раз и возможно в разных местах. Предположим, что мы имеем два результата измерений, ошибки которых распределены по нормальному закону:
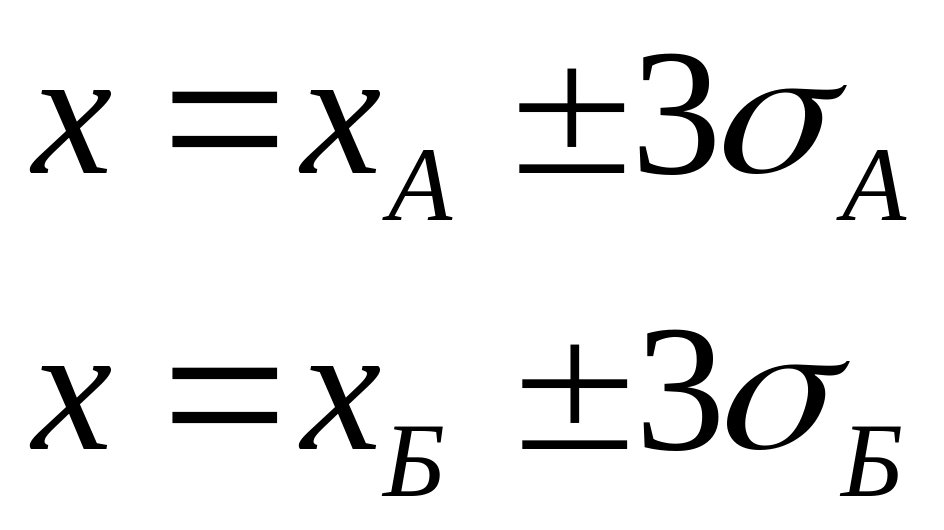 .
.
Каждый из результатов
может быть может быть получен в результате
обработки нескольких измерений. Прежде
всего необходимо обратить внимание на
то, что если модуль разности
![]() больше доверительных интервалов, то
эти измерения противоречивы и необходимо
тщательно проанализировать оба измерения,
чтобы проверить нет ли неисключенных
систематических погрешностей.
больше доверительных интервалов, то
эти измерения противоречивы и необходимо
тщательно проанализировать оба измерения,
чтобы проверить нет ли неисключенных
систематических погрешностей.
Если
меньше доверительного интервала, то
возникает проблема определения наилучшей
оценки истинного значения
![]() .
Вероятность получения частного результата
в рассматриваемых измерениях определяется
из следующих соотношений:
.
Вероятность получения частного результата
в рассматриваемых измерениях определяется
из следующих соотношений:
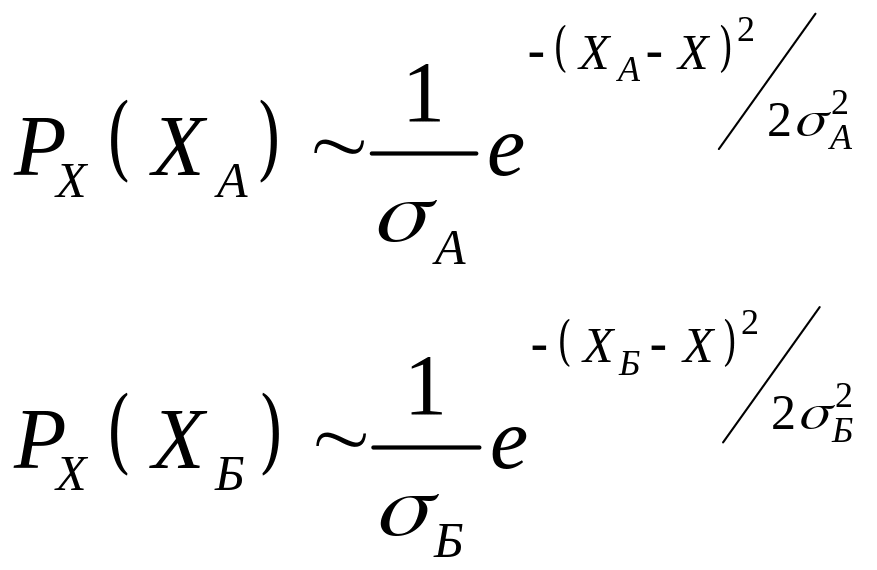
Совместная
вероятность
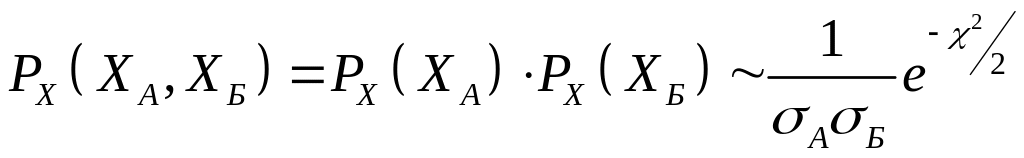 ,
,
где
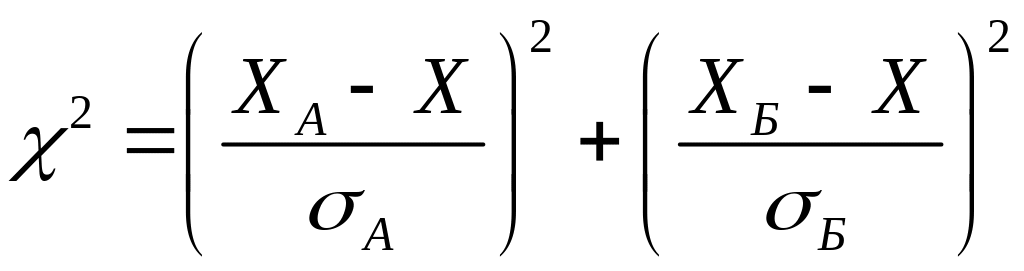 .
.
Наилучшей оценкой
для
в соответствии с методом максимального
правдоподобия будет значение, для
которого совместное получение величин
![]() и
и
![]() будет наиболее вероятным. Для этого
должно быть минимальным, т.е. должно
выполняться условие
будет наиболее вероятным. Для этого
должно быть минимальным, т.е. должно
выполняться условие
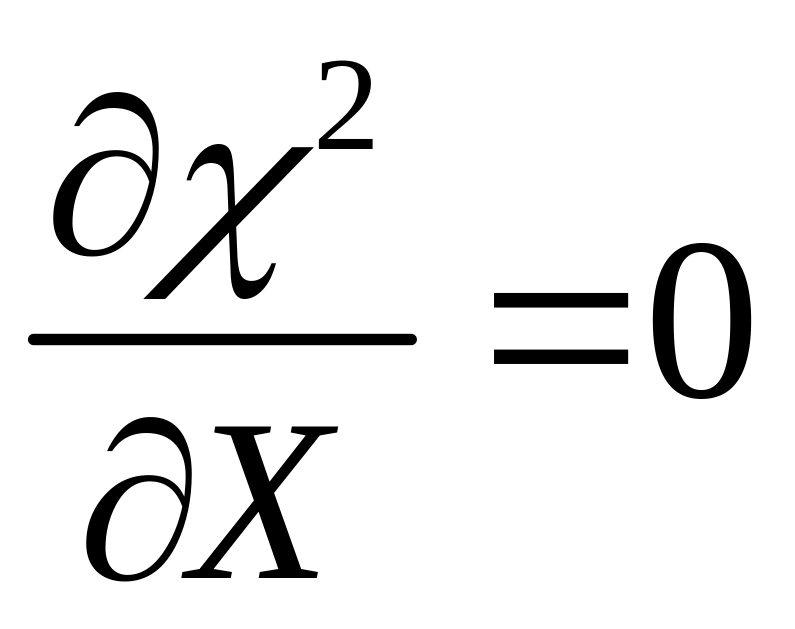 ,
которое можно записать в виде
,
которое можно записать в виде
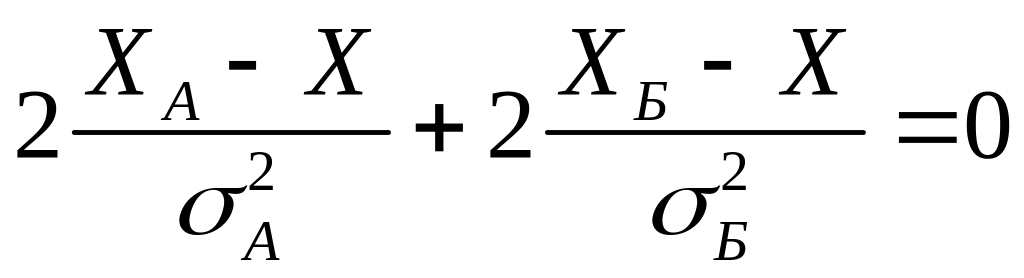 ,
,
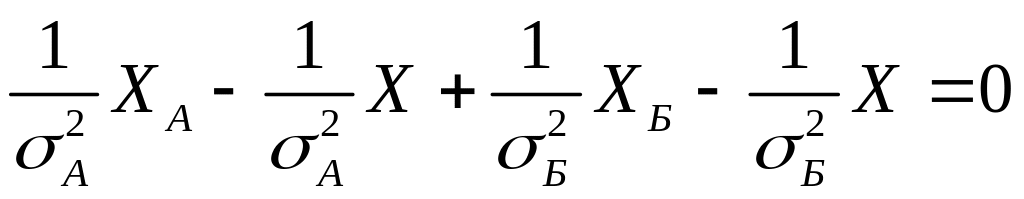 ,
,
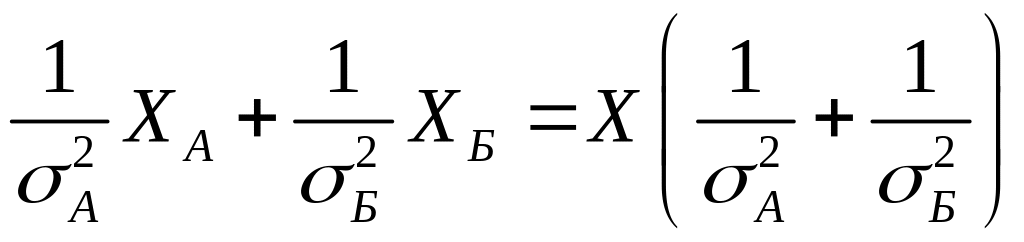 .
.
Решение уравнения относительно есть наилучшая оценка результата:
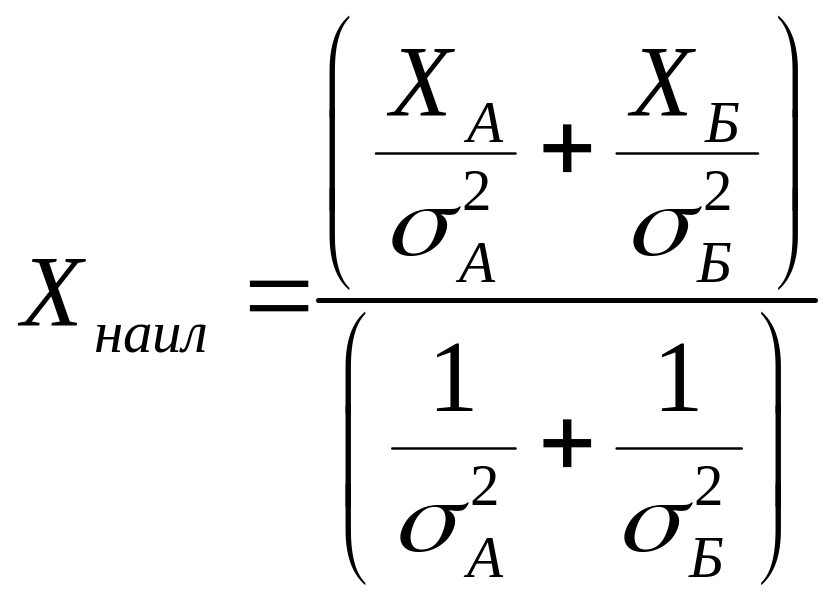 ,
или
,
или
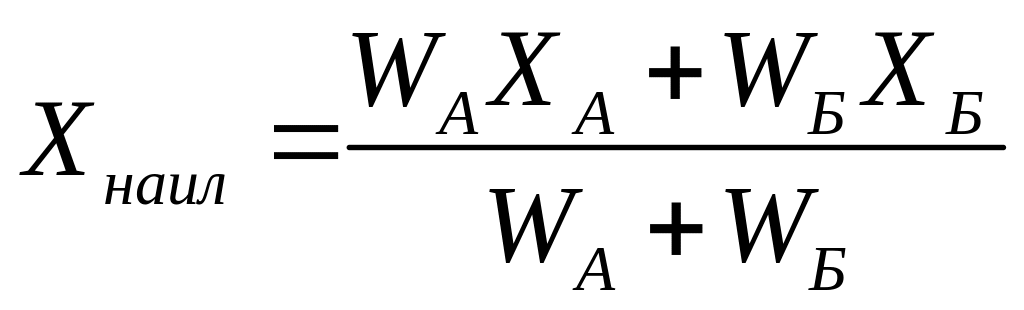 ,
где
,
где
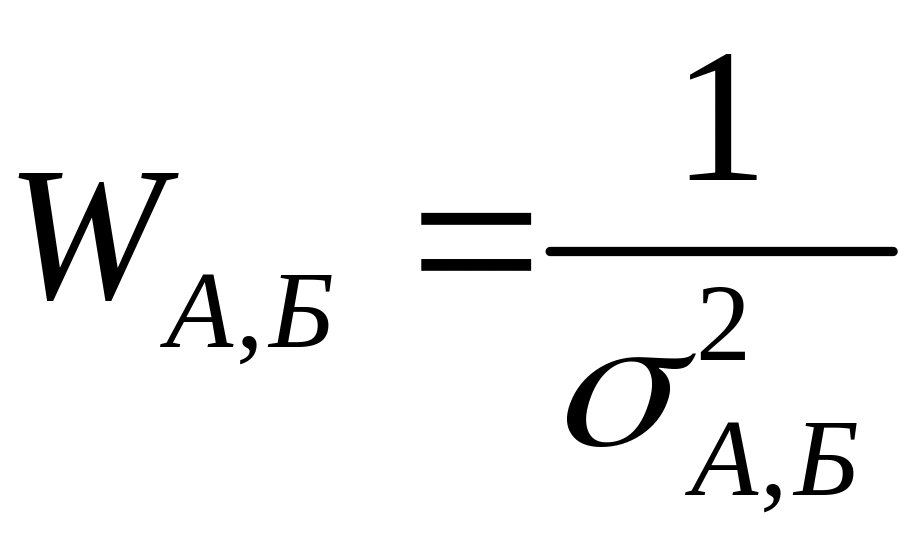 - вес соответствующего измерения.
- вес соответствующего измерения.
Полученная оценка
называется взвешенной средней оценкой.
Обобщая результат на
![]() измерений можно получить:
измерений можно получить:
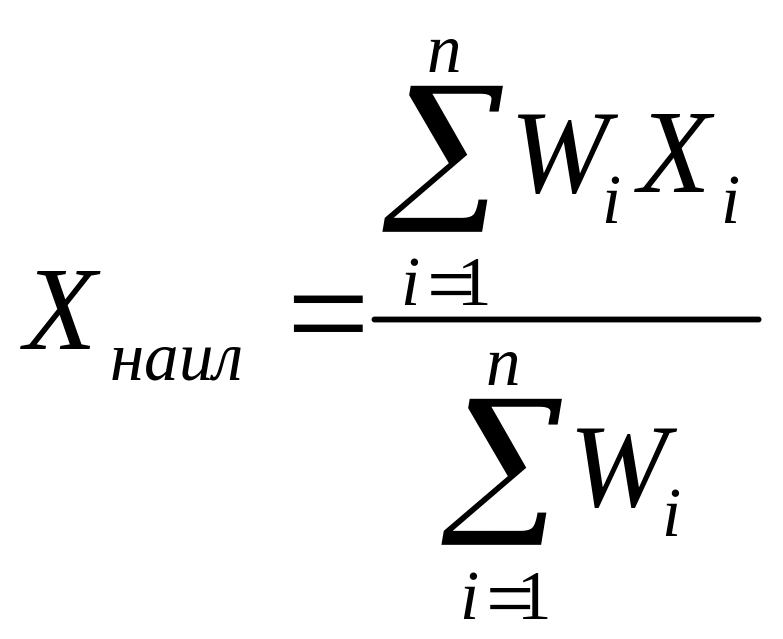
Как следует из выражения, любое менее точное измерение (с большей среднеквадратической погрешностью) вносит меньший вклад в конечный результат.