9. Вибір методу розв’язання мат. Задачі. Аналітичні та числові методи

Будь - яка задача , насамперед, представляється своїм фізичним змістом. За змістом задачі ми цілком розуміємо, що дано і що потрібно отримати,однак відповісти на поставлене запитання не можемо. Потрібно побудувати математичну модель, що адекватно відображає всі характеристики і взаємозв’язки в полі досліджуваної області. Математична модель являє собою сукупність формул, використовуючи які, можна одержати розв'язок задачі. Якщо отримані рівняння неможливо вирішити аналітично, або дуже складно, слід визначити до якого класу задач відноситься отримана мат модель (наприклад трансцендентне р-ня, система р-нь, диф р-ня, обчислення інтегралу, задача лінійного нелінійного програмування і т.д. ) і відповідно до цього визначити чисельний метод розв’язання . Для кожного класу задач існує достатня к-сть різних методів розв’язання. Вибір методу залежить від виду отриманих співвідношень, точності, з якою потрібно отримати розв'язок, к-сті ітерацій і т.д.

Коли метод визначений, його представляють у вигляді алгоритму. Готовий алгоритм програмують, компілюють, та перевіряють на відповідність фізичному змісту задачі.

Переваги та недоліки аналітичних методів:

+ можливість отримати розв'язок у вигляді формули, формулу можна досліджувати, вивчати, аналізувати;

+ дозволяють робити розрахунки конкретних числових значень;

+ допускають перевірку іншими дослідниками;

+ не потребують використання комп’ютерної техніки;

-Мають низький рівень універсальності (коло задач, що можна розв’язувати аналіт. методами дуже вузьке);

-Громісткість викладу формул.

Переваги та недоліки числових методів:

+ високий рівень універсальності;

+ мало чутливі до форми області і т.д.;

+ використовуються для нелінійних задач;

+ мають властивість гнучкості, що істотно підвищує можливість розв’язання;

+ можливість поєднання методу з обробкою результатів;

- Обґрунтування проблеми точності отримання числових результатів;

- Один набір результатів для одного вводу даних.

10. Точні та наближені методи. Оцінка похибки наближеного розв’язку

Точні – це методи, які принципово дозволяють отримати точний розв’язок за скінчену кількість дій (кроків).

Наближені – ітерація, наближення до розв’язку (границі послідовності). Обмежуються певною скінченою наближеністю (відсікає нескінчену послідовність).

Між наближеними та точними методами, також є аналітичні та числові.

Існують різні методи знаходження наближеного розв’язку, тобто способи побудови послідовності ітерацій {x_n}, однак всі вони мають спільні етапи: задати початкове наближення, знайти наближення, перевірити умову виходу з ітераційного процесу.

Найбільш часто використовується наступний критерій зупинки ітераційного процесу: |x_n+1–x_n|<ε, тобто різниця між сусідніми ітераціями становиться малою. Також для завершення ітераційного процесу використовується умова |f(x_n)|<ε , де f(x_n) – нев’язка методу.

Існують різні способи дослідження функції: аналітичний, табличний, графічний.

Похибка вимірювання — це відхилення результату вимірювання від істинного значення вимірюваної фізичної величини:

де - результат вимірювання величини ; - її істинне значення.

Похибка вимірювання є кількісною характеристикою точності вимірювання.

Розрізняють апріорні (теоретичні) та апостеріорні (практичної збіжності) оцінки похибки.

Апріорні оцінки виконуються ще до початку розв’язку задачі і використовуються саме формування задачі та алгоритм методу.

Для нескінченного ряду: , при , - точне,

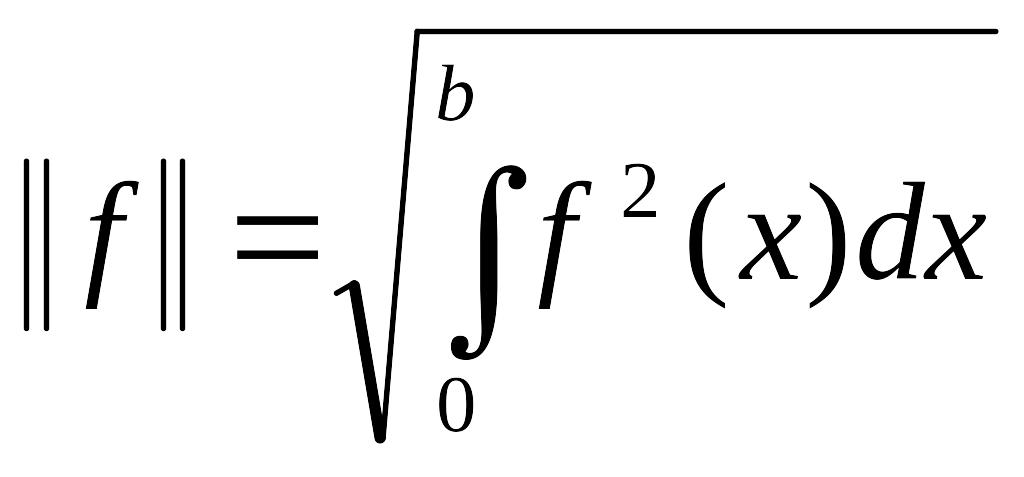
 При цьому не обов’язково знати точний розв’язок

 

n –const

Число a характеризує швидкість збіжності. Це число відіграє істотну роль в оцінці ефективності алгоритму. На відміну від a, стала с не має в таких оцінках якогось конкретного значення, с – невідома. З одного боку така оцінка корисна (показує швидкість спадання похибки при n кількості ітерацій). З іншого  - нічого не дає для конкретної характеристики похибки.

Апостеріорні оцінки здійснюються на основі аналізу отриманих результатів. Розглянемо деякі проблеми апостеріорних оцінок:

Порівняння з віддаленими «точними» розв’язками .

Порівняння отриманих наближених розв’язків з наближеними розв’язками, отриманих іншими методами та авторами.

Оцінка результатів у критичних ситуаціях.

Оцінка практичної збіжності важлива характеристика, яку ми можемо отримати при реакції задач

a₁, a₂…a_n

  Якщо після певної кількості ітерацій значення параметру a практично не змінюється, то кажуть, що процес практично збігається. Визначається потрібна кількість ітерацій *.