1.1.3. Закони ідеальних газів

Характеристики ідеального газу:

1. концентрація молекул приблизно ;

2. середня відстань між молекулами ;

3. сумарний власний об’єм молекули, що знаходяться в газу складає (даним об’ємом можна знехтувати).

На основі експериментів з такими газами було встановлено ряд закономірностей, які виконувались для ідеальних газів обов’язково, а для реальних газів можуть бути виконані лише при певних умовах (не дуже високих температурах і відносно низькому тиску, простій структурі, малих розмірах і низькій концентрації).

Закон Бойля-Маріотта (1662р.).

При постійній температурі об’єм даної маси газу обернено пропорційний його тиску:

, (1)

c – постійна величина, пропорційна кількості молів газу і його абсолютній температурі.

Закон Гей-Люссака (1802р.).

Об’єм даної маси газу при постійному тиску змінюється лінійно з температурою:

, (2)

, - об’єми газу при температурі T і 0 ;

- термічний коефіцієнт розширення при постійному тиску.

Для всіх газів при нормальних умовах:

. (3)

За абсолютною шкалою температур:

. (4)

Закон Шарля (1787р.).

Тиск даної маси газу при постійному об’ємі змінюється лінійно з температурою:

, (5)

- тиски газу при температурі Т і 0 ;

- термічний коефіцієнт тиску при постійному об’ємі.

Для всіх газів при нормальних умовах .

За абсолютною шкалою температур:

. (6)

Закон Авогадро.

Гей-Люссак сформулював закон з’єднаних об’ємів для газів: об’єм газів, що реагують або що утворюються у результаті хімічних реакцій, знаходяться у відношеннях невеликих цілих чисел. Авогадро висунув гіпотезу, що в рівних об’ємах різних газів при однаковій температурі і тиску знаходиться однакове число молекул.

Один моль будь-якого газу, який є подібним до ідеального газу при однаковій температурі і тиску, займає однаковий об’єм.

При нормальних умовах даний об’єм:

.

1.1.4. Рівняння стану ідеального газу

Об’єм даної маси газу є функцією від p і T:

,

тоді повний диференціал визначається як похідна:

. (7)

Рівняння (4) запишемо у вигляді:

,

тоді з рівнянь (1) і (.4):

(8)

Якщо підставити рівняння (8) у рівняння (7), то отримаємо:

. (9)

Якщо проінтегрувати, то:

. (10)

Потенціюючи дане рівняння, отримаємо:

. (11)

Дане рівняння було отримане французьким фізиком Клайпероном у1834році. У 1884 році Менделєєв придав рівнянню (11) універсального вигляду, записавши його для 1 моль газу з об’ємом V:

, (12)

- постійна величина, універсальна газова стала:

.

Якщо помножити (12) на кількість молів , отримаємо рівняння стану ідеального газу для довільної маси:

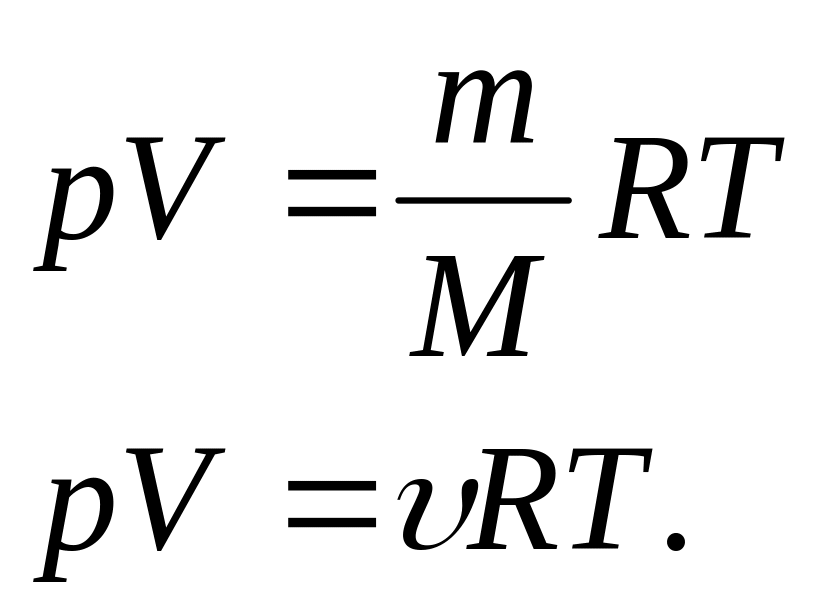(13)

Останнє рівняння – рівняння Менделєєва-Клайперона.

1.1.5. Основне рівняння мкт газів

(тиск газу з точки зору МКТ)

Для ідеального газу розмірами молекул та зіткненнями між ними можна знехтувати. Потрібно враховувати зіткнення молекул зі стінками посудини.

Нехай газ знаходиться в посудині , що має форму прямокутного паралелепіпеда, стінки якого ідеально-відображаючі:

Рис. 3

Розрахуємо тиск газу на стінку з площею S. При зіткненні молекули газу зі стінкою посудини, зміниться складова, що перпендикулярна до грані. Відповідна зміна імпульсу молекули при одиничному зіткненні її зі стінками:

.

За одиницю часу молекула здійснює z таких ударів:

,

- середній час ,за який молекула здійснює 1 удар:

,

тоді:

.

Відповідно з 2 і 3 законами Ньютона, результуюча сила, що діє на стінку зі сторони N молекул газу, що знаходяться в посудині дорівнює половині зміни імпульсу:

. (14)

Тиск газу на грань, яка розглядається, визначається як відношення сили, що діє на грань на площу S грані:

, (15)

V – об’єм, який займає даний газ.

Значення дії тиску на інші грані:

(16)

Так як в стані термодинамічної рівноваги газу рух молекул у всіх напрямках буде рівномірним, то:

Згідно з теоремою Піфагора:

,

тоді можна записати:

.

Для кожної з цих складових:

,

тому тиск газу на стінки посудини визначається за формулою:

, (17)

- кінетична енергія усіх молекул газу.

Для однорідного газу маса усіх молекул однакова, а швидкості – різні, тому рівняння для тиску:

, (18)

n - концентрація молекул в одиниці об’єму.

Рівняння (17) і (18) використовуються в релятивістському і нерелятивістському русі, але в релятивістському русі необхідно враховувати залежність маси від швидкості руху.