Многоканальная смо с неограниченной очередью

Снимем ограничение на длину очереди в задаче предыдущего раздела.

Вероятности состояний получим предельным переходом (при ); это возможно при x<1, т.е. при .

Получим выражения предельных вероятностей состояний:

Для такой системы в формулах (3.25)  (3.27) устремим , получим

Определение показателей смо

П р и м е р 1. Имеем одну телефонную линию. Заявка-вызов, пришедшая в момент, когда линия занята, получает отказ. Интенсивность потока вызовов   = 0,8 вызовов в минуту, средняя продолжительность разговора  t_обсл = 1,5 мин. Найти вероятности состояний, абсолютную пропускную способность А, относительную пропускную способность q и вероятность отказа  _отк.

Р е ш е н и е. Интенсивность обслуживания для одноканальной СМО с отказами  = 1/t_обс=1/1,5 = 0,667.

Вероятность состояний согласно формулам (3.11) и (3.12)

q = 0,455  45%; p _отк= 0,545; А = 0,8  0,455= 0,364.

Итак, относительная пропускная способность линии 45% вызовов, 55% вызовов получают отказ, абсолютная пропускная способность 0,364 разговоров в минуту.

П р и м е р 2. Пусть телефонных линий будет три (n=3);  = 0,8;  = 0,667. Найти вероятность состояний, абсолютную и относительную пропускную способность, вероятность отказа и среднее число занятых каналов.

Указание. Среднее количество занятых каналов вычислить двумя способами:

• с помощью готовых формул (3.15  3.16);

• вычислением математического ожидания случайной величины – числа занятых каналов, используя вероятности состояния системы.

Р е ш е н и е. Состояния системы следующие (рис. 3.4):

S₀  все линии свободны;

S₁  занята одна линия;

S₂  занято две линии;

S₃  занято три линии.

Вероятности состояний и характеристики многоканальной СМО с отказами вычислим по формулам (3.11  3.16):

р₁ = 0,374; р₂ = 0,224; р₃  = 0,090; р_отк = р₃ = 0,090;

q = 0,910; A = 0,728; k = 1,2  0,910 = 1,09.

Вычисление среднего числа занятых каналов приведено на рис.3.7-3.8. Ячейка С20 содержит искомое значение, которое совпало со значением, вычисленным по формуле (3.16).

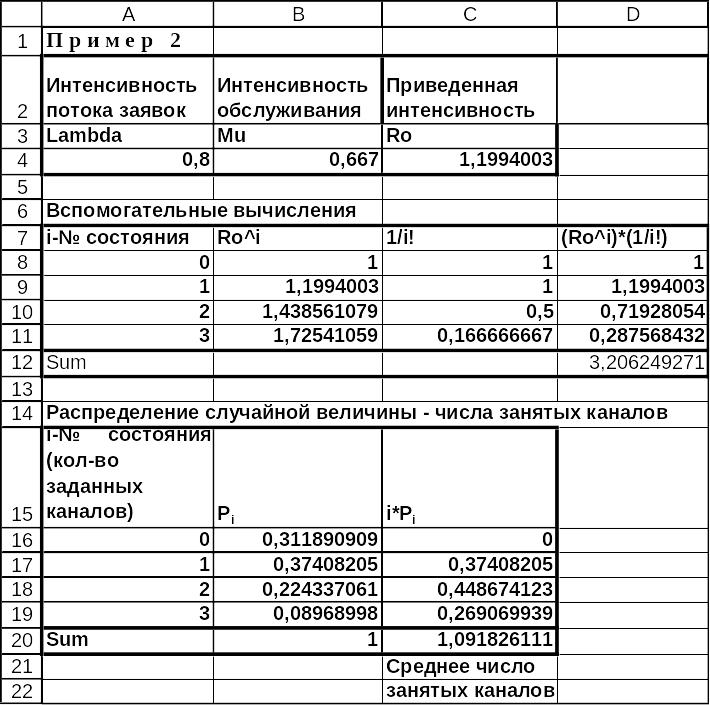
Рис.3.7 Решение примера 2 в MS Excel в режиме отображения данных.

Рис.3.8 Решение примера 2 в MS Excel в режиме отображения формул.

П р и м е р 3. СМО представляет собой экскаватор, работающий на уступе в карьере. К нему на погрузку идет поток автосамосвалов с интенсивностью  = 1 машина в минуту. Процесс погрузки продолжается в среднем 1,25 мин. Площадка на уступе ограничивает количество машин в очереди до трех. Определить вероятность отказа р_отк ; относительную (q) и абсолютную (А) пропускную способности; среднее число машин, ожидающих погрузки ; среднее число машин, находящихся на уступе ; среднее время ожидания в очереди ; среднее время пребывания в системе .

Указание. Средние количества машин стоящих в очереди, находящихся на обслуживании и находящихся в системе вычислить двумя способами:

• с помощью готовых формул (3.19  3.20);

• вычислением математических ожиданий соответствующих случайных величин – количества машин стоящих в очереди, находящихся на обслуживании и находящихся в системе, используя вероятности состояния системы.

Р е ш е н и е. Состояния системы (рис.3.5) следующие:

S₀  экскаватор свободен, очереди нет;

S₁  экскаватор занят, очереди нет;

S₂  в очереди один автосамосвал;

S₃  в очереди два автосамосвала;

S₄  в очереди три автосамосвала.

Вероятности состояний:

(k =1, 2, 3, 4), где .

Характеристики системы вычислим по формулам (3.173.21).

Так как  = 1/1,25 = 0,8 , соответственно  =1/0,8=1,25, то

p₀ = 0,122; p₄  =  0,297; р_отк = p₄  = 0,297;

q = 0,703; A = 0,703;

 = 1,56; = 2,44;  = 1,56 мин; =  2,44.

Вычисление средних количеств машин, стоящих в очереди, находящихся на обслуживании и находящихся в системе, приведено на рис.3.9-3.10. Ячейка С23 содержит искомое значение среднего количества машин стоящих в очереди. Ячейка С37 содержит искомое среднее количество загружаемых машин. Ячейка С50 содержит искомое значение - среднее количество машин, находящихся на обслуживании. Все эти значения совпали со значениями, вычисленными по формулам (3.173.21).

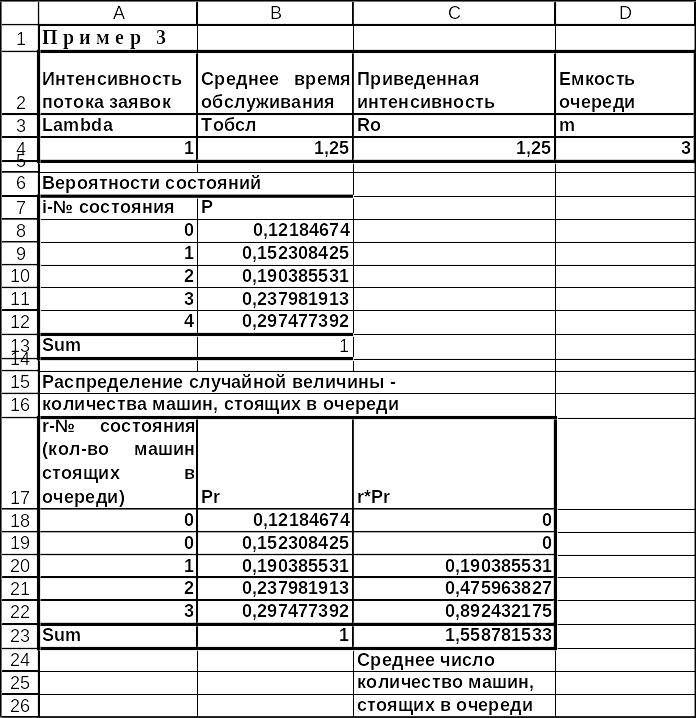
Рис.3.9 Решение примера 3 в MS Excel в режиме отображения данных(начало).

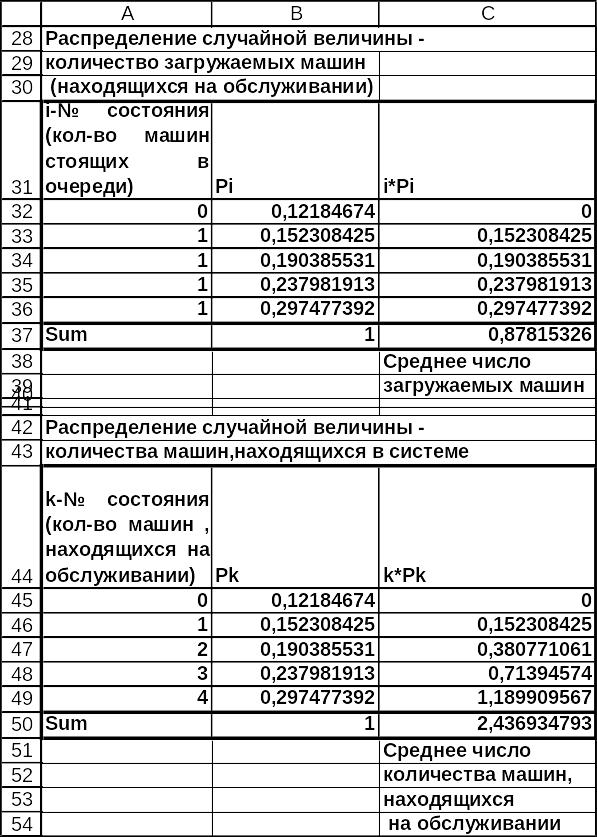
Рис.3.10 Решение примера 3 в MS Excel в режиме отображения данных(окончание).

Рис.3.11 Решение примера 3 в MS Excel в режиме отображения формул.

П р и м е р 4. На обогатительную фабрику прибывают составы с рудой с интенсивностью  = 2 состава в час. Среднее время обработки состава t_обсл = 0,4 ч. Очередь на разгрузку предполагается неограниченной. Найти среднюю длину очереди, среднее число составов в системе, среднее время ожидания и среднее время пребывания в системе.

Р е ш е н и е. Так как = 2 0,4 = 0,8 , т.е. < 1, то вероятности состояний и характеристики системы можно получить из формул (3.13  3.15). Таким образом,  = 3,2 состава;  = 1,6 час; = 2 ч.

П р и м е р 5. На уступе в карьере работает два экскаватора с одинаковой производительностью (n = 2). Поток автосамосвалов, прибывающих на уступ для погрузки, имеет интенсивность  = 2 машины в минуту; среднее время погрузки t_обсл = 2 мин. Площадка на уступе может вместить очередь не более трех машин (m = 3). Найти вероятность отказа, относительную и абсолютную пропускную способность, среднее число занятых экскаваторов и машин в очереди, среднее время ожидания и пребывания машин на уступе.

Р е ш е н и е. Состояния в системе следующие (рис. 3.4):

S₀  система свободна;

S₁  занят погрузкой один экскаватор;

S₂  оба экскаватора заняты, очереди нет;

S₃  оба экскаватора заняты, в очереди одна машина;.

S₄  в очереди два автосамосвала;

S₅  в очереди три автосамосвала.

Вероятности состояний и характеристики многоканальной СМО с ожиданием вычислим по формулам (3.16  3.20).

Итак, n = 2, m = 3;  = 2;  = 0,5; = 4; x =  / n = 2.

Соответственно:

p₀ = 0,008; р_отк = 0,512; q = 0,488; A = 0,976;

 = 2,18; = 1,952;  = 1,09 мин; =  2,07.