СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ

Методические указания к лабораторным работам

для студентов специальностей 080502, 080507

САНКТ-ПЕТЕРБУРГ

2010

Министерство образования и науки РФ

Государственное образовательное учреждение высшего профессионального образования

Санкт-Петербургский государственный горный институт им Г.В. Плеханова

(технический университет)

Кафедра информатики и компьютерных технологий

СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ

Методические указания к лабораторным работам

для студентов специальностей 080502, 080507

САНКТ-ПЕТЕРБУРГ

2010

УДК 519.86:622.3.012 (075.83)

МЕТОДЫ И МОДЕЛИ В ЭКОНОМИКЕ. Системы массового обслуживания.

Методические указания для выполнения лабораторных работ./ Санкт-Петербургский горный ин-т. Сост.: В.В Беляев, Г.Н. Журов, Т.Р Косовцева. СПб, 2010 . 58 с.

Методические указания содержат необходимые теоретические сведения и примеры решения типовых задач по определению показателей системы массового обслуживания (СМО), а так же решение конкретной экономической задачи по определению оптимальных параметров.

Предназначены для студентов экономических специальностей

Табл. 10. Рис.32. Библиогр.: 2 назв.

Научный редактор доц. Г.А. Прудинский

© Санкт-Петербургский горный

институт им. Г.В.Плеханова, 2010 г.

Введение

Стохастическая модель — такая экономико-математическая модель, в которой параметры, условия функционирования и характеристики состояния моделируемого объекта представлены случайными величинами и связаны стохастическими (т. е. случайными, нерегулярными) зависимостями, либо исходная информация представлена случайными величинами. Следовательно, характеристики состояния в модели определяются не однозначно, а через законы распределения их вероятностей. При построении стохастических моделей могут применяться методы корреляционного и регрессионного анализов, другие статистические методы. Рассмотрим моделирование стохастических процессов на примере систем массового обслуживания.

С системами массового обслуживания (СМО) часто приходится иметь дело на практике, поэтому умение исследовать такие системы является важной частью образования экономиста. При некоторых упрощающих предположениях СМО могут исследоваться аналитическими методами. Это позволяет на примерах таких систем изучить характерные особенности более сложных СМО. Решение конкретных задач по определению показателей СМО способствует развитию важного для специалиста умения работать со случайными величинами и позволяет увидеть преимущества вероятностных методов по сравнению с детерминированными, традиционно используемыми экономистами при определении характеристик СМО.

Лабораторные работы № 3-4. Моделирование простейшего потока событий. Определение показателей смо

Цель: освоить решение задачи по определению показателей и оптимальных параметров СМО.

Получить представление о следующих понятиях:

• простейший поток событий;

• закон распределения Пуассона, экспоненциальный закон распределения и их характеристики;

• имитационное моделирование производственных процессов. Основные понятия имитационного моделирования;

• структура СМО;

• классификация СМО по различным признакам;

• показатели функционирования СМО.

Теоретические сведения. Базовые понятия

Системами массового обслуживания (СМО) называют системы, функционирование которых заключается в обслуживании большого количества заявок. Примеры систем массового обслуживания приведены в табл.3.1.

Таблица 3.1

Примеры систем массового обслуживания

СМО	Заявки	Каналы
Автобусный маршрут и перевозка пассажиров	Пассажиры	Автобусы
Производственный конвейер по обработке деталей	Детали, узлы	Станки, склады
Автосамосвалы и экскаваторы при проведении открытых горных работ	Автосамосвалы	Экскаваторы
Чиновники, ведущие прием граждан	Граждане	Чиновники
Задачи, решаемые процессором компьютера	Задачи	Процессор компьютера

В составе СМО можно выделить следующие основные части (рис.3.1):

1. Входящий поток заявок;

2. Накопитель -  место, где заявки могут ждать освобождения обслуживающих устройств, и формируется очередь на обслуживание;

3. Узел обслуживания - система приборов, обслуживающих заявки (устройства, каналы);

4. Выходящий поток заявок, т.е. заявок, которые обслужены, или тех, которым в обслуживании было отказано.

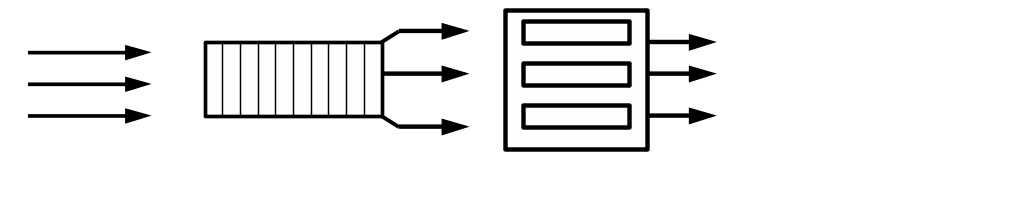
Рис. 3.1. Принципиальная схема системы массового обслуживания.

Система с накопителем называется СМО с ожиданием, без накопителя  СМО с отказами.

В зависимости от емкости накопителя различают СМО с конечной и бесконечной очередью.

Все системы массового обслуживания классифицируются по правилам их работы следующим образом:

1. Системы с отказами, в которых заявка, поступившая в момент, когда все каналы заняты, покидает СМО;

2. Системы с очередью (с ожиданием), в которых заявка, поступившая в момент, когда все каналы заняты, становится в очередь до освобождения одного из каналов; системы с очередью делятся на системы с ограниченным и системы с неограниченным ожиданием.

Порядок, в котором формируется очередь на обслуживание, называется дисциплиной очереди. Различают следующие дисциплины обслуживания: бесприоритетные и приоритетные.

Важнейшие бесприоритетные дисциплины обслуживания:

• FIFO (First In, First Out — первым пришел, первым ушел): если заявка первой пришла в очередь, то она первой уйдет на обслуживание;

• LIFO (Last In, First Out — последним пришел, первым ушел): если заявка последней пришла в очередь, то она первой уйдет на обслуживание (пример — патроны в рожке автомата);

• SF (Short Forward — короткие вперед): в первую очередь обслуживаются те заявки из очереди, которые имеют меньшее время обслуживания.

• RANDOM (случайный выбор).

При приоритетном обслуживании заявке задается некоторый параметр, который определяет его приоритет. Этот параметр может задаваться в числовом виде (статический приоритет) или в виде функции, которая зависит от времени пребывания в системе (динамический приоритет).

В системах с ожиданием накопитель в общем случае может иметь сложную структуру.

Если источник входящего потока заявок расположен вне системы, то СМО называется открытой, а если обслуженная заявка через некоторое время снова возвращается во входящий поток, то СМО называется замкнутой.

Основные показатели функционирования СМО могут быть вычислены в зависимости от типа СМО

Поскольку заявки поступают на обслуживание в СМО в случайные моменты времени, имеет смысл говорить о потоке заявок, характеристикой которого служит закон распределения. Обслуживание поступившей заявки продолжается некоторое (тоже случайное) время, что приводит к тому, что в какие-то промежутки времени поступившие заявки либо образуют очередь на обслуживание, либо покидают систему необслуженными, в другие же периоды СМО может работать с недогрузкой.

Анализ зависимости между характером потока заявок, числом каналов, их производительностью и эффективностью обслуживания и есть предмет теории систем массового обслуживания (СМО). Одним из основных математических понятий в теории СМО является понятие потока событий.

Поток событий — это последовательность однородных событий, наступающих одно за другим в случайные промежутки времени. На оси времени эти события могут быть изображены, как показано на рис.3.2. ,

где τ_j — интервал между событиями (случайная величина);

t_сi — момент совершения i-го события (отсчитывается от t = 0);

T_н — время наблюдения.

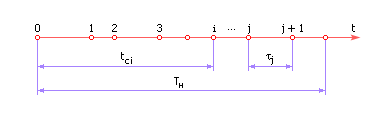
Рис. 3.2. Пример потока событий

Простейший поток определяется тремя условиями:

1. Стационарностью – среднее число требований в единицу времени постоянно;

2. Отсутствием последействия – число требований, поступающих в некоторый промежуток времени, не зависит от числа требований, поступивших в предыдущем промежутке;

3. Ординарностью – вероятность поступления более одного требования в малый промежуток времени есть малая величина более высокого порядка, чем , т.е. в очень малый промежуток времени поступает не более одного требования.

Типичный пример такого потока событий приведен на рис.3.3. На оси времени маркерами отмечены моменты времени, когда наступают события. Заметим, что визуально нельзя обнаружить закономерность появления событий, интервал времени между соседними событиями различен, а в единицу времени наступает различное количество событий. Так за 1-ую единицу времени наступает три события, за 6-ую - два события, за 7-ую -четыре события. Т.е. количество событий, наступающих в единицу времени является случайной величиной. Однако, если сосчитать N - количество событий наступивших за достаточно длинный интервал времени T_н (например, за 1 час, T_н =60 мин.) и вычислить среднее количество событий в минуту N /T_н., то это среднее количество будет приблизительно одинаковым, независимо от того с какого момента времени отсчитывать интервал времени.

Рис. 3.3. Пример простейшего потока событий

Установлено, что интервал времени между событиями в этом потоке есть случайная величина, распределенная по показательному (по экспоненциальному) закону, плотность которого определяется формулой:

(3.1)

где - параметр распределения.

Как известно, математическое ожидание случайной величины M(X) распределенной по показательному закону; равно , а дисперсия D(X) равна 1/λ².

M(X)=1/λ; D(X)=1/λ²

Используя основное свойство математического ожидания случайной величины, приходим к выводу о том, что средний интервал времени между двумя событиями в потоке равен . Отсюда следует, что среднее число событий, происходящих в единицу времени, равно обратной величине т.е. . Т.о., характеризует интенсивность потока, и оно равно среднему количеству событий происходящим в единицу времени.

Для непрерывного распределения, зная плотность распределения f(x), можно найти функцию распределения F(x) по формуле

. (3.2)

Случайная величина, следующая экспоненциальному распределению, имеет функцию распределения

(3.3)

Знание функции плотности и функции распределения позволит вычислить - вероятность того, что промежуток времени между двумя событиями в потоке не меньше a и меньше b. Эта вероятность равна определенному интегралу от плотности, взятому в пределах от a до b,

(3.4)

Если и , то

(3.5)

Другой случайной величиной, связанной с простейшим потоком событий является количество событий, происходящих в единицу времени. Эта случайная величина распределена по закону Пуассона. Это распределение является дискретным распределением и описывается формулой

  (3.6)

где λ>0– параметр распределения.

Формула (3.6) позволяет вычислить вероятность того, что в течение одной минуты произойдет ровно k событий. Основные описательные статистики для распределения Пуассона, выражаются следующими соотношениями (3.7):

M(X)=λ;   D(X)=λ (3.7)

Поскольку математическое ожидание случайной величины M(X) распределенной по закону, равно, то среднее число событий в потоке происходящих в единицу времени, равно .

Необходимо отметить, что оба распределения (экспоненциальное и распределение Пуассона), описывающие один и тот же поток событий, содержат один и тот же параметр λ, характеризующий интенсивность потока.

Математический анализ работы СМО становится весьма простым, если случайный процесс, протекающий в системе, имеет специфический характер (является марковским). Таким он будет, если все потоки событий (поток заявок, поток обслуживания и т.д.), переводящие систему из состояния в состояние, - простейшие.

Поэтому при моделировании СМО часто принимают допущение о том, что поток входящих заявок (требований) и поток обслуженных требований являются простейшими.

В данной работе будем полагать, что интенсивность потока входящих заявок равна , для описания этого потока справедливы формулы (3.1)- (3.7).

Поскольку поток обслуженных требований также является простейшим, то он имеет свою интенсивность равную . Для описания потока обслуженных требований также справедливы формулы (3.1)- (3.7) , с заменой на . Например, интервал времени между событиями в этом потоке (время обслуживания одного требования) есть случайная величина, распределенная по показательному закону:

(3.8)

где  - интенсивность обслуживания. При этом среднее время обслуживания одного требования равно

(3.9)

При анализе СМО часто используется характеристика, которая называется приведенной интенсивностью потока требований, равная отношению интенсивности потока входящих заявок к интенсивности обслуживания заявок. Обозначим это отношение через .

(3.10)

Приведенная интенсивность потока требований характеризует число требований, поступивших в систему за время обслуживания одного. Чтобы показать справедливость этого утверждения, приведем следующие соотношения:

Судить о результатах работы СМО можно по следующим показателям:

• относительная пропускная способность системы;

• абсолютная пропускная способность системы;

• вероятность отказа клиенту в обслуживании;

• вероятность занятости всех каналов;

• среднее количество занятых каналов;

• вероятность простоя каждого канала;

• вероятность простоя всей системы;

• среднее количество заявок, стоящих в очереди;

• среднее время ожидания заявки в очереди;

• среднее время обслуживания заявки;

• среднее время нахождения заявки в системе;

• среднее время занятости каждого канала;

• вероятность занятости каждого из каналов.

Судить о качестве полученной системы нужно по совокупности значений показателей. К числу важнейших показателей относятся: относительная и абсолютная пропускные способности системы. Абсолютная пропускная способность системы - это среднее количество требований, обслуживаемых в единицу времени. Относительная пропускная способность системы - это средняя доля обслуженных требований от общего числа поступивших, другими словами это вероятность обслуживания клиента системой.