МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Бронницкий филиал

«МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ)»

МАДИ

букерма л. б.

ФИЗИКА

Часть 4. Волны, термодинамика

Методические указания

по выполнению лабораторных работ по физике

для студентов, обучающихся по специальности

190601 «Автомобили и автомобильное хозяйство»

Бронницы 2011

Бронницкий филиал

«МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ)»

Кафедра МЕН

	«УТВЕРЖДАЮ» Заместитель директора Бронницкого филиала МАДИ (ГТУ) _ ___________________ С.Н.Пестова

букерма л. б.

ФИЗИКА

Часть 4. Волны, термодинамика

Методические указания

по выполнению лабораторных работ по физике

для студентов, обучающихся по специальности

190601 «Автомобили и автомобильное хозяйство»

Бронницы 2011

Перечень лабораторных работ

1. Нормальные моды струны.

2. Определение скорости звука.

3. Опыт Юнга.

4. Изучение дифракционной решетки.

5. Определение отношения теплоемкостей газа при постоянном давлении и постоянном объеме.

Лабораторная работа № 1.

Нормальные моды струны

Цель работы:

• Знакомство с компьютерной моделью колебания струны.

• Экспериментальное исследование процесса возникновения стоячих волн.

• Экспериментальное определение нормальных мод струны.

Основные понятия:

Если волны, бегущие по струне во встречных направлениях, имеют синусоидальную форму, то при определенных условиях они могут образовать стоячую волну.

Пусть струна длины l закреплена так, что один из ее концов находится в точке x = 0, а другой – в точке x = l. В струне создано натяжение T.

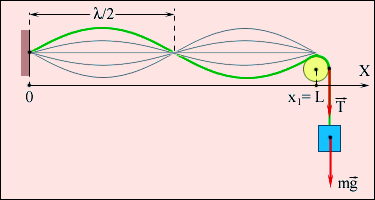
Рисунок 1 Стоячая волна

По струне одновременно распространяются в противоположных направлениях две волны одной и той же частоты:

y₁(x, t) = A cos (ωt + kx) – волна, бегущая справа налево;

y₂(x, t) = –A cos (ωt – kx) – волна, бегущая слева направо.

В точке x = 0 (один из закрепленных концов струны) падающая волна y₁ в результате отражения порождает волну y₂. При отражении от неподвижно закрепленного конца отраженная волна оказывается в противофазе с падающей. Согласно принципу суперпозиции

y = y₁ + y₂ = (–2A sin ωt) sin kx.

Это и есть стоячая волна. В стоячей волне существуют неподвижные точки, которые называются узлами. Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями.

Оба неподвижных конца струны должны быть узлами. Приведенная выше формула удовлетворяет этому условию на левом конце (x = 0). Для выполнения этого условия и на правом конце (x = l), необходимо чтобы kl = nπ, где n – любое целое число. Это означает, что стоячая волна в струне возникает не всегда, а только в том случае, если длина l струны равняется целому числу полуволн:

Набору значений λ_n длин волн соответствует набор возможных частот f_n:

где

скорость распространения поперечных волн по струне. Каждая из частот f_n и связанный с ней тип колебания струны называется нормальной модой. Наименьшая частота f₁ называется основной частотой, все остальные (f₂, f₃, …) называются гармониками. На рисунке 1 изображена нормальная мода для n = 2.

В стоячей волне нет потока энергии. Колебательная энергия, заключенная в отрезке струны между двумя соседними узлами, не транспортируется в другие части струны. В каждом таком отрезке происходит периодическое (дважды за период Т) превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Но в отличие от груза на пружине или маятника, у которых имеется единственная собственная частота

струна обладает бесчисленным количеством собственных (резонансных) частот f_n. На рисунке 2 изображены несколько типов стоячих волн в струне, закрепленной на обоих концах.

Рисунок 2 Гармоники

Скорость поперечных волн в натянутой струне или резиновом жгуте зависит от погонной массы μ (т. е. массы единицы длины) и силы натяжения T:

Методика измерений:

Запустите программу «Открытая физика 2.5 часть 1.». Выберите в разделе «Содержание» пункт 2.6 «Механические волны». Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект.

Перейдите от окна теории к окну модели, щелкнув по изображению «Модель. Нормальные моды струны». Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы.

Зарисуйте поле эксперимента и схему лабораторной установки. Изменяя значения регуляторов , T, и f, пронаблюдайте на экране колебания струны. Изменяя частоту, добейтесь явления резонанса.

Получите у преподавателя допуск для выполнения измерений.

Порядок измерений:

1. Установите значения погонной плотности струны и ее натяжения соответственно таблице 1 для вашей бригады.

ТАБЛИЦА 1. Погонная плотность струны (не перерисовывать)

Бригада	1	2	3	4	5	6	7	8
μ [г/м]	95	90	85	80	75	70	65	60
T[Н]	3.2	3.0	3.2	2.8	2.6	2.4	2.2	2.0

2. Изменяя значение частоты возбуждающей силы, найдите первую моду струны. Запишите найденное значение частоты в таблицу 2. Зарисуйте вид струны.

3. Проведите измерения частоты возбуждающей силы для следующих гармоник струны. Результаты записывайте в таблицу 2.

ТАБЛИЦА 2. Определение скорости нормальных колебаний струны при μ = ____ г/м, Т = _____ Н.

№	Профиль струны	f, Гц	n=2L/m,м	vn=nfn,м/c

4. Рассчитайте скорость звука в струне для разных гармоник. Результаты запишите в таблицу 2.

5. Выберите первое значение основной частоты струны, соответствующее значению силы натяжения струны для вашей бригады. Запишите эти значения в таблицу 3 и по этим значениям рассчитайте массу груза, подвешенного к одному концу струны и скорость распространения колебаний.

6. Рассчитайте теоретическое значение скорости распространения колебаний в струне по формуле

7. Выберите еще 4 произвольных значения силы натяжения струны и измерьте соответствующие частоты первой моды струны. Повторите расчеты пункта 6.

8. Определите погрешность между теоретическим и экспериментальным значениями скорости распространения колебаний в струне.

ТАБЛИЦА 3. Изучение зависимости скорости колебаний струны от силы натяжения

№ п/п	Масса груза, mi ,кг	Сила натяжения струны Fi, Н	Основная частота fi,Гц	Скорость распространения колебаний vi=2Lfi, м/с	Погреш­ность vi,м/c	Скорость распро­странения колебаний (теорет.) vi теор, м/с

Лабораторная работа № 2.

Определение скорости звука

Цель работы:

Определение скорости звука в воздухе.

Оборудование:

• генератор звуковых частот

• источник питания

• осциллограф

• динамик

• микрофон

• усилитель

• линейка

Основные понятия:

Звуковыми волнами или просто звуком принято называть волны, воспринимаемые человеческим ухом. Диапазон звуковых частот лежит в пределах приблизительно от 20 Гц до 20 кГц. Волны с частотой менее 20 Гц называются инфразвуком, а с частотой более 20 кГц – ультразвуком. Волны звукового диапазона могут распространяться не только в газе, но и в жидкости (продольные волны) и в твердом теле (продольные и поперечные волны). Однако волны в газообразной среде – среде нашего обитания – представляют особый интерес. Изучением звуковых явлений занимается раздел физики, который называют акустикой.

При распространении звука в газе атомы и молекулы колеблются вдоль направления распространения волны. Это приводит к изменениям локальной плотности ρ и давления p. Звуковые волны в газе часто называют волнами плотности или волнами давления.

Важной характеристикой звуковых волн является скорость их распространения. Она определяется инертными и упругими свойствами среды. Скорость распространения продольных волн в любой безграничной однородной среде определяется по формуле

где β – модуль всестороннего сжатия, ρ – средняя плотность среды.

Скорость звука в газе определяется формулой Лапласа:

где p – среднее давление в газе, ρ – средняя плотность, что коэффициент γ равен отношению теплоемкостей при постоянном давлении C_p и при постоянном объеме C_V. Для двухатомных газов γ = 1,4. Расчет скорости звука по формуле Лапласа дает значение υ = 332 м/с (при нормальных условиях).

Формулу Лапласа можно представить в другом виде, если воспользоваться уравнением состояния идеального газа:

где T – абсолютная температура, M – молярная масса, R = 8,314 Дж/моль·К – универсальная газовая постоянная. Скорость звука сильно зависит от свойств газа. Чем легче газ, тем больше скорость звука в этом газе. Так, например, в воздухе (M = 29·10^–3 кг/моль) при нормальных условиях υ = 331,5 м/с, в гелии (M = 4·10^–3 кг/моль) υ = 970 м/с, в водороде (M = 2·10^–3 кг/моль) υ = 1270 м/с.

В жидкостях и твердых телах скорость звуковых волн еще больше. В воде, например, υ = 1480 м/с (при 20 °С), в стали υ = 5–6 км/с.

Описание лабораторной установки

В основе измерения скорости звука лежит метод фигур Лиссажу.

На рисунке представлена схема лабораторной установки, в состав которой входят звуковой генератор (ЗГ), электронный осциллограф(ЭО) и цилиндрическая воздушная полость с линейной шкалой, внутри которой находятся динамик (Д) в качестве источника звуковых волн и микрофон(М) в качестве приемника и преобразователя звуковых колебаний в электрический сигнал. Микрофон может перемещаться внутри цилиндрической полости по отношению к динамику.

Звуковой генератор ЗГ вырабатывает переменное электрическое напряжение в диапазоне частот от 20 до 20000 Гц, к выходным клеммам ЗГ подсоединен динамик Д, преобразующий эти колебания в звук определенной частоты (тона) и интенсивности (громкости). Эти характеристики можно регулировать с помощью двух тумблеров на передней панели ЗГ. Звуковые волны, распространяющиеся от динамика преобразуются микрофоном М в электрические колебания той же частоты, но достигающие микрофона с запаздыванием на время t=x/v=Tx/λ. Этому времени соответствует разность фаз между колебаниями в микрофоне и в динамике, равная φ=2πx/λ. Если микрофон, начиная от места расположения динамика, перемещать вдоль шкалы x, то разность фаз будет меняться и через каждые повторяющиеся интервалы x=λ претерпевать изменения на 2π.

Таким образом, перемещая микрофон, мы фиксируем положения микрофона, при которых фаза колебаний отличается на 2 π, что соответствует расстоянию между этими точками равно длине волны λ. Наиболее удобно фиксировать форму фигуры Лиссажу в виде прямой, когда фазовый сдвиг кратен π.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. Внести технические данные приборов в табл. 1.

1.Проверить готовность установки к работе.

2.Включить тумблером “Сеть” ЭО и ЗГ, подождать 2-3 мин, пока приборы прогреются.

3.Получить синусоиду на экране ЭО, для чего:

а) на ЗГ установить ручкой “Частота” (смотреть на круговой лимб!) частоту v ~ 100 Гц. Ручкой “Peг. Выхода”,

вращая ее по часовой стрелке, установить напряжение не более 0,5 В;

б) на ЭО ручками “Усиление” (X и Y), “Диапазон частот” и “Частота плавно” (“Синхронизация - в положении

“Внутр.”!) добиться четкой синусоиды;

в) изменяя напряжение ручкой “Peг. Выхода”: на ЗГ, наблюдать изменение амплитуды на ЭО, а на слух -

изменение громкости звука;

г) изменяя частоту на ЗГ, наблюдать “сжатие” и “растяжение” синусоиды, а на слух - изменение высоты звука.

4. Установить ручки “Диапазон частот” и “Частота плавно” в положение

“Выкл.”, а “Синхронизация” в положение “Внешн.”. На ЗГ установить частоту ν (задает преподаватель!). При

этом на экране появится фигура Лиссажу.

5. Вращением моховичка К на установке добиться при положении риски вблизи левого конца шкалы вида (а) или

(б) (рис. 5). Зафиксировать положение риски на шкале X1.

6. Вращая К и пройдя через последовательность промежуточных фигур, вновь добиться вида (а). Зафиксировать

X2 и следующие Х3, Х4 (сколько уложится вдоль шкалы).

7. Проделать пункты 5 и 6 при других заданных частотах.

8. Рассчитать длины волн для каждой частоты как

1 2 1 1 Δx = x − x = λ и т.д.

2 3 2 2 Δx = x − x = λ

Данные измерения внести в таблицу.

9. Рассчитать скорость звуковой волны по формуле (3) и погрешности измерения.

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Дать понятие звуковой волны. Написать уравнение волны.

2. Дать понятие величин, характеризующих звук.

3. Как получаются фигуры Лиссажу в данной установке?

4. Чем обусловлен сдвиг фаз между колебаниями вдоль осей х и у?

5. Вычислите скорость звука в воздухе при условиях Вашего опыта по формуле (3), где μ = 29-10-3 кг/моль, а γ= 1,4.