Допускаемые максимальные напряжения изгиба

[σ_F]_max = σ_Flim·Y_Nmax·K_st/S_st , (3.8)

где Y_Nmax = 4 –предельное значение коэффициента долговечности; K_st = 1,3 - коэффициент учета частоты приложения пиковой нагрузки (Т_пик ) [2, с.183]; S_st = 2 – коэффициент запаса прочности [2, с.183].

Для шестерни [σ_F]_1max = 486·4·1,3/2 = 1263,6 МПа, для колеса [σ_F]_2max = 441·4·1,3/2 = 1146,6 МПа.

3.3. Проектный расчет

3.3.1 Межосевое расстояние

а_w = 0,85(u ± 1) 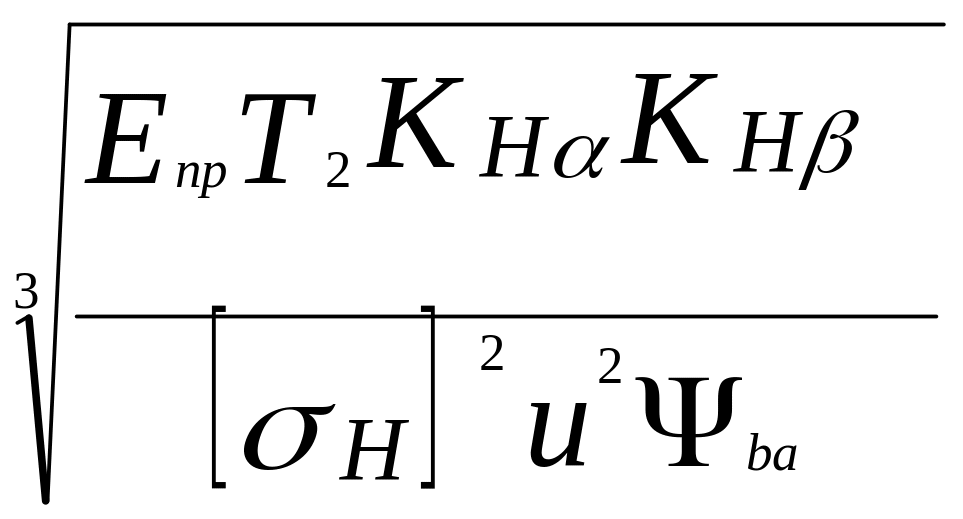, (3.9)

где Е_пр = 2,1· 10⁵ МПа; К_Нα = 1+ 0,06 (8 – 5) = 1,18 (<1,25) – см . [2 , с 133]; _ba = 0,315 ( табл.8. 4, [2 ]); К_Нβ =1,06 – рис. 8.15,график V при _bd = 0, 5 _ba ( u ± 1) = 0,5· 0,315 (4,26+1) = 0,83; [σ_Н] =509,1 МПа; Т₂ = 576,43 МПа.

Округляя по ряду принимаем .

3.3.2 Ширина венца колеса

b₂ = = 0,315· 210 = 66,15 мм. (3.10)

Принимаем b₂ = 65 мм.

3.3.3 Модуль зацепления

m = b₂/ _m = 65/25 = 2.6 мм, (311)

где = 25 согласно табл.8.5 [2 ]. Принимаем стандартный модуль m = 2,5мм.

3.3.4 Суммарное число зубьев колес

z₁ + z₂ = 2а / m = 2· 210 /2,5 =168. (3.12)

Тогда число зубьев шестерни z₁ = = 168/5.26 =31,93. Принимаем z₁ = 32> z_min = 17. Число зубьев колеса z₂ = - z₁ = 168- 32 =136.

Фактическое передаточное число u = z₂/ z₁ = 136/32 = 4,25. Отклонение величины u от заданной (u = 4,26) составляет [(4,26 – 4,25)/4,26]100% =0,23 %, что меньше допускаемого ± 4%.

3.3.5. Основные геометрические размеры шестерни и колеса:

делительный диаметр

d₁ = z₁m = 32· 2,5= 80 мм; (3.13)

d₂ = z₂m = 136· 2,5 = 340 мм, (3.14)

межосевое расстояние

а_w = (d₁ +d₂)/2 = (80 + 340)/2 = 210 мм; (3.15)

диаметр вершин зубьев

d_a1 = d₁ + 2m = 80 + 2· 2,5 = 85 мм; (3.16)

d_a2 = d₂ + 2m = 340 + 2· 2,5 = 345 мм;

ширина шестерни

b₁ = b₂ +(5…10) мм, (3.17)

принимаем b₁ = 70 мм.

3.3.6 Силы в зацеплении:

окружная сила

F_t = 2 T₁ /d₁ = 2· 128,45 10³ / 80 = 3211,32 Н (3.18)

радиальная сила

(3.19)

3.4.Проверочный расчет

3.4.1. Проверка зубьев по контактным напряжениям

Расчетное значение контактного напряжения

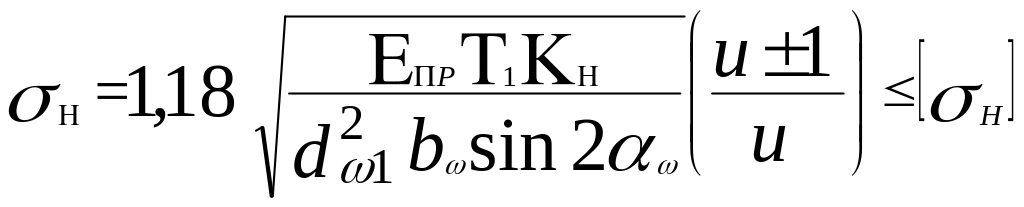. (3.20)

Здесь α_W = α =20⁰; sin2α = 0,6428; Для определения К_нυ необходимо предварительно определить скорость: v = πd₁n₁ /60 = 3.14 ·80· 10^-3 · 383,4 /60 =1.605 м/сек. По табл. 8.3 [2 ] для прямозубой передачи 8 – й степени точности при Н₁ <350 НВ и Н₂ < 350 НВ- К_Нv = 1,08. Раннее было определено К_Нα = 1,18; К_нβ =1,08.

Тогда

К_н = К_Нα · К_нβ · К_нυ = 1,18· 1,08· 1,08 = 1,38; (3.21)

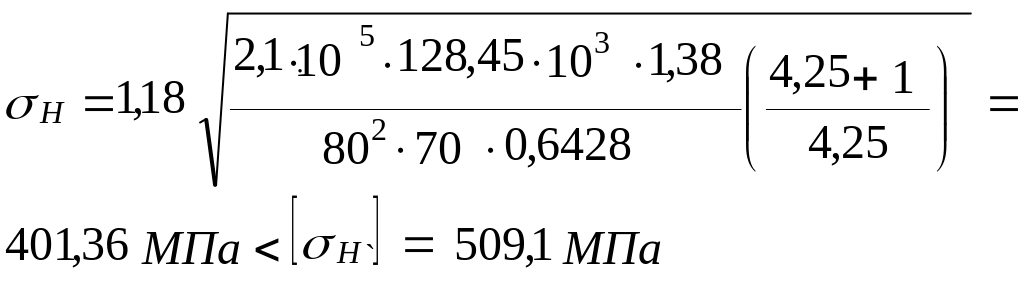
3.4.2. Проверка зубьев колес по напряжениям изгиба

Выполняем проверочный расчет на сопротивление усталости по напряжениям изгиба по формуле:

. (3.22)

По графику рис. 8.20 при х =0 [1] находим: для шестерни Y_FS1 = 3,85,

для колеса Y_FS2 = 3,75. Проверку выполняем по тому из колес пары, для которого меньше отношение: [σ_F] / Y_FS

Для шестерни [σ_F]₁ / Y_FS1 = 277,1/3,85 = 71,97; колеса - [σ_F]₂ / Y_FS2= 252/3,75 = 67,2, т.е. - по колесу.

По графику рис. 8.15, К_Fβ = 1,08 ( _bd = 0,826; график V); по табл. 8.3 К_FV = 1,16. Коэффициент расчетной нагрузки при К_Fα = К _Нα = 1,18: К_F = 1,18· 1.08· 1.16 = 1.48.

Тогда

σ_F = 3.75· 1,48· 3211,32/ 65 2,5 = 109,67 МПа< [σ_F]₂ = 252 МПа.- условие прочности выполняется.

3.4.3. Проверка прочности зубьев при перегрузках

Максимальные контактные напряжения

(3.23)

Максимальные напряжения изгиба

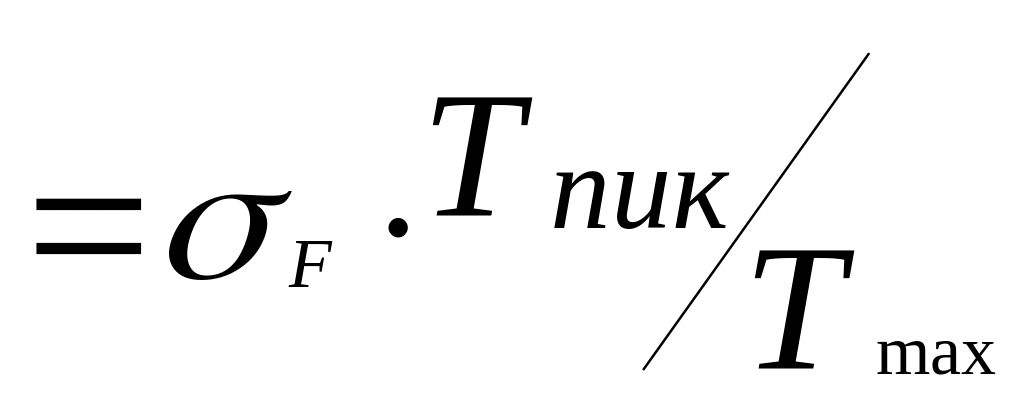
(3.24)