Лабораторна робота №1 4

Тема: Експериментальне оцінювання закону розподілу вимірювань. Застосування різних видів аналізу для визначення інформаційних характеристик. 4

Мета: роботи: 4

ЗАГАЛЬНІ ТЕОРЕТИЧНІ ВІДОМОСТІ 4

Завдання на лабораторну роботу. 16

Порядок виконання роботи 17

Контрольні запитання 19

Додаток 1.1 20

Скрипт для генерації вихідних даних 20

Лабораторна робота №1 Тема: Експериментальне оцінювання закону розподілу вимірювань. Застосування різних видів аналізу для визначення інформаційних характеристик.

Мета: роботи:	Набути навичок обробки експериментальних даних вимірювань

Загальні теоретичні відомості

МЕТОДИ ОТРИМАННЯ ОЦІНОК

Кількісні значення оцінок шуканих величин у загальному випадку є функціями елементів вибірки. Для знаходження алгоритмів обчислення оцінок найбільш широке поширення одержали наступні методи: максимальної правдоподібності, моментів, порядкових характеристик і Байеса.

МЕТОД НАЙМЕНШИХ КВАДРАТІВ

У ряді випадків механізм формування похибок полягає в підсумовуванні великої кількості елементарних складових із приблизно однаковими дисперсіями, що дозволяє припустити нормальність розподілу. Застосування методу максимальної правдоподібності до знаходження невідомих параметрів при нормальному законі розподілу похибок приводить до певної обчислювальної схеми — методу найменших квадратів (МНК). Ця схема є досить простою, тому МНК найчастіше застосовують і в тих випадках, коли похибки вимірювань не підкоряються нормальному закону. Одержувані при цьому квазіподобні оцінки мають меншу в порівнянні з оцінками максимальної правдоподібності точність. МНК зручний також тим, що дозволяє легко організувати рекурентні схеми обчислень, у яких одержання кожного нового вимірювання викликає уточнення колишньої оцінки.

Математична модель при багатомірних вимірюваннях:

де — шукані величини; — величини, доступні для вимірювання в процесі експерименту; — вимірювання величина, щодо якої функціонал розв’язується в явному вигляді:

При вимірювані N параметрів кожне опосередковане вимірювання зв'язано відомою залежністю із сукупністю параметрів, що нас цікавлять, і виміряними значеннями:

де — результат i-го вимірювання, що містить випадкову похибку ;

- відома функція від невідомих параметрів; — нев’язка і-го вимірювання, причому в рівняння з експериментальними даними замість дійсних значень параметрів входять їхні оцінки. З метою спрощення записів вони не символізовані. Сукупність усіх рівнянь складає фундаментальну систему несумісних рівнянь. Оскільки точність окремих вимірювань може бути різною, тобто кожному рівнянню можна приписати ваговий коефіцієнт .

Оцінками, які отримують методом найменших квадратів ( МНК-оцінками), називають сукупність оцінок, що мінімізують зважену суму квадратів нев’язок:

Для мінімізації функціонала необхідно його продиференціювати по всіх змінних і частинні похідні прирівняти до нуля:

Отриману в такий спосіб систему N рівнянь із N невідомими називають системою нормальних рівнянь. Можливість складання такої системи зв'язана тільки з диференціюванням функції і не залежить від їхньої лінійності. Однак при нелінійній залежності розв'язання системи нормальних рівнянь пов'язане з великими обчислювальними труднощами й може бути неоднозначним, тому їх попередньо необхідно лінеаризувати. Це досягається розкладом функції у ряд Тейлора в околі нульового наближення з подальшим обмеженням лінійними членами, щодо шуканих параметрів. Рівняння фундаментальної системи в цьому випадку приймає вид

Для скорочення записів введемо наступні позначення:

З урахуванням прийнятих позначень запишемо і-е рівняння фундаментальної системи:

Сума квадратів нев’язок рівна

Для одержання системи нормальних рівнянь функціонал Q диференціюється по кожній змінній й отримані частині похідні прирівнюються до нуля. У результаті одержимо:

Після найпростіших перетворень система набуває вигляду:

Подальший опис і аналіз методу найменших квадратів зручніше проводити в матричній формі. Позначимо вектор початкових наближень , вектор вимірювань X, вектор обчислень значень вимірюваної величини , вектор нев’язок , матрицю коефіцієнтів лінеаризованої фундаментальної системи рівнянь , діагональну матрицю вагових коефіцієнтів і шуканий вектор оцінок , тобто:

Тоді фундаментальну систему лінеаризованих рівнянь можна записати компактно в матричній формі:

Система нормальних рівнянь:

Позначивши квадратну матрицю коефіцієнтів системи нормальних рівнянь і , маємо

Перемножуючи обидві сторони системи на зворотну матрицю , одержуємо матрицю оцінок:

Якщо результати вимірювань корельовані, а кореляційна матриця то матриця вагових коефіцієнтів повинна бути . При цьому кореляційна матриця оцінок .

ОЦІНКА МАТЕМАТИЧНОГО СПОДІВАННЯ

Координата центру розподілу визначає положення щільності розподілу на числовій осі. Можливі різні визначення поняття центру розподілу. Як правило, за центр розподілу ухвалюють центр ваги однорідної плоскої фігури, обмеженою щільністю розподілу, тобто перший початковий момент, або математичне сподівання. Однак для гостровершиних розподілів, близьких до розподілу Коші і таких, що не мають моментів, поняття математичного сподівання не має змісту. У таких випадках у якості характеристики положення можна прийняти центр симетрії як точку на осі, ліворуч і праворуч від якої поява випадкової величини рівноймовірна і становить 0,5. Згідно з визначенням, — це медіана. Крім того, такою характеристикою можуть бути центр розмаху, середина інтерквантильного проміжку й ін., що існують для будь-яких розподілів. Проте для розподілів, що мають моменти розподілів (такі розподіли зустрічаються на практиці найчастіше), у більшості випадків в якості оцінки центру розподілу найчастіше використовують математичне сподівання (генеральне середнє). Особливо велика роль середнього при обробці результатів вимірювання, тому що воно збігається із шуканим значенням.

Оцінкою максимальної правдоподібності математичного сподівання нормального закону є середнє арифметичне, що збігається з оцінкою по методу моментів незалежно від закону розподілу. Середнє арифметичне — незміщена оцінка для будь-якого розподілу, тому що математичне сподівання дорівнює дійсному значенню:

Дисперсія середнього арифметичного:

Порівняння з оптимальною оцінкою показує, що середнє арифметичне — ефективна оцінка математичного сподівання нормальної сукупності. Середньо квадратичне відхилення результату вимірювання:

Таким чином, випадкова величина має середнє значення т і стандартне відхилення . Якщо середнє арифметичне отримане по вибірці з нормальної сукупності, те завдяки стійкості нормального закону (сума нормально розподілених випадкових величин є нормальною) воно розподілене також за нормальним законом. У випадку генеральної сукупності, відмінної від нормальної, згідно із граничною теоремою Ляпунова середнє арифметичне асимптотично нормально.

Застосуємо метод максимальної правдоподібності для одержання оцінки математичного сподівання сукупності з експоненціальним розподілом (розподілом Лапласа):

Функція правдоподібності:

За загальним правилом одержання оцінок максимальної правдоподібності одержимо:

Звідси знаходимо , тобто оцінкою математичного сподівання розподілу Лапласа є вибіркова медіана (середній член варіаційного ряду при непарному обсязі вибірки або напівсума середніх членів при парному n):

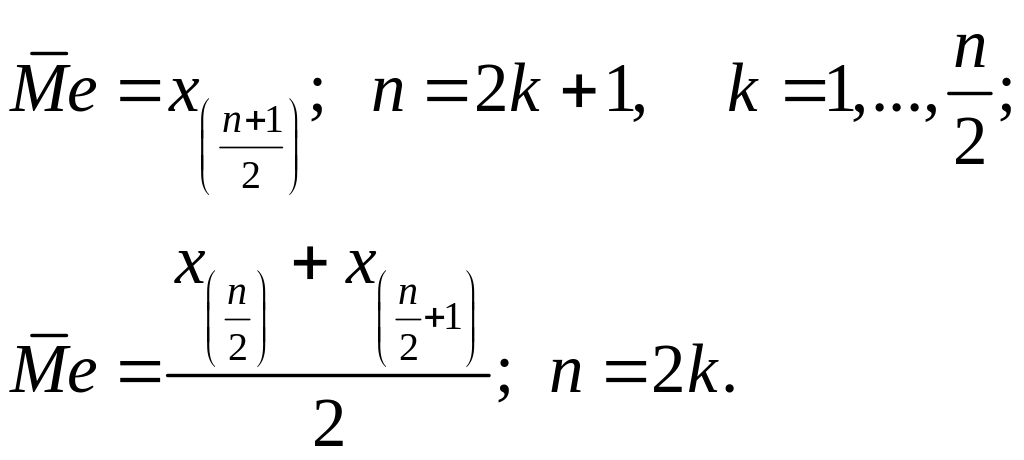
Вибіркова медіана являє собою оцінку квантиля порядку 0,5 по методу порядкових характеристик, а середній член варіаційного ряду є незміщеною оцінкою медіани. Для симетричних законів розподілу, для яких середнє значення й медіана збігаються, вибіркова медіана — незміщена оцінка математичного сподівання. Для несиметричних розподілів вона стає зміщеною оцінкою середнього значення. У загальному випадку вибіркова медіана асимптотично нормальна із середнім значенням, рівним дійсному значенню медіани, і середнім квадратичним відхиленням:

де — щільність розподілу в точці, рівній значенню медіани. Дисперсію оцінки медіани можна знайти з наступного рівняння:

Наприклад, для розподілу Лапласа — дисперсія оцінки медіани буде рівна

При малих п можна одержати краще наближення для дисперсії вибіркової медіани заміною члена в членом , де

Дисперсія вибіркової медіани у два рази менше дисперсії середнього арифметичного. Це означає, що вона є більш ефективною оцінкою математичного сподівання для експонентного розподілу в порівнянні із середнім арифметичним. Знайдемо мінімально можливе значення дисперсії математичного сподівання для розподілу Лапласа по нерівності Рао‑Крамера :

Порівняння з виразом показує, що вибіркова медіана — ефективна оцінка математичного сподівання для розподілу Лапласа.

Розглянемо оцінку максимальної правдоподібності математичного сподівання рівномірного закону розподілу шириною . Так як функція правдоподібності — добуток обмежених розподілів елементів вибірки, то вона постійна й відмінна від нуля в інтервалі , де — крайні члени варіаційного ряду. Максимум функції правдоподібності — у середині зазначеного інтервалу. Звідси виходить найпростіша оцінка математичного сподівання у вигляді центру розмаху крайніх членів варіаційного ряду:

Оцінка є незміщеною для симетричних законів розподілу. Вона виявляється досить ефективною для обмежених (рівномірного, трапецієподібного й ін.), а також антимодальних (розподіл арксинуса) і двухмодальних розподілів. Дисперсія оцінки визначається спільним розподілом крайніх членів вибірки, тому знаходження її в загальному виді досить важке.

У табл. 1.1 наведені дисперсії й порівняльні ефективності оцінок для широкого класу типових законів розподілу випадкових величин і похибок, що найбільше часто зустрічаються у вимірювальній практиці.

На рис. 1.1 показані приблизні графіки ефективності цих оцінок залежно від форми законів розподілу, систематизованних за значенням контрексцесса . Ефективність оцінок залежить як від форми розподілу, так і від обсягу вибірки.

Таблиця 1.1. Порівняння ефективності

оцінок математичного сподівання

Закон розподілу	Контрексцесс
Лапласа	0,408				----
Нормальний	0,577
Трикутний (Сімпсона)	0,645
Рівномірний	0,745
Арксинуса	0,816

Ефективність вибіркової медіани падає з ростом контрексцеса розподілу, тобто зі зменшенням гостровершиності, і перетинає одиницю при . Ефективність центру розмаху, навпаки, зростає, причому досить швидко й суттєво залежить від обсягу вибірки, особливо у випадку антимодальних розподілів, і для п = 20 досягає одиниці при , а для гостровершиних розподілів стає неспроможною (розподіл Лапласа).

В області законів розподілу, близьких до нормального ( ), кращою оцінкою математичного сподівання є середнє арифметичне, для гостровершиних розподілів більш ефективною оцінкою стає вибіркова медіана, для плосковершиних і антимодальних — центр вибіркового розмаху. Ріст ефективності оцінки означає виграш в обсязі вибірки при заданій однаковій точності вимірювання.

Рис.1.1. Порівняння ефективності оцінок математичного сподівання

Порівнюючі різні оцінки центру розподілу, необхідно, крім їхньої ефективності (значення дисперсії), ураховувати чутливість до промахів (у загальному випадку різко відмінним від основної сукупності спостережень результатом, що належать до іншої генеральної сукупності). Оцінка у вигляді центру розмаху винятково чутлива до промахів, тому що вона визначається тільки по найбільш віддалених від центру результатах, якими промахи і є. Середнє арифметичне також слабко захищене від впливу промахів: воно послабляється лише в п раз. Стійкими до промахів є квантильні оцінки, у першу чергу вибіркова медіана. Для зниження впливу промахів на результати виміру застосовують різні способи редагування (цензурування) вибірки, включаючи двоступінчасту процедуру з попереднім виявленням і виключенням промахів. Найпростіший спосіб — усікання вибірки, тобто виключення з вибірки по т (наприклад, по 5 % від загального обсягу) крайніх членів вибірки. Усічене середнє арифметичне рівно

Усічений вибірковий центр розмаху

Для симетричних двухмодальних розподілів усічений вибірковий розмах доцільно обчислювати як напівсуму оцінок квантилей порядку 0,25 і 0,75, котрі називають центром згинів:

ОЦІНКАДИСПЕРСІЇ

Ширина розподілу — узагальнена характеристика розсіювання випадкової величини відносно свого центру, у загальному випадку визначається як функціонал від щільності розподілу. У якості характеристики розсіювання для розподілів, що мають моменти, звичайно у квадратичній мірі приймається дисперсія, а в лінійній — середнє квадратичне відхилення. Крім того, для будь-яких розподілів, у тому числі, що й не мають моментів, мірою розсіювання є ймовірне відхилення, середнє відхилення по модулю, довжина інтерквантильного проміжку й ін. Розглянемо оцінку дисперсії й середнього квадратичного відхилення, тобто припустимо існування другого центрального моменту. Оцінкою максимальної правдоподібності дисперсії нормальної сукупності при невідомому математичному сподіванні служить статистика:

При відомому математичному сподіванні т оцінка дисперсії незміщена. Незміщену оцінку дисперсії позначимо

Обидві оцінки є оцінками другого центрального моменту для довільних законів розподілу. Математичне сподівання вибіркової дисперсії знаходимо з рівняння :

Додаючи й віднімаючи , після піднесення в квадрат і обчислення математичних сподівань доданків, що утворювалися, одержуємо:

Перший доданок — дисперсія генеральної сукупності, друге — дисперсія середнього арифметичного. Таким чином,

Отже, вибіркова дисперсія — зміщена оцінка дисперсії. При великих зсув незначний і ним можна знехтувати, а при малих обсягах вибірки слід використовувати незміщену оцінку:

Оцінка дисперсії середнього арифметичного:

Мінімально можливе значення дисперсії оцінки дисперсії нормальної сукупності при заданому обсязі вибірки може бути знайдене по нерівності Рао‑Крамера:

Знайдемо дисперсії оцінок і (при відомому і невідомому математичному сподіванні):

Аналогічним чином знаходимо дисперсії оцінок середнього квадратичного відхилення при відомому і невідомому математичному сподіванні:

Звідси відносні значення похибок оцінок середнього квадратичного відхилення відповідно рівні

З іншого боку, дисперсія оцінки дисперсії для довільних законів розподілу може бути знайдена за загальним правилом обчислення дисперсії випадкової величини як функції випадкових аргументів (елементів вибірки). Дисперсія зміщеної оцінки матиме вигляд

де — четвертий центральний момент; — дисперсія.

Для отримання дисперсії незміщеної оцінки дисперсії досить, як видно з рівняння , помножити вираз на .

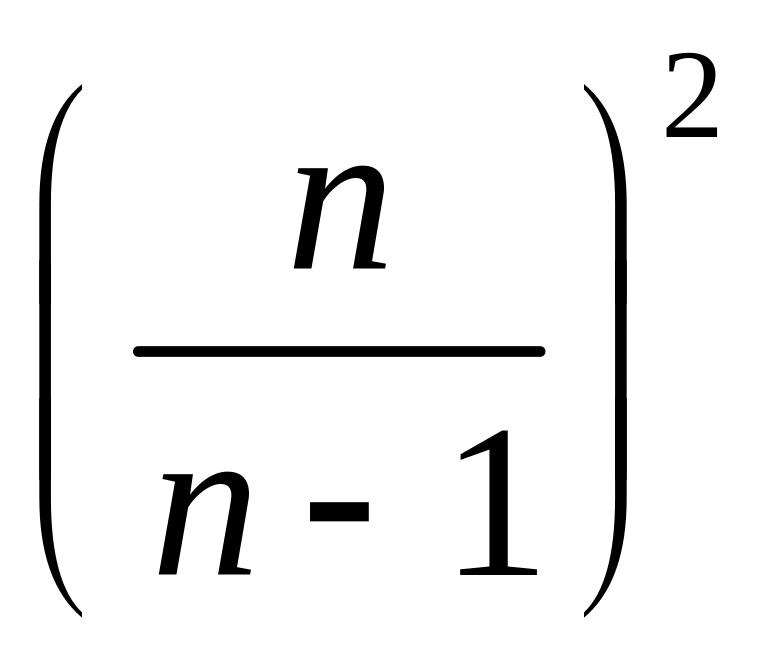Якщо знехтувати другим і третім доданком , які є величинами другого порядку малості в рівнянні, що цілком припустимо при досить великому обсязі вибірки ( при п > 20 похибка не перевищує 10%), одержимо

Дисперсію оцінки середнього квадратичного відхилення легко одержати з рівняння . Для оцінки виразу п—1 заміняємо на п:

З рівнянь і випливає, що відносна похибка оцінок залежить тільки від обсягу вибірки й виду розподілу (ексцесу ) і не залежить від , тобто точності, з якою виконано вимірювання (вона може бути зменшена тільки шляхом збільшення обсягу вибірки):

Враховуючи, що для нормального закону , дисперсії виразів і збігаються з результатами рівнянь і , що випливають із нерівності Рао-Крамера. Останнє означає ефективність цих оцінок для нормального закону розподілу. При обсязі вибірки п < 50, як видно з виразу , середнє квадратичне значення похибки оцінки середнього квадратичного відхилення становить не менш 10%.

Для експоненціального розподілу оцінка максимальної правдоподібності середнього квадратичного відхилення може бути знайдена за загальним правилом :

Аналогічним чином виходить, що оцінкою дисперсії буде статистика (нелінійне перетворення приводить до зсуву):

З виразу безпосередньо видно, що оцінка незміщена, тому що , а , тобто . Оцінимо зміщеність оцінки дисперсії :

Отже, оцінка дисперсії рівняння є зміщеною. Незміщену оцінку знаходимо множенням дисперсії зміщеної оцінки на множник

Дисперсія оцінки середнього квадратичного відхилення з врахуванням рівності приймає вигляд:

З порівняння дисперсій виразів і видно що оцінка рівняння ефективніше оцінки , чим пояснюється її широке застосування незалежне від виду розподілу.

Можливі й інші види оцінок дисперсії й середнього квадратичного відхилення. Наприклад, остання для рівномірного закону розподілу може бути прийнята у вигляді про (така оцінки однак по якості поступається класичним оцінкам виду ).