Лабораторная работа №13 Исследование фильтров

Цель работы - изучение основных характеристик амплитудно-частотных (АЧХ) и фазо-частотных (ФЧХ) характеристик фильтров первого и второго порядков.

Задание:

1. Провести расчет АЧХ и ФЧХ фильтра первого порядка в диапазоне частот 0,1...100 кГц и сравнить их с результатами моделирования.

2. Для фильтра второго порядка рассчитать АЧХ и ФЧХ в диапазоне частот 30...300 Гц и сравнить их с результатами моделирования.

3. Провести моделирование активного RC-фильтра. Установить зависимость АЧХ фильтра от сопротивления резисторов и границы устойчивой работы схемы, изменяя сопротивление.

Методическое указание к выполнению работы.

Краткие сведения из теории.

Фильтрующие элементы используются в блоках питания для фильтрации сигналов, в качестве корректирующих звеньев в системах управления и т.п. Фильтры делятся на два больших класса — пассивные и активные, причем основным отличием активного фильтра является наличие усилительного элемента — обычно это ОУ. Если в фильтре содержится один реактивный элемент (емкость или индуктивность), то такой фильтр называется фильтром первого порядка, если два — то второго порядка, и т.д.

Наиболее распространенным пассивным фильтром первого порядка является интегрирующая RC-цепь, входящая в состав рассмотренного выше интегратора, который может рассматриваться как активный низкочастотный фильтр первого порядка. Этот же фильтр в технике электропитания называется Г-образным, в аудиотехнике — фильтром нижних частот (ФНЧ), а в технике управления — корректирующим или интегрирующим звеном. Основными характеристиками фильтра являются АЧХ и ФЧХ, для интегрирующей цепи на рис. 13.1 они описываются выражениями:

Следует отметить, что фильтры на базе RC-цепей обладают своеобразной дуальностью. Если на рис. 13.1 поменять местами элементы R и С, то получим фильтр верхних частот (ФВЧ).

Классической схемой фильтра второго порядка является последовательная RLC-цепь (рис. 13.2).

Если выходной сигнал измерять на конденсаторе, получим ФНЧ, а если на индуктивности L — ФВЧ. RLC-цепь обладает явными резонансными свойствами, ее АЧХ и ФЧХ описываются выражениями:

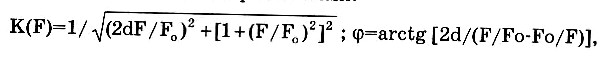
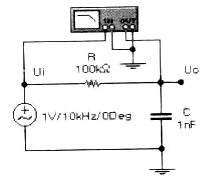
Рис. 13.1

где d=R/2√C/L — коэффициент затухания, его обратная величина называется добротностью Q=l/d, часто определяемой как Q=F/AF, где AF — ширина полосы пропускания по уровню 0,707 (-3 дБ); Fo=1/(2π√LC) - резонансная частота.

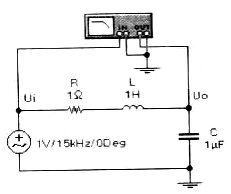
Рис. 13.3

При практической реализации RLC-фильтров (особенно низкочастотных) наибольшие трудности возникают с изготовлением катушек индуктивности, их экранированием, а при больших значениях индуктивности — с проблемой массы и геометрических размеров. Эти проблемы были решены с использованием активных RC-фильтров, называемые безындуктивные частотные фильтры на базе операционных усилителей. На рис. 10.3 приведена схема активного ФНЧ второго порядка на ОУ.

Из полосовых фильтров наибольшее распространение получили фильтры, АЧХ которых описывается полиномами Баттерворта, Чебышева и Бесселя.

Фильтры Баттерворта характеризуются максимально плоской АЧХ в полосе пропускания. Управление величиной выходного напряжения и перестройка по частоте в широком диапазоне осуществляются в этих фильтрах проще, чем в других фильтрах, поскольку при каскадном соединении все секции настраиваются на одну и ту же частоту.

Рис. 13.3

Фильтры Чебышева обеспечивают наивысшую крутизну АЧХ в переходной полосе частот. Однако при этом АЧХ в полосе пропускания приобретает колебательный характер. Чем больше неравномерность в полосе пропускания, тем выше крутизна затухания в переходной полосе частот.

Фнльтры Бесселя обладают максимально плоской характеристикой группового времени запаздывания (производная от ФЧХ по частоте) и линейностью ФЧХ в полосе пропускания. Однако крутизна затухания фильтра невелика.

Порядок выполнения рабочего задания

1. Собрать схему, представленную на рис. 13.1. Меняя параметры R и C получить характеристики фильтра и оценить влияние данных параметров на работу фильтра. Получить и зарисовать характеристики. Провести расчет АЧХ и ФЧХ фильтра в диапазоне частот 0,1...100 кГц и сравнить их с результатами моделирования.

2. Собрать схему, представленную на рис. 13.2. Меняя параметры R, L и C получить характеристики фильтра и оценить влияние данных параметров на работу фильтра. Получить и зарисовать характеристики. Рассчитать АЧХ и ФЧХ в диапазоне частот 30...300 Гц и сравнить их с результатами моделирования.

3. Провести моделирование активного RC-фильтра (рис. 13.3) Установить зависимость АЧХ фильтра от сопротивления резисторов R2 и R3 и границы устойчивой работы схемы, изменяя сопротивление R7=15 кОм.

Контрольные вопросы:

1. Что такое децибел?

2. Как определить коэффициент затухания?

3. В чем отличие RC фильтров от LC?

4. Преимущества и недостатки фильтров Баттерворта, Чебышева и Бесселя. Где используются?