
Построение vecm модели
Модель исправления ошибки в общем случае имеет следующий вид:
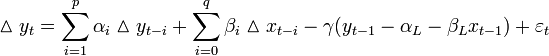
По байесовским информационным критериям Акаике, Шварца и Хеннана-Куинна наилучшей является модель с трендом в коинтегрирующем векторе. Лаг возьмем равным 17, так как он являлся наилучшим для модели VAR. Для построения модели выполним действия: Модель -> Временные ряды -> Векторная модель коррекции ошибок (VECM)… В появившемся диалоговом окне заносим в окно «Эндогенные переменные» исследуемые переменные, выбираем флажок «Включить константу». Вводим максимальный порядок лага 17. При построении получили следующий результат:
VECM система, порядок лага 17
Метод оценки - Максимальное правдоподобие, наблюдения 2000:06-2011:01 (T = 128)
Ранг коинтеграции = 1
Вариант 4: Ограниченный тренд, неограниченная константа
beta (Коинтегрирующие векторы, в скобках указаны стандартные ошибки)
v1 1,0000
(0,00000)
v2 -0,15604
(0,0073168)
trend -7,7433
(0,87831)
alpha (Корректирующие векторы)
v1 -0,67299
v2 1,2077
Лог. правдоподобие = -1558,3501
Определитель ковариационной матрицы = 1,2876062e+008
Крит. Акаике = 25,4430
Крит. Шварца = 27,0027
Крит. Хеннана-Куинна = 26,0767
Уравнение 1: d_v1
|
Коэффициент |
Ст. ошибка |
t-статистика |
P-значение |
|
const |
80,0277 |
21,3493 |
3,7485 |
0,00031 |
*** |
d_v1_1 |
0,139488 |
0,141073 |
0,9888 |
0,32534 |
|
d_v1_2 |
0,109904 |
0,120964 |
0,9086 |
0,36593 |
|
d_v1_3 |
0,270449 |
0,113632 |
2,3800 |
0,01935 |
** |
d_v1_4 |
0,195261 |
0,0982786 |
1,9868 |
0,04989 |
** |
d_v1_5 |
0,227961 |
0,0876238 |
2,6016 |
0,01080 |
** |
d_v1_6 |
0,093046 |
0,0882547 |
1,0543 |
0,29448 |
|
d_v1_7 |
0,12332 |
0,0873594 |
1,4116 |
0,16139 |
|
d_v1_8 |
-0,103242 |
0,0924408 |
-1,1168 |
0,26694 |
|
d_v1_9 |
-0,0175745 |
0,108773 |
-0,1616 |
0,87199 |
|
d_v1_10 |
-0,0519699 |
0,102491 |
-0,5071 |
0,61331 |
|
d_v1_11 |
0,137369 |
0,103127 |
1,3320 |
0,18610 |
|
d_v1_12 |
0,33025 |
0,107672 |
3,0672 |
0,00283 |
*** |
d_v1_13 |
0,420081 |
0,112586 |
3,7312 |
0,00033 |
*** |
d_v1_14 |
0,31926 |
0,121665 |
2,6241 |
0,01016 |
** |
d_v1_15 |
0,148554 |
0,126788 |
1,1717 |
0,24432 |
|
d_v1_16 |
0,0517772 |
0,111158 |
0,4658 |
0,64245 |
|
d_v2_1 |
-0,154437 |
0,0548732 |
-2,8144 |
0,00596 |
*** |
d_v2_2 |
0,0127099 |
0,0630252 |
0,2017 |
0,84062 |
|
d_v2_3 |
0,0593232 |
0,0643304 |
0,9222 |
0,35883 |
|
d_v2_4 |
-0,172432 |
0,0604857 |
-2,8508 |
0,00537 |
*** |
d_v2_5 |
-0,112778 |
0,0627129 |
-1,7983 |
0,07537 |
* |
d_v2_6 |
-0,0812268 |
0,0587712 |
-1,3821 |
0,17026 |
|
d_v2_7 |
-0,0317151 |
0,0576134 |
-0,5505 |
0,58331 |
|
d_v2_8 |
-0,102727 |
0,0573495 |
-1,7912 |
0,07651 |
* |
d_v2_9 |
-0,176603 |
0,0611174 |
-2,8896 |
0,00480 |
*** |
d_v2_10 |
-0,115364 |
0,0617434 |
-1,8684 |
0,06485 |
* |
d_v2_11 |
-0,208306 |
0,0577069 |
-3,6097 |
0,00050 |
*** |
d_v2_12 |
-0,206562 |
0,0620743 |
-3,3277 |
0,00126 |
*** |
d_v2_13 |
0,0685135 |
0,0746665 |
0,9176 |
0,36121 |
|
d_v2_14 |
-0,247306 |
0,0760563 |
-3,2516 |
0,00160 |
*** |
d_v2_15 |
0,194039 |
0,0782939 |
2,4783 |
0,01500 |
** |
d_v2_16 |
-0,186162 |
0,080941 |
-2,3000 |
0,02369 |
** |
EC1 |
-0,672986 |
0,141199 |
-4,7662 |
<0,00001 |
*** |
Среднее зав. перемен |
27,30609 |
|
Ст. откл. зав. перемен |
214,5158 |
Сумма кв. остатков |
890928,8 |
|
Ст. ошибка модели |
97,87686 |
R-квадрат |
0,847552 |
|
Испр. R-квадрат |
0,791819 |
Параметр rho |
-0,020826 |
|
Стат. Дарбина-Вотсона |
2,037040 |
