
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования –
Национальный исследовательский университет
«Нижегородский государственный университет им. Н.И. Лобачевского»
(ННГУ)
Механико-математический факультет
Кафедра математического моделирования экономических систем
Отчет по эконометрике
Исполнители:
магистранты 1 курса Батарина А.В.
Гнатюк А.А.
Лебедева Е.Г.
Наугольнова М.А.
Соловьева К.Ю.
Проверила: Буреева Н.Н.
Нижний Новгород, 2013 год
Исходные данные
Для анализа были взяты следующие временные ряды данных:
vvp – данные по ВВП (оценка Минфина РФ), млрд. руб.,
den_mass – объем денежной массы, млрд. долл.
(данные взяты с 1 января 1999 года по 1 января 2011 года по месяцам).
Полный обзор данных приведен в приложении.
Тестирование на стационарность
Рисуем график: Вид –График –График временного ряда.
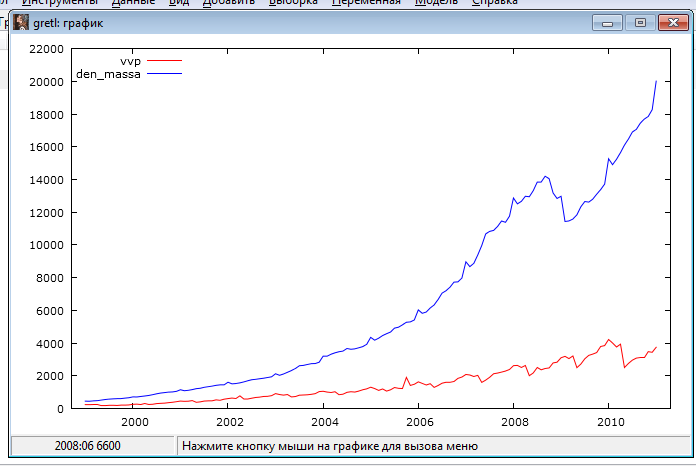
По графику можно предположить, что обе переменные будут нестационарными временными рядами.
Для анализа исходных данных нам понадобятся следующие таблицы:
Критические значения статистики Дики-Фуллера при 1%-ном уровне значимости
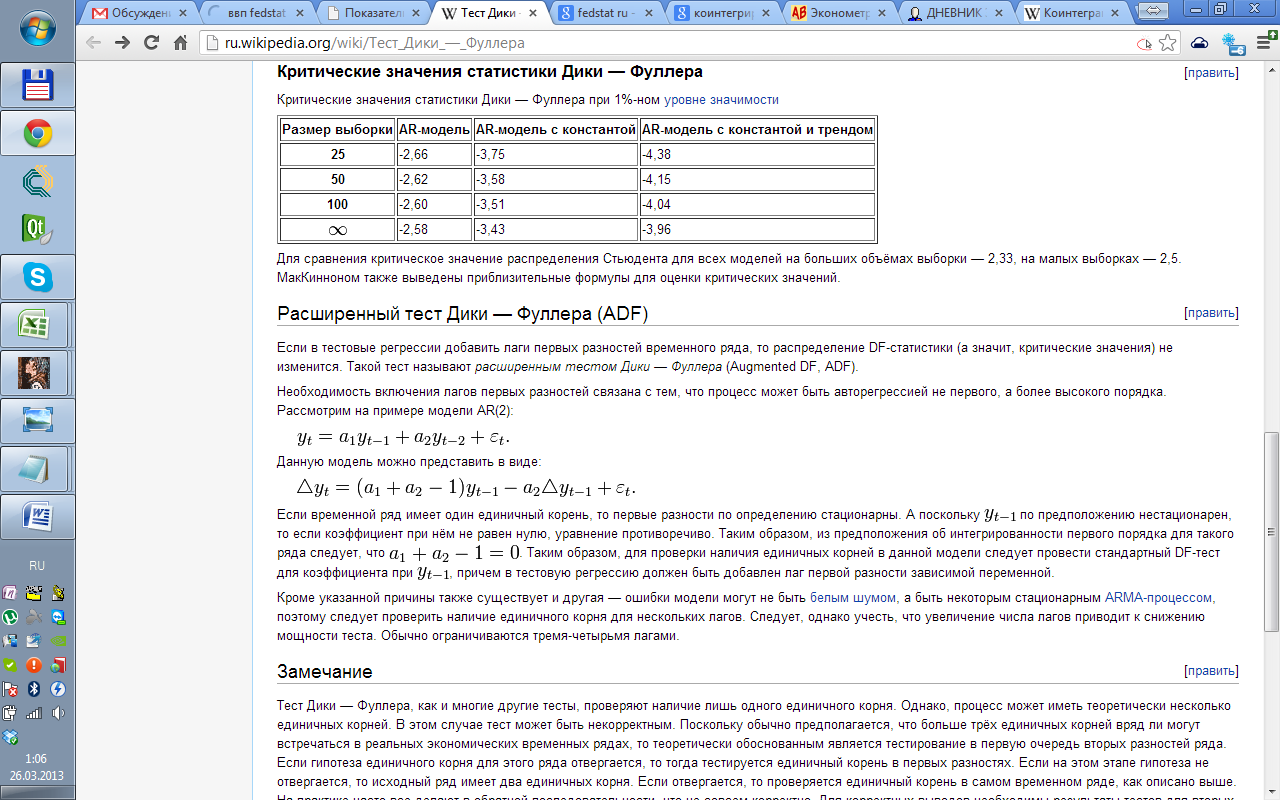
А также статистики для теста Энгла-Гренджера
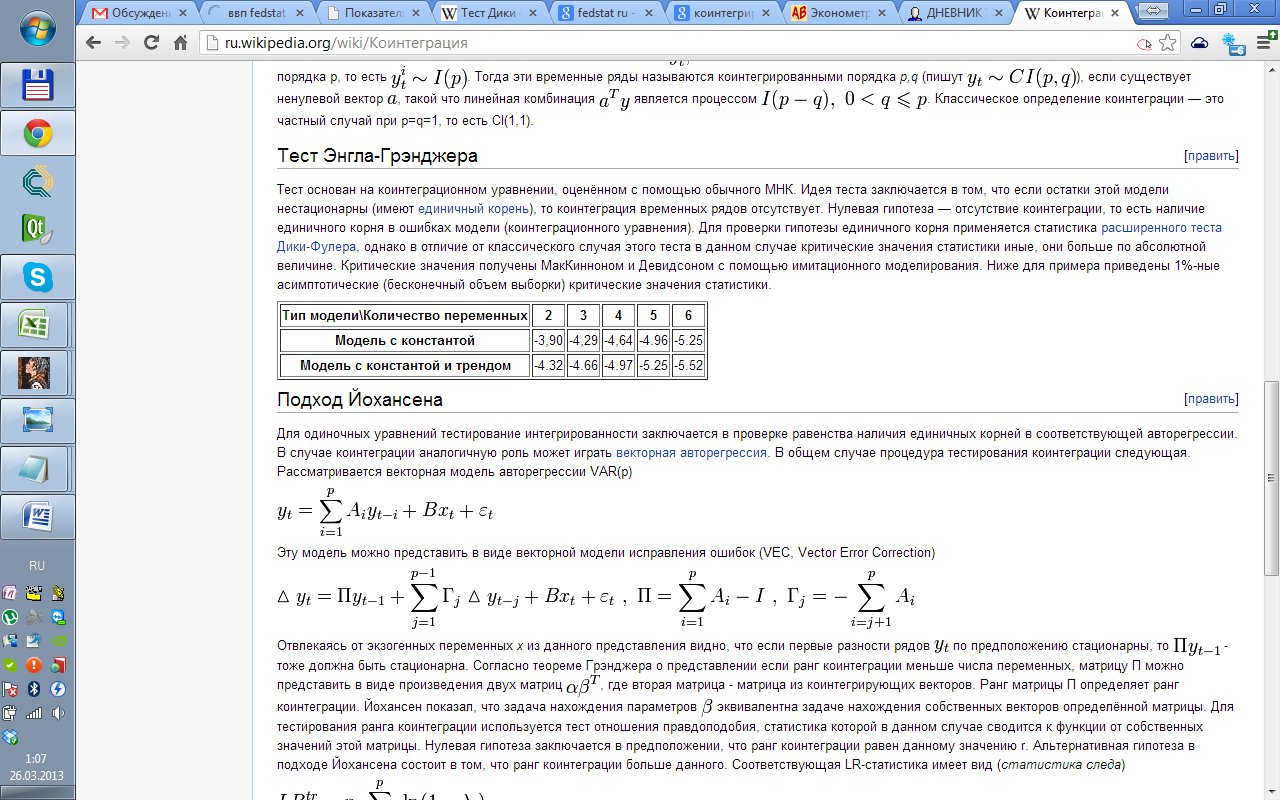
Тест проводится командами: Переменная - Тесты единичного кореня- Расширенный тест Дики-Фуллера.
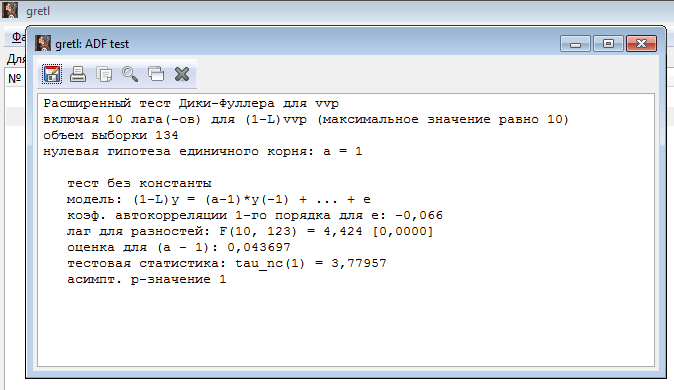
Расширенный тест Дики-Фуллера для vvp (используя уровень переменной)
включая 10 лага(-ов) для (1-L)vvp (максимальное значение равно 10)
объем выборки 134
нулевая гипотеза единичного корня: a = 1
тест без константы
модель: (1-L)y = (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: -0,066
лаг для разностей: F(10, 123) = 4,424 [0,0000]
оценка для (a - 1): 0,043697
тестовая статистика: tau_nc(1) = 3,77957
асимпт. р-значение 1
тест с константой
модель: (1-L)y = b0 + (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: -0,075
лаг для разностей: F(10, 122) = 4,665 [0,0000]
оценка для (a - 1): 0,0207853
тестовая статистика: tau_c(1) = 1,24995
асимпт. р-значение 0,9985
с константой и трендом
модель: (1-L)y = b0 + b1*t + (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: -0,075
лаг для разностей: F(10, 121) = 3,408 [0,0006]
оценка для (a - 1): -0,103023
тестовая статистика: tau_ct(1) = -1,62982
асимпт. р-значение 0,7815
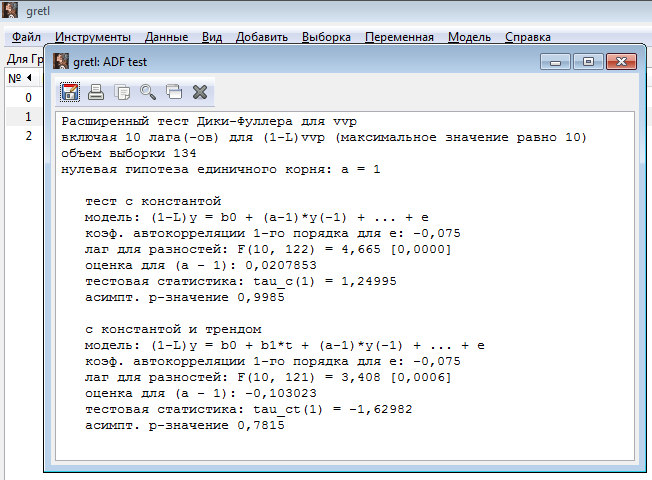
Делаем вывод: ряд ВВП нестационарен, так как tфакт правее tтабл.
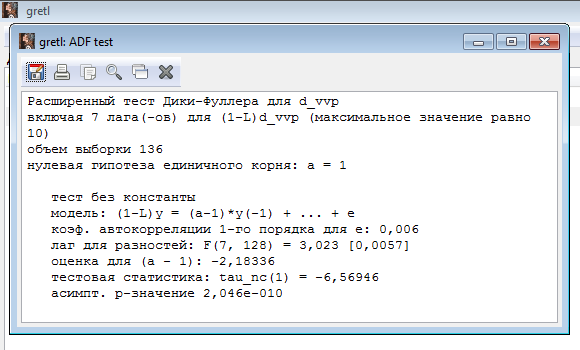
Расширенный тест Дики-Фуллера для d_vvp (используя первую разность)
включая 7 лага(-ов) для (1-L)d_vvp (максимальное значение равно 10)
объем выборки 136
нулевая гипотеза единичного корня: a = 1
тест без константы
модель: (1-L)y = (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: 0,006
лаг для разностей: F(7, 128) = 3,023 [0,0057]
оценка для (a - 1): -2,18336
тестовая статистика: tau_nc(1) = -6,56946
асимпт. р-значение 2,046e-010
тест с константой
модель: (1-L)y = b0 + (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: 0,179
лаг для разностей: F(10, 121) = 5,407 [0,0000]
оценка для (a - 1): -4,7739
тестовая статистика: tau_c(1) = -7,98022
асимпт. р-значение 5,712e-013
с константой и трендом
модель: (1-L)y = b0 + b1*t + (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: 0,196
лаг для разностей: F(10, 120) = 6,655 [0,0000]
оценка для (a - 1): -5,4795
тестовая статистика: tau_ct(1) = -8,80114
асимпт. р-значение 3,262e-015

Делаем вывод: ряд ВВП интегрированный первого порядка, так как так как tфакт левее tтабл.
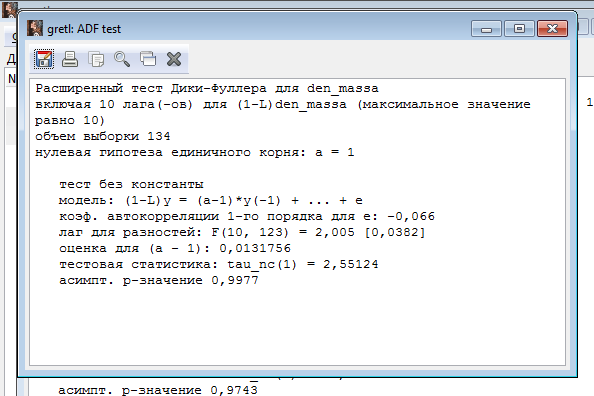
Расширенный тест Дики-Фуллера для den_massa (используя уровень переменной)
включая 10 лага(-ов) для (1-L)den_massa (максимальное значение равно 10)
объем выборки 134
нулевая гипотеза единичного корня: a = 1
тест без константы
модель: (1-L)y = (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: -0,066
лаг для разностей: F(10, 123) = 2,005 [0,0382]
оценка для (a - 1): 0,0131756
тестовая статистика: tau_nc(1) = 2,55124
асимпт. р-значение 0,9977
тест с константой
модель: (1-L)y = b0 + (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: -0,068
лаг для разностей: F(10, 122) = 1,958 [0,0437]
оценка для (a - 1): 0,011262
тестовая статистика: tau_c(1) = 1,82452
асимпт. р-значение 0,9998
с константой и трендом
модель: (1-L)y = b0 + b1*t + (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: 0,007
лаг для разностей: F(6, 129) = 2,758 [0,0148]
оценка для (a - 1): -0,011528
тестовая статистика: tau_ct(1) = -0,670616
асимпт. р-значение 0,9743
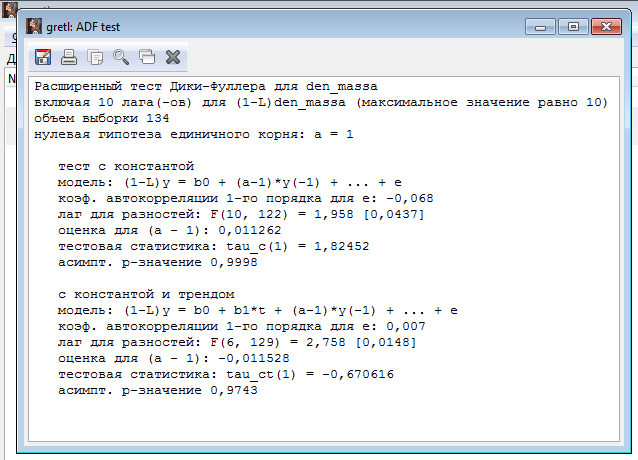
Делаем вывод: ряд Объем денежной массы нестационарен, так как tфакт правее tтабл.
Расширенный тест Дики-Фуллера для d_den_massa (используя первую разность)
включая 10 лага(-ов) для (1-L)d_den_massa (максимальное значение равно 10)
объем выборки 133
нулевая гипотеза единичного корня: a = 1
тест без константы
модель: (1-L)y = (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: 0,224
лаг для разностей: F(10, 122) = 5,582 [0,0000]
оценка для (a - 1): -0,259433
тестовая статистика: tau_nc(1) = -1,73428
асимпт. р-значение 0,07865
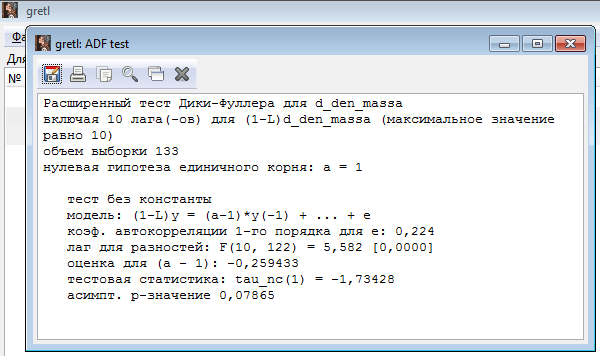
тест с константой
модель: (1-L)y = b0 + (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: 0,247
лаг для разностей: F(10, 121) = 4,264 [0,0000]
оценка для (a - 1): -0,610502
тестовая статистика: tau_c(1) = -3,03843
асимпт. р-значение 0,03148
с константой и трендом
модель: (1-L)y = b0 + b1*t + (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: 0,262
лаг для разностей: F(10, 120) = 4,090 [0,0001]
оценка для (a - 1): -0,958474
тестовая статистика: tau_ct(1) = -4,17219
асимпт. р-значение 0,004859
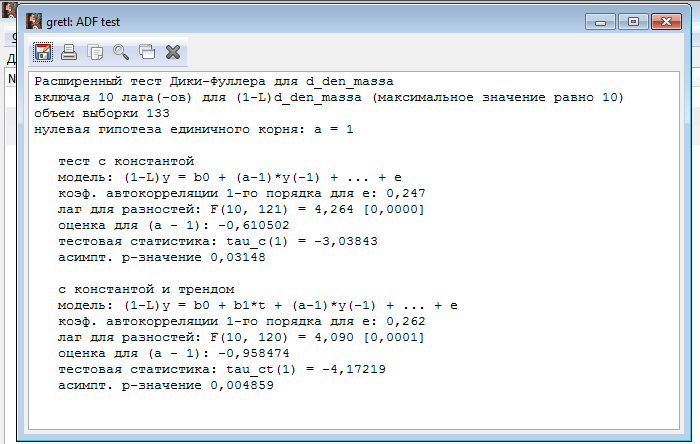
Делаем вывод: ряд Объем денежной массы интегрированный первого порядка, так как tфакт левее tтабл.
Выбор наилучшей модели по информационным критериям
Для ΔYt
Переменная тест единичного корня Расширенный тест Дики-Фуллера.
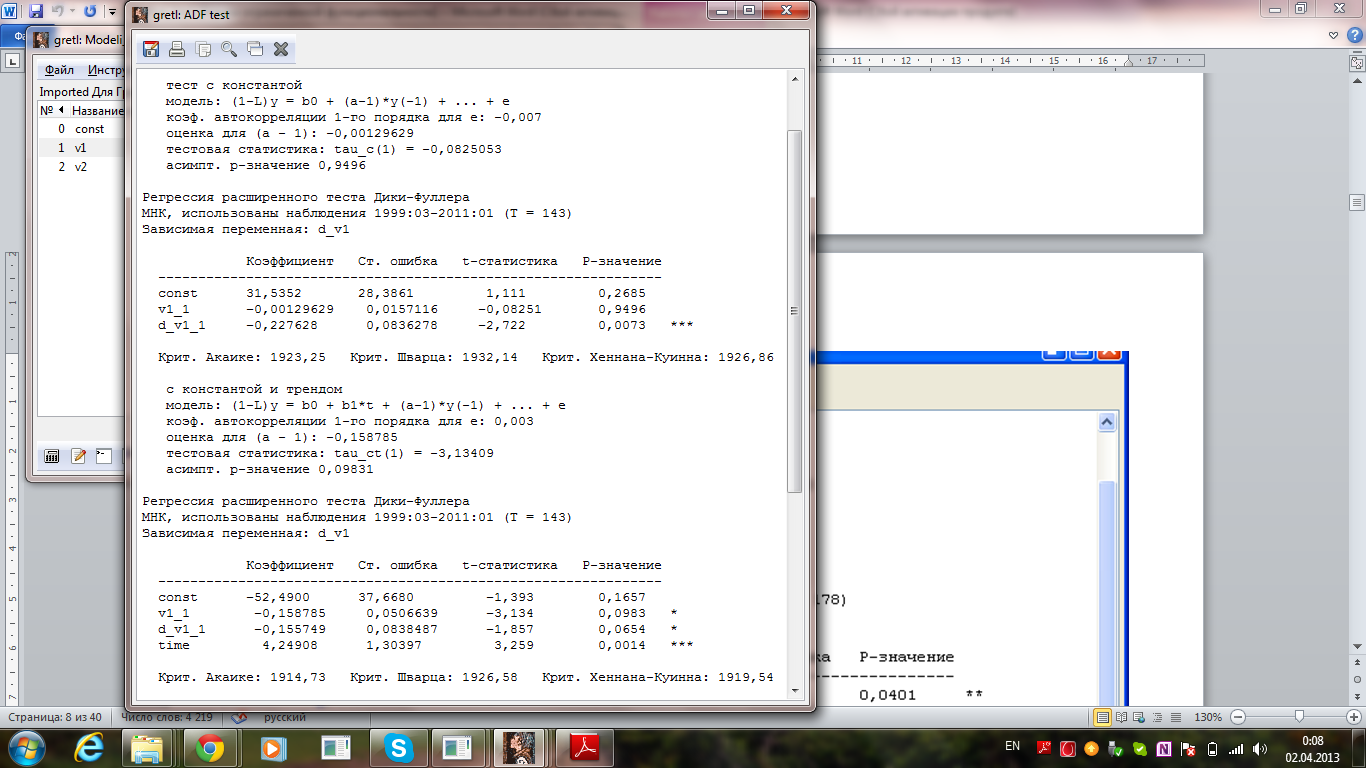
Рассмотрев все лаги до порядка 13, было вычислено, что наилучшая модель имеет лаг 1 (ADF(1)), при этом модель содержит константу.
Данная модель имеет наилучшие значения по критериям:
Критерий Акаике: 1923,25;
Крит. Шварца: 1932,14;
Крит. Хеннана-Куинна: 1926,86.
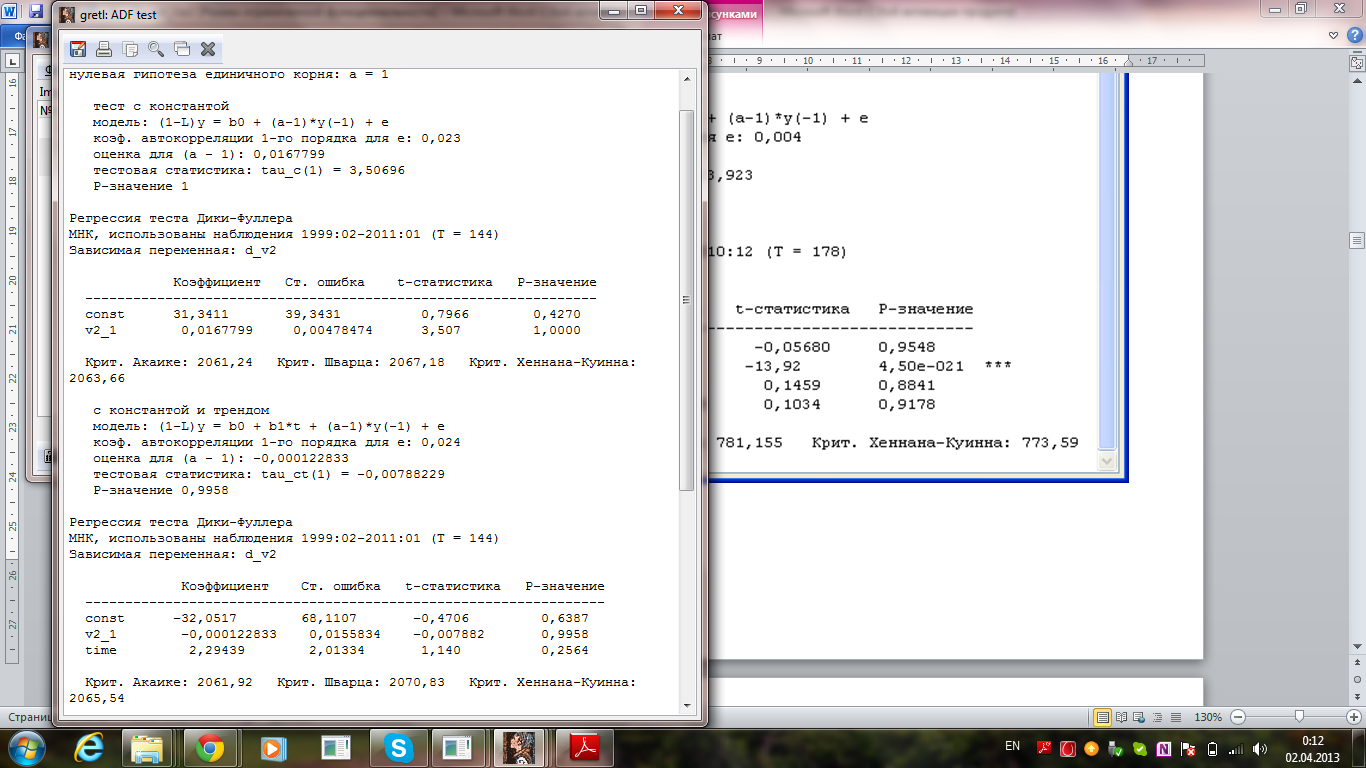
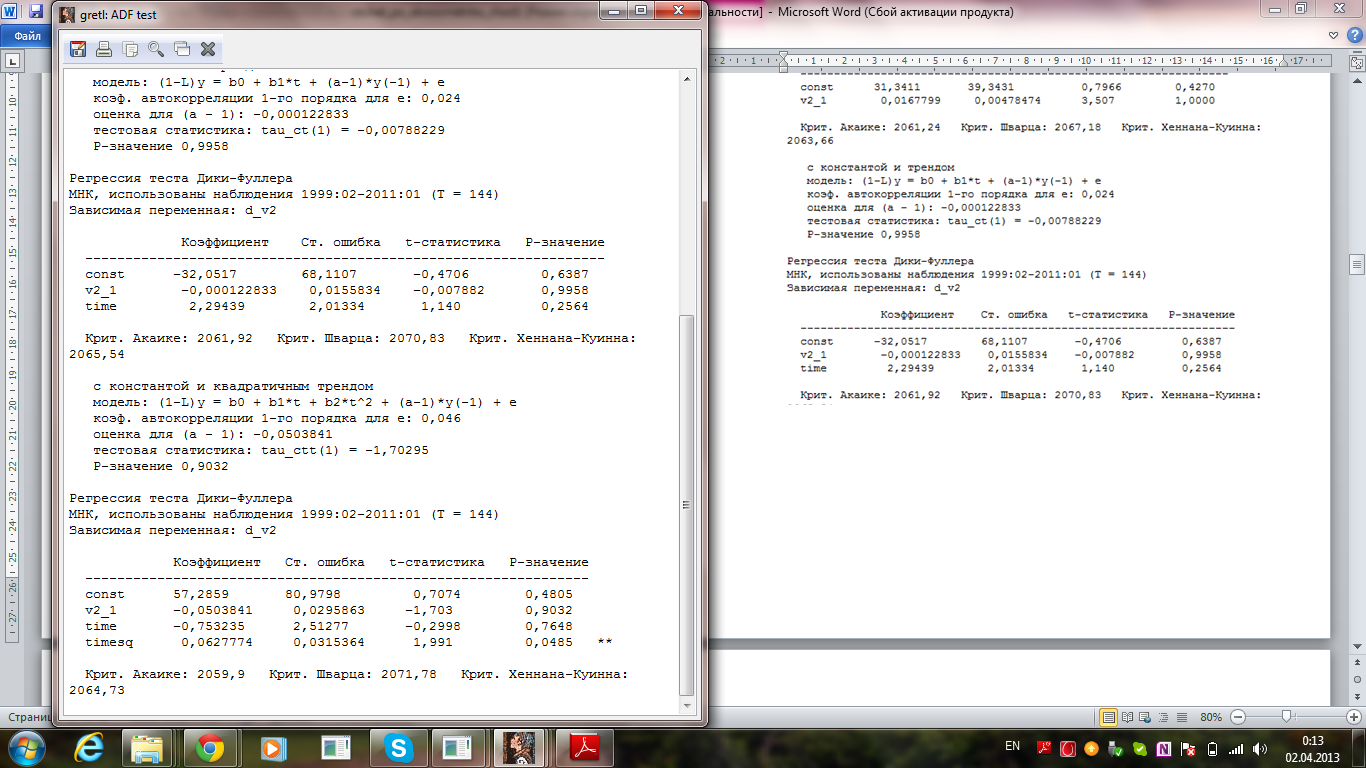
Для ΔXt
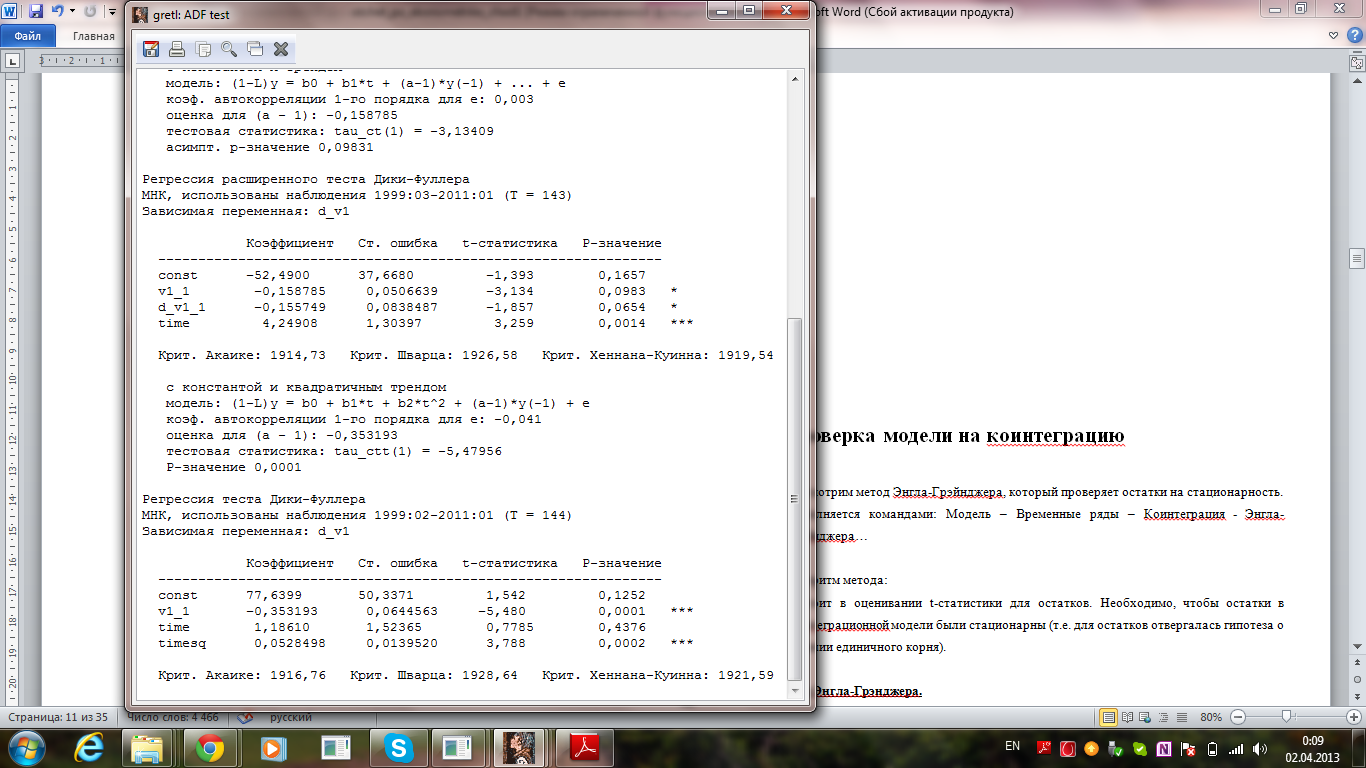
Рассмотрев все лаги до порядка 13, было вычислено, что наилучшая модель имеет лаг 1 (ADF(1)), при этом модель содержит константу и тренд.
Данная модель имеет наилучшие значения по критериям:
Критерий Акаике: 2061,92;
Критерий Шварца: 2070,83;
Критерий Хеннана-Куинна: 2070,83.
Проверка модели на коинтеграцию
Рассмотрим метод Энгла-Грэйнджера, который проверяет остатки на стационарность.
Выполняется командами: Модель – Временные ряды – Коинтеграция - Энгла-Грэйнджера…
Алгоритм метода:
Состоит в оценивании t-статистики для остатков. Необходимо, чтобы остатки в коинтеграционной модели были стационарны (т.е. для остатков отвергалась гипотеза о наличии единичного корня).
Тест Энгла-Грэнджера.
Коинтеграционная регрессия -
МНК, использованы наблюдения 1999:01-2011:01 (T = 145)
Зависимая переменная: vvp
Коэффициент Ст. ошибка t-статистика P-значение
-----------------------------------------------------------------
const 281,407 40,3595 6,973 1,06e-010 ***
den_massa 0,189672 0,00482708 39,29 1,63e-078 ***
Среднее зав. перемен 1480,428 Ст. откл. зав. перемен 1088,689
Сумма кв. остатков 14467712 Ст. ошибка модели 318,0767
R-квадрат 0,915232 Испр. R-квадрат 0,914640
Лог. правдоподобие -1040,272 Крит. Акаике 2084,543
Крит. Шварца 2090,497 Крит. Хеннана-Куинна 2086,962
Параметр rho 0,797935 Стат. Дарбина-Вотсона 0,407521
Тестирование единичного корня для uhat
Расширенный тест Дики-Фуллера для uhat
включая 12 лага(-ов) для (1-L)uhat
объем выборки 132
нулевая гипотеза единичного корня: a = 1
модель: (1-L)y = (a-1)*y(-1) + ... + e
коэф. автокорреляции 1-го порядка для e: -0,142
лаг для разностей: F(12, 119) = 9,106 [0,0000]
оценка для (a - 1): -0,338233
тестовая статистика: tau_c(2) = -4,72963
асимпт. р-значение 0,0004688
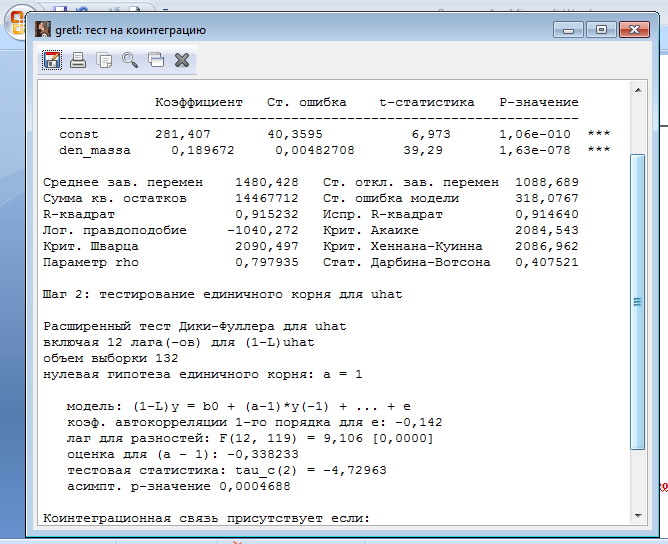
Ряды являются коинтегрированными, т.к. выполняются необходимые условия.
А именно:
Проверка гипотезы единичного корня для отдельных переменных была проведена ранее. Для отдельных переменных гипотеза не была отвергнута, так, они оказались интегрированными первого порядка.
Гипотеза единичного корня отвергается для остатков (uhat) комнтеграционной регрессии, т.е. ряд uhat стационарен, так как tфакт левее tтабл.
Построение VAR модели
Фактически VAR - это система
эконометрических уравнений, каждая из
которых представляет собой модель
авторегрессии и распределенного лага
(ADL). Пусть
![]() - i-й временной ряд.
ADL(p,p)-модель
для i-го временного ряда
будет иметь вид
- i-й временной ряд.
ADL(p,p)-модель
для i-го временного ряда
будет иметь вид
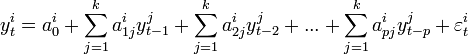
С помощью функции «выбор порядка лагов для VAR» подбираем максимальный лаг для уравнения, для этого выбираем Модель->Временные ряды->Выбор порядка лагов для VAR… В появившемся диалоговом окне заносим в окно «Эндогенные переменные» исследуемые переменные, выбираем флажок «Включить константу». Получили результат:
VAR система, максимально возможный порядок лага равен 24
Звездочка указывает на наилучшие (минимальные) значения информационных критериев Акаике (AIC), Шварца (BIC) и Хеннана-Куинна (HQC).
lags loglik p(LR) AIC BIC HQC
1 -1690,72383 28,045022 28,183656 28,101327
2 -1686,63855 0,08553 28,043612 28,274669 28,137453
3 -1682,89127 0,11195 28,047790 28,371270 28,179167
4 -1668,62451 0,00001 27,878091 28,293994 28,047005
5 -1649,14574 0,00000 27,622244 28,130569 27,828694
6 -1645,42862 0,11464 27,626919 28,227668 27,870906
7 -1628,99857 0,00000 27,421464 28,114635 27,702987
8 -1626,86376 0,37074 27,452294 28,237888 27,771353
9 -1579,87533 0,00000 26,741741 27,619758 27,098337
10 -1567,23163 0,00004 26,598870 27,569310 26,993002
11 -1563,73055 0,13577 26,607117 27,669979 27,038786
12 -1543,30211 0,00000 26,335572 27,490857 26,804778
13 -1523,52644 0,00000 26,074817 27,322525* 26,581559
14 -1519,84408 0,11782 26,080067 27,420198 26,624346
15 -1511,87293 0,00310 26,014429 27,446982 26,596243
16 -1504,27286 0,00430 25,954923 27,479900 26,574274
17 -1491,40970 0,00004 25,808425 27,425824 26,465312*
18 -1488,96639 0,29913 25,834155 27,543978 26,528579
19 -1484,19327 0,04881 25,821376 27,623621 26,553337
20 -1480,79295 0,14681 25,831288 27,725956 26,600785
21 -1479,04216 0,47764 25,868466 27,855556 26,675499
22 -1476,57152 0,29337 25,893744 27,973258 26,738314
23 -1466,28386 0,00038 25,789816 27,961752 26,671922
24 -1460,81523 0,02728 25,765541* 28,029900 26,685184
Таким образом, выбирая из максимальных лагов 13, 17 и 24(выделены цветом в таблице), так как на них указывают наилучшие значения по критериям Шварца и Хеннана-Куинна, мы приняли решения остановиться на лаге 17. Это связано с тем, что в сравнении с другими, у него самые минимальные значения по критериям.
Построим модель VAR для лага 17 и выбираем значимые коэффициенты в модели. Для этого выбираем пункты меню Модель->Временные ряды->Векторная авторегрессия(VAR)
…. В появившемся диалоговом окне заносим в окно «Эндогенные переменные» исследуемые переменные, выбираем флажок «Включить константу». Вводим максимальный порядок лага 17. При построении получили следующий результат:
