
- •Лекция №4. Характеристики типовых звеньев сар
- •4.1. Общие положения
- •4.2. Безынерционное звено
- •4.3. Апериодическое звено 1-го порядка
- •4.4. Апериодическое звено 2-го порядка
- •4.5. Идеальное интегрирующее звено
- •4.6. Инерционное интегрирующее звено
- •4.7. Идеальное дифференцирующее звено
- •4.8. Реальное дифференцирующее звено
- •4.9. Неустойчивые звенья
4.9. Неустойчивые звенья
Рассмотренные выше звенья позиционного типа относятся к устойчивым звеньям или звеньям с самовыравниванием. Под самовыравниванием понимается способность звена самопроизвольно приходить к новому установившемуся режиму при ограниченном изменении входной величины или возмущающего воздействия. Термин «самовыравнивание» обычно применяется для звеньев, представляющих собой объекты регулирования.
Существуют звенья, у которых ограниченное изменение входной величины или возмущающего воздействия не вызывает прихода звена к новому установившемуся состоянию, а выходная величина имеет тенденцию неограниченного возрастания во времени. К таким звеньям относятся, например звенья интегрирующего типа. Они были рассмотрены выше.
Существуют звенья, у которых этот процесс выражен еще заметнее. Это объясняется наличием положительных вещественных корней или комплексных корней с положительной вещественной частью в характеристическом уравнении (в знаменателе передаточной функции, приравненном нулю), в результате чего звено относится к категории неустойчивых звеньев.
(Слайд 46)
Рассмотрим в качестве примера звено, описываемое дифференциальным уравнением вида
![]() (4.55)
(4.55)
или
![]() . (4.56)
. (4.56)
Этому дифференциальному уравнению соответствует передаточная функция
![]() . (4.57)
. (4.57)
(Слайд 47)
П
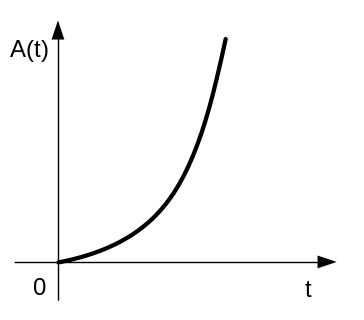 Рис. 4.25.
Переходная функция неустойчивого звена
Рис. 4.25.
Переходная функция неустойчивого звена
![]() . (4.58)
. (4.58)
Эта характеристика изображена на рис. 4.25.
Таким звеном может быть, например, асинхронный двухфазный управляемый двигатель, если он имеет механическую характеристику с отрицательным наклоном.
Существенной особенностью неустойчивых звеньев является наличие больших по сравнению с устойчивыми звеньями фазовых сдвигов.
(Слайд 48)
Так, для рассмотренного выше апериодического звена с отрицательным самовыравниванием имеем частотную передаточную функцию
![]() . (4.59)
. (4.59)
Модуль её не отличается от модуля частотной передаточной функции апериодического звена с положительным самовыравниванием (4.8)
![]() , (4.60)
, (4.60)
а фаза
![]() (4.61)
(4.61)
имеет большое значение по сравнению со вторым уравнением в (4.8).
В связи с этим неустойчивые звенья относят к группе так называемых неминимально-фазовых звеньев. К неминимально-фазовым звеньям относятся также устойчивые звенья, имеющие в числителе передаточной функции (в правой части дифференциального уравнения) вещественные положительные корни или комплексные корни с положительной вещественной частью.
(Слайд 49)
Например, звено с передаточной функцией
![]() (4.62)
(4.62)
относится к группе неминимально-фазовых звеньев.
(Слайд 50)
К неустойчивым звеньям относится также ряд других звеньев, имеющих передаточные функции вида
![]() ; (4.63)
; (4.63)
![]() ; (4.64)
; (4.64)
![]() ; (4.65)
; (4.65)
![]() . (4.66)
. (4.66)
Наличие в автоматической системе неустойчивых звеньев вызывает некоторые особенности расчета.
