4.7. Идеальное дифференцирующее звено

(Слайд 33)

Звено описывается уравнением

(4.42)

или в операторной форме

. (4.43)

Передаточная функция

. (4.44)

(Слайд 34)

Примеры идеальных дифференцирующих звеньев изображены на рис. 4.17. Единственным идеальным дифференцирующим звеном, которое точно описывается уравнением (4.42), является тахогенератор постоянного тока (рис. 4.17, а), если в качестве входной величины рассматривать угол поворота его ротора , а в качестве выходной – напряжение якоря U. Приближенно в качестве идеального дифференцирующего звена может рассматриваться операционный усилитель в режиме дифференцирования (рис. 4.17, б).

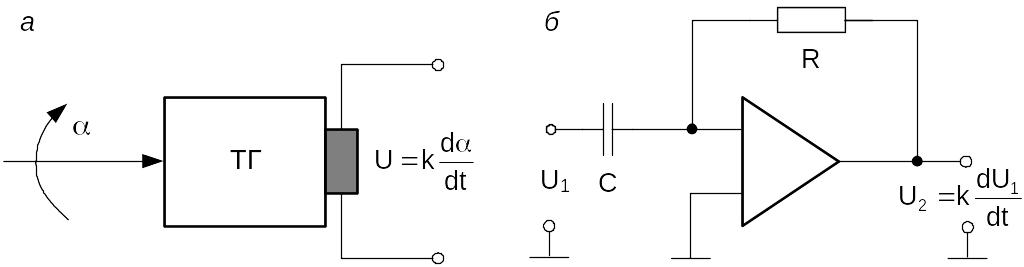
Рис. 4.17. Идеальные дифференцирующие звенья

(Слайд 35)

П

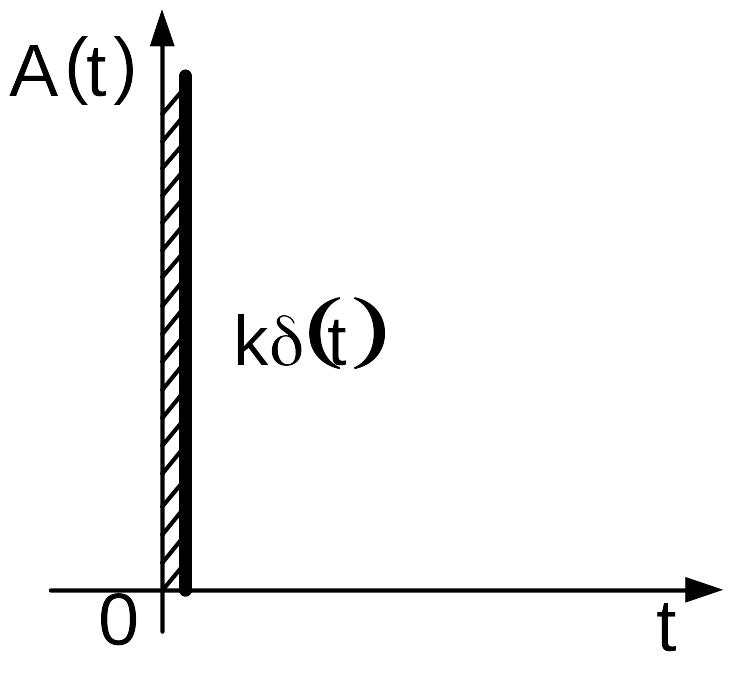
Рис. 4.18. Переходная функция идеального дифференцирующего звена

ереходная функция звена при х₁ = 1(t); A(t) = k 1’(t) = k (t) представляет собой импульсную функцию, площадь которой равна k (рис. 4.18). Функция веса представляет собой импульсную функцию второго порядка.

(Слайд 36)

Частотная передаточная функция, её модуль и фаза соответственно равны

w(j) = k j; (4.45)

A() = k;  = + 90 при  > 0;  = - 90 при  < 0. (4.46)

(Слайд 37)

Частотные характеристики изображены на рис. 4.19.

Из амплитудной характеристики видно, что звено пропускает сигнал тем сильнее, чем выше его частота. Это свойство является в автоматических системах часто нежелательным, так как звено может в значительной степени повышать уровень действующих в системе помех, которые, как правило, являются высокочастотными.

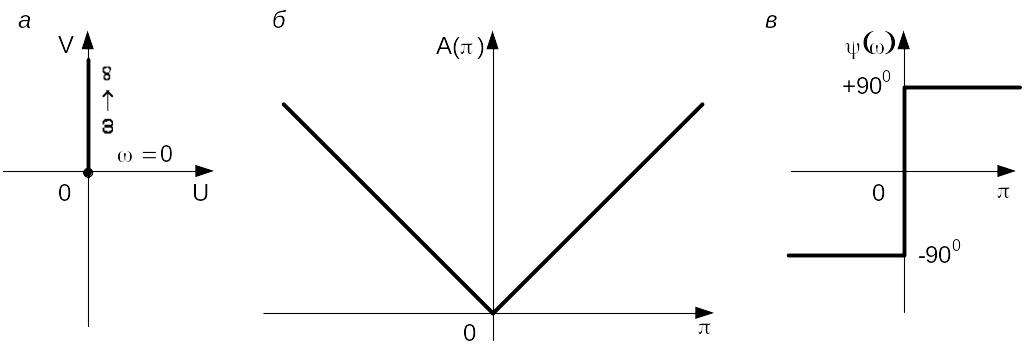
Рис. 4.19. АФЧХ (а), АЧХ (б) и ФЧХ (в) идеального дифференцирующего звена

Амплитудно-фазовая характеристика для положительных частот сливается с положительным направлением оси мнимых.

ЛАХ строится по выражению

. (4.47)

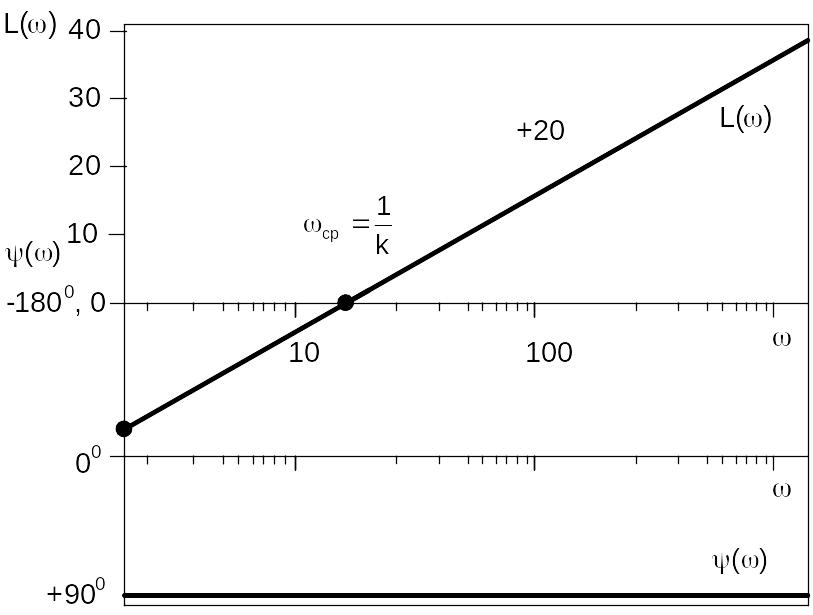
Рис. 4.20. ЛАХ и ЛФХ идеального дифференцирующего звена

(Слайд 38)

Нетрудно видеть, что ЛАХ представляет собой прямую с положительным наклоном 20 дБ/дек (рис. 4.20). Эта прямая пересекает ось нуля децибел при частоте среза .

ЛФХ представляет собой прямую линию  = + 90, параллельную оси частот.

4.8. Реальное дифференцирующее звено

(Слайд 39)

Звено описывается уравнением

. (4.48)

Передаточная функция звена

. (4.49)

Звено условно можно представить в виде двух включенных последовательно звеньев – идеального дифференцирующего звена и апериодического звена первого порядка.

(Слайд 40)

На рис. 4.21 изображены примеры реальных дифференцирующих звеньев: дифференцирующая RC-цепь (рис. 4.21, а), RL-цепь (рис. 4.21, б) и дифференцирующий трансформатор (рис. 4.21, в).

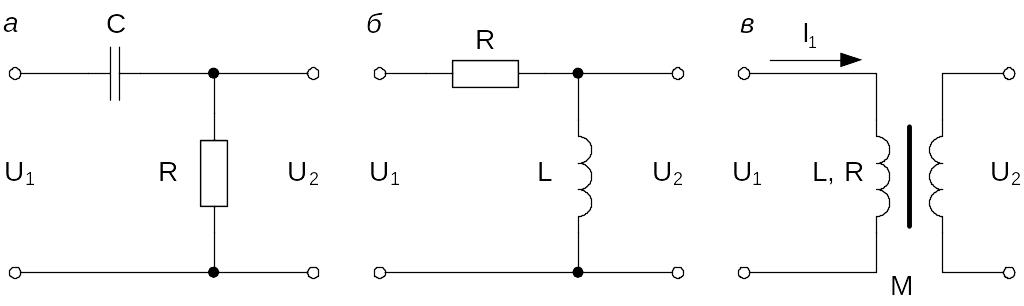
Рис. 4.21. Реальные дифференцирующие звенья

(Слайд 41)

Переходная функция определяется решением (4.48) при х₁ = 1(t) и нулевых начальных условиях

. (4.50)

Функция веса

. (4.51)

(Слайд 42)

Временные характеристики изображены на рис. 4.22. Там же показаны построения, позволяющие по экспериментальным характеристикам определять параметры звена.

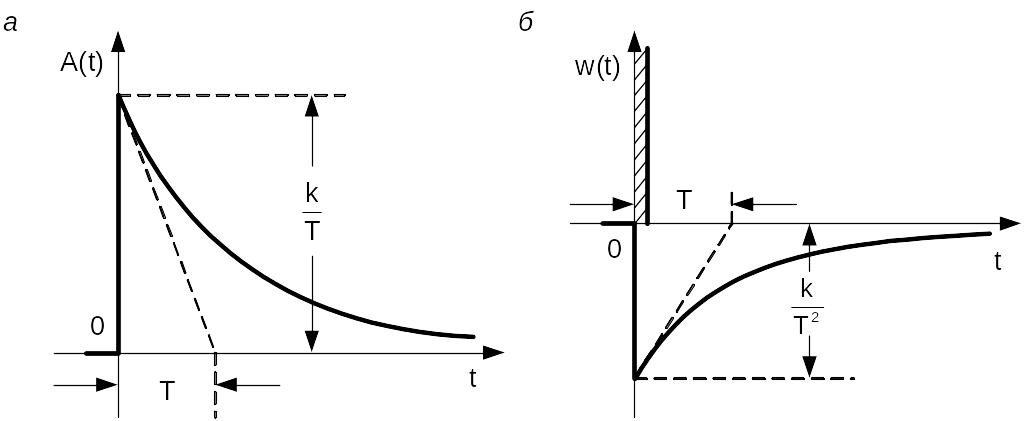
Рис. 4.22. Переходная функция (а) и дельта-функция (б) реального дифференцирующего звена

(Слайд 43)

Частотная передаточная функция, её модуль и фаза соответственно равны:

; (4.52)

(4.53)

(Слайд 44)

Амплитудная, фазовая и амплитудно-фазовая характеристики звена изображены на рис. 4.23.

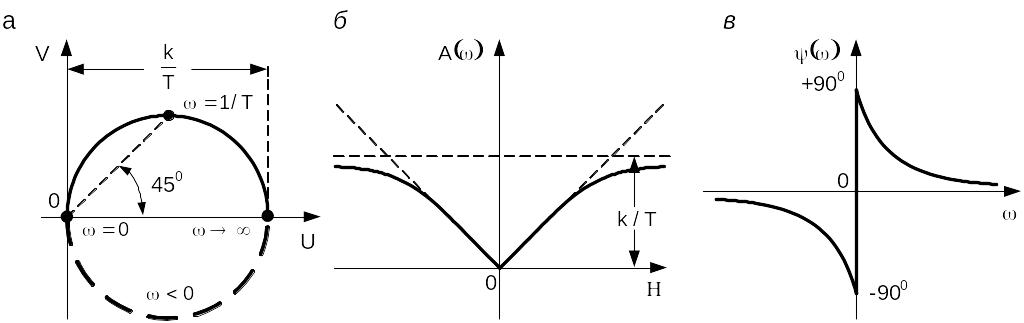
Рис. 4.23. АФЧХ (а), АЧХ (б) и ФЧХ (в) реального дифференцирующего звена

Амплитудная характеристика реального звена отличается от амплитудной характеристики идеального дифференцирующего звена (показана пунктиром). Характеристики совпадают в области низких частот. В области высоких частот реальное звено пропускает сигнал хуже, чем идеальное звено. Коэффициент передачи стремится к значению k / T при . Для звеньев, представляющих собой RC- или RL-цепь (см. рис. 4.21), коэффициент k / T = 1, и на высоких частотах коэффициент передачи стремится к единице.

Это означает, что в дифференцирующей RC-цепи конденсатор имеет сопротивление, стремящееся к нулю, а в дифференцирующей RL-цепи индуктивность имеет сопротивление, стремящееся к бесконечности. И в том, и в другом случаях напряжение на выходе будет равно напряжению на входе.

Фазовые сдвиги, вносимые звеном, являются наибольшими при низких частотах. На высоких частотах фазовый сдвиг постепенно уменьшается, стремясь в пределе к нулю при . Здесь также видно, что реальное звено ведет себя подобно идеальному только в области низких частот.

Амплитудно-фазовая характеристика для положительных частот представляет собой полуокружность с диаметром, равным k / T. На полуокружности нанесены характерные точки: и . Дополнив эту полуокружность её зеркальным изображением относительно вещественной оси, получим полную амплитудно-фазовую характеристику для всех частот, лежащих в пределах .

ЛАХ строится по выражению

. (4.54)

(Слайд 45)

Для построения асимптотической ЛАХ (рис. 4.24) проведем вертикальную линию при сопрягающей частоте .

Левее этой линии, то есть при , можно воспользоваться приближенным выражением . Этому выражению соответствует прямая линия с положительным наклоном 20 дБ/дек (прямая а–b). Она может быть построена, например, по частоте среза .

Для частот можно пользоваться приближенным выражением . Этому выражению соответствует прямая, параллельная оси частот (b – с). Действительная ЛАХ отличается от асимптотической в точке излома b на величину 3 дБ.

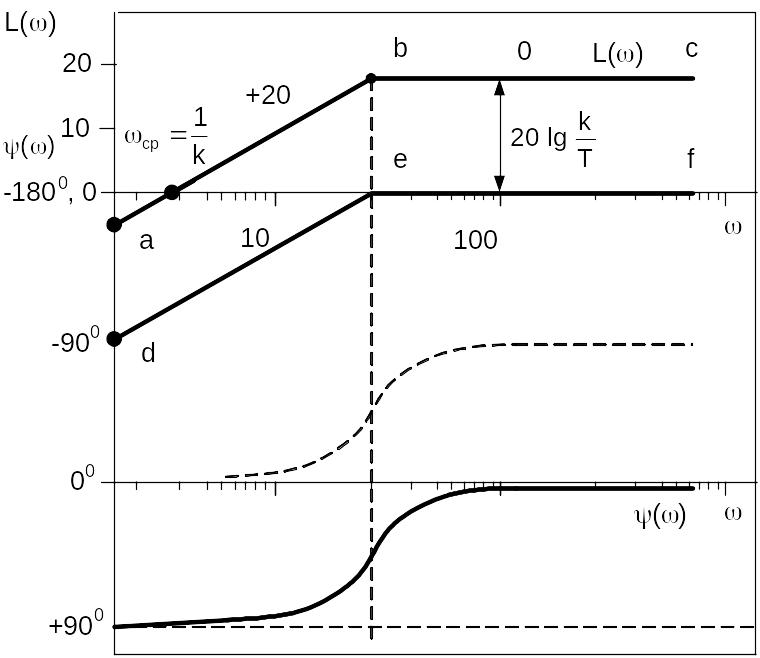
Рис. 4.24. ЛАХ и ЛФХ реального дифференцирующего звена

На рис. 4.24 показана асимптотическая ЛАХ для случая k = 1 (ломаная прямая d–e–f).

ЛФХ строится по второму уравнению системы (4.53). Для этого сначала строится первое слагаемое ₁ = + 90, а затем второе ₂ = –аrctg Т. Результирующая ЛФХ показана сплошной линией. При фазовый сдвиг равен + 45.