1.4.2. Программа для системы Mathcad.
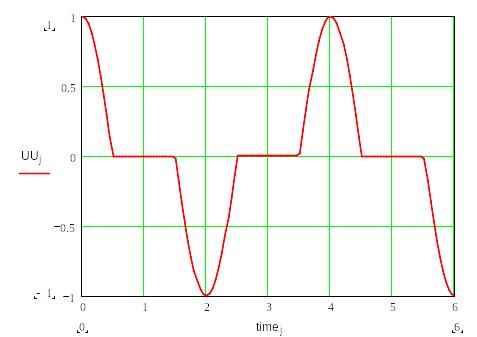
1.5. Варианты заданий.
Методом конечных разностей решить следующие краевые задачи. Построить график изменения функции со временем в средней точке области. Полученный результат сравнить с аналитическим решением.
-
Решить уравнение
с начальными условиями
;
№
g(x,t)
(x)
(x)
Левое ГУ
Правое ГУ
Решение
u(x,t)
1.
0
2.
0
3.
0
4.
0
5.
6.
0
0
7.
0
0
8.
0
0
Решить уравнение
с начальными условиями
;
№
g(x,t)
(x)
(x)
Левое ГУ
Правое ГУ
Решение
u(x,t)
9.
0
10.
0
11.
0
12.
0
13.
14.
1
15.
16.
1
1
Решить уравнение
с начальными условиями
;
№
g(r,t)
(r)
(r)
Левое ГУ
Правое ГУ
Решение
u(r,t)
17.
0
18.
19.
0
20.
