2. Разностная схема для решения уравнения гиперболического типа.

2.1. Построение разностной схемы.

Требуется найти решение гиперболического уравнения

, (2.1)

на отрезке [a, b] в течение промежутка времени при следующих начальных и краевых условиях.

Известно, что в начальный момент времени t=0 задано распределение функции и известна скорость изменения функции , а на границах отрезка задано одно из условий:

	x=a	x=b
1)
2)
3)

Требуется найти решение на отрезке в течение промежутка времени .

Как видно из уравнения (2.1), его решение зависит от двух переменных t – времени и x – пространства. Выбор системы координат и построение разностной сетки сделаем так же, как и в п.1.1.

Запишем конечно-разностную схему для уравнения (2.1), используя для производных по времени и пространству следующий шаблон (рис.5).

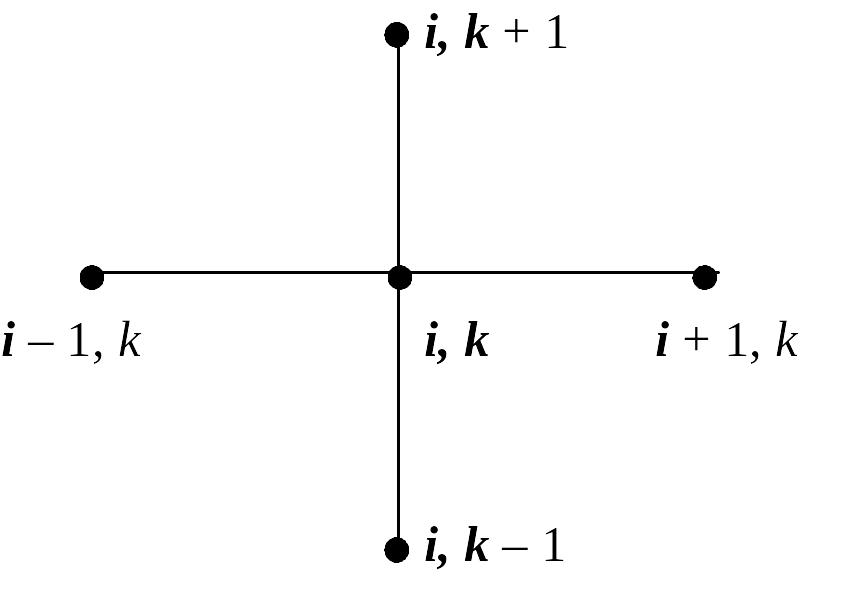
Рис.5.

Разностные аналоги имеют следующий вид:

; ;

Известную функцию f(x,t) в момент времени t_k и в точке пространства x_k обозначим как .

Тогда разностная схема для уравнения (2.1) запишется в виде:

(2.2)

В этом уравнении искомой величиной является значение функции в точке x_i в момент времени t_k+1.

Введем число Куранта и перепишем уравнение (2.2) в виде:

(2.3)

Как видно из уравнения (2.3) для нахождения значения функции в узле i на k + 1-ом временном слое, необходимо знать значения функции в трех узлах (i – 1, i, i + 1) на k-ом временном слое и одно значение в узле i на k – 1-ом временном слое.

Полученная явная разностная схема (2.3) обладает первым порядком аппроксимации по времени и вторым порядком по пространству . Условие устойчивости разностной схемы: r 1.

2.2. Реализация начальных и граничных условий.

Начальные условия.

При использовании разностной схемы для нахождения значений функции на временном слое с номером 1, требуются значения функций с фиктивного слоя k = – 1, на котором они не определены. В этом случае поступают следующим образом.

Заменим в начальном условии , производную по времени u_t разностным аналогом с первым порядком точности

. (2.4)

Исключая из (2.4) и (2.3), записанного для k=0, величину , получим уравнение для нахождения значения функции на первом временном слое:

(2.5)

Значения функции на нулевом временном слое известны из начальных условий:

.

Граничные условия.

Реализация граничных условий первого рода не составляет труда:

; (2.6)

При реализации граничных условий второго рода производные в точке и в точке заменяют конечно-разностным аналогом со вторым порядком точности:

; .

Выражая отсюда , и подставляя в уравнения (2.3) и (2.5), записанных, соответственно, для i=0 и i=N получим следующие уравнения для нахождения значения функции в крайней левой и крайней правой точках области:

на первом временном слое

; (2.7)

; (2.8)

на последующих временных слоях ( )

; (2.9)

. (2.10)

При реализации граничных условий третьего рода их разностные аналоги принимают вид:

; .

Тогда из уравнения (2.3) и (2.6) получаем

на первом временном слое

; (2.11)

; (2.12)

на последующих временных слоях ( )

; (2.13)

. (2.14)

Для граничных условий третьего рода условие устойчивости имеет вид:

.