
Лабораторная работа №5
Тема: Кредит и расчет выплат по кредиту
Цель:
Научить использовать возможности финансовых расчетов электронных таблиц;
Упростить расчеты выгодности кредитов в реальной экономической действительности;
Условие задачи:
Банк А предлагает кредит в 5 тыс. у.е. на 18 месяцев под 13% годовых. Выплаты кредита – ежемесячно равными частями (аннуитет). Банк Б предлагает аналогичные условия, но с дифференцированными выплатами (размер ежемесячного платежа по мере погашения долга уменьшается). Дополнительных комиссий в обоих случаях не предусмотрено.
Сколько заёмщик заплатит за кредит банку А и банку Б?
Каков будет размер его ежемесячных выплат?
В каком банке ему выгоднее взять кредит?
Основные понятия и формулы, необходимые для решения задачи:
Аннуитет – выплата кредита ежемесячно равными частями.
Пошаговое решение задачи:
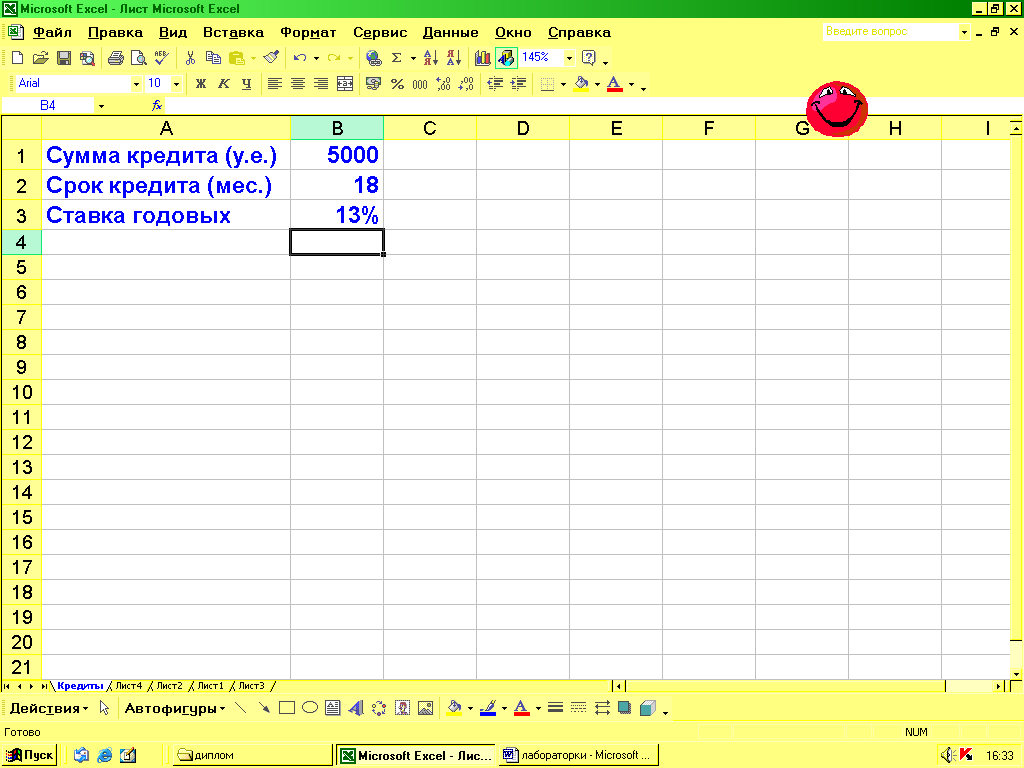
Рассчитаем размер его ежемесячных выплат на условиях банка А. Условие задачи запишем в ячейках А1:В3
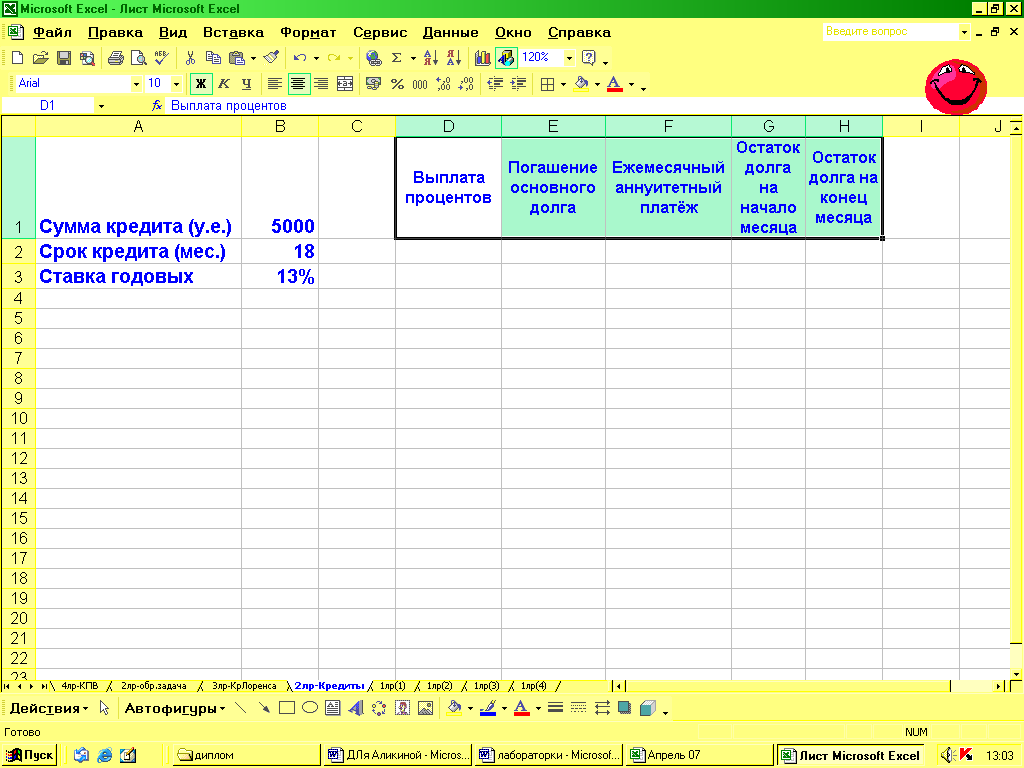
В первой строке обозначим все величины, которые необходимо найти в задаче и вспомогательные расчетные величины («шапки» столбцов): Выплата процентов; Погашение основного долга; Ежемесячный аннуитетный платеж; Остаток долга на начало месяца; Остаток долга на конец месяца.
Вычислим значения ежемесячного аннуитетного платежа. Для этого вызовем функцию ПЛТ (ППЛАТ) из раздела финансовых (Вставка/Функция/Категория/Финансовые). В необходимые поля формулы последовательно вводим условия задачи, а именно обозначения ячеек со значениями переменных. Обратите внимание, что годовая процентная ставка в поле «Норма» делится на 12, потому что срок кредита задан в месяцах.
В результате расчета мы получим отрицательное значение платежа, поскольку программа предполагает, что платеж мы отдаем, а не получаем. Поэтому для удобства в строке формул лучше обозначить знак «-». (‘= -ПЛТ(В3/12;В2;В1)’)
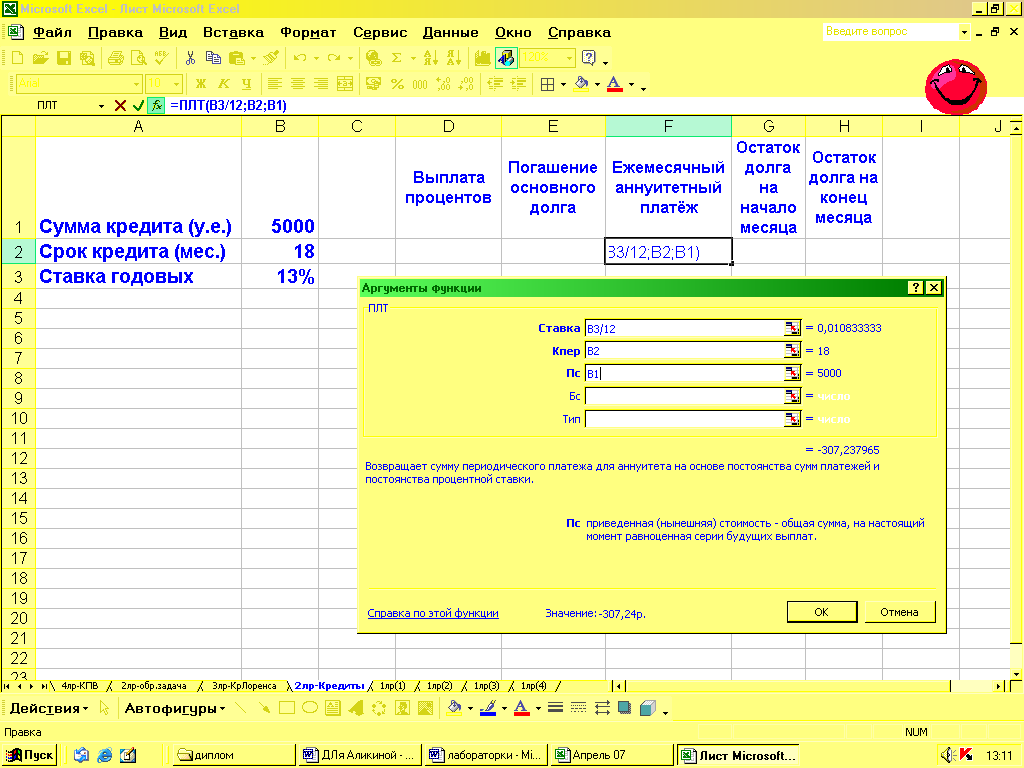
В данном случае мы специально указали адреса ячеек, чтобы при изменении данных расчет остальных показателей производился автоматически. Самостоятельно установите в формулу знаки ‘$’, чтобы исходные данные задачи обрабатывались как константы.
Следующим шагом задаем начальное условие в столбце «Остаток долга на начало месяца». То есть в ячейку G2 копируем начальное значение ‘=B1’.
Далее задаем значение столбца «Выплата процентов», учитывая, что ставка годовая: В ячейку D2 заносим формулу 'G2*$B$3/12'.
Значение в ячейке “Погашение основного долга» есть разница между значением ячейки «Ежемесячный аннуитетный платеж» и значением ячейки «Выплата процентов» (‘=F2-D2’).
И последним задаем значение в столбце «Остаток долга на конец месяца». Это разница между значением ячейки «Остаток долга на начало месяца» и значением ячейки «Погашение основного долга» (‘=G2-E2’).
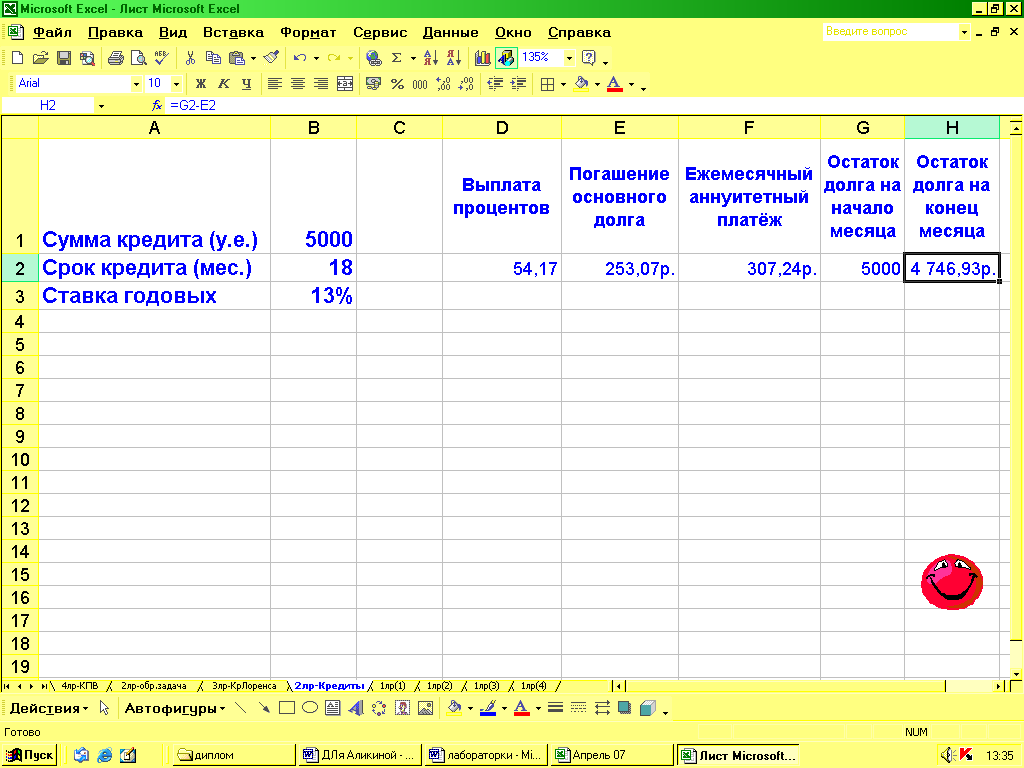
Теперь ячейке G3 присваиваем значение '=H2', а остальные значения строки скопируем в строку 3.
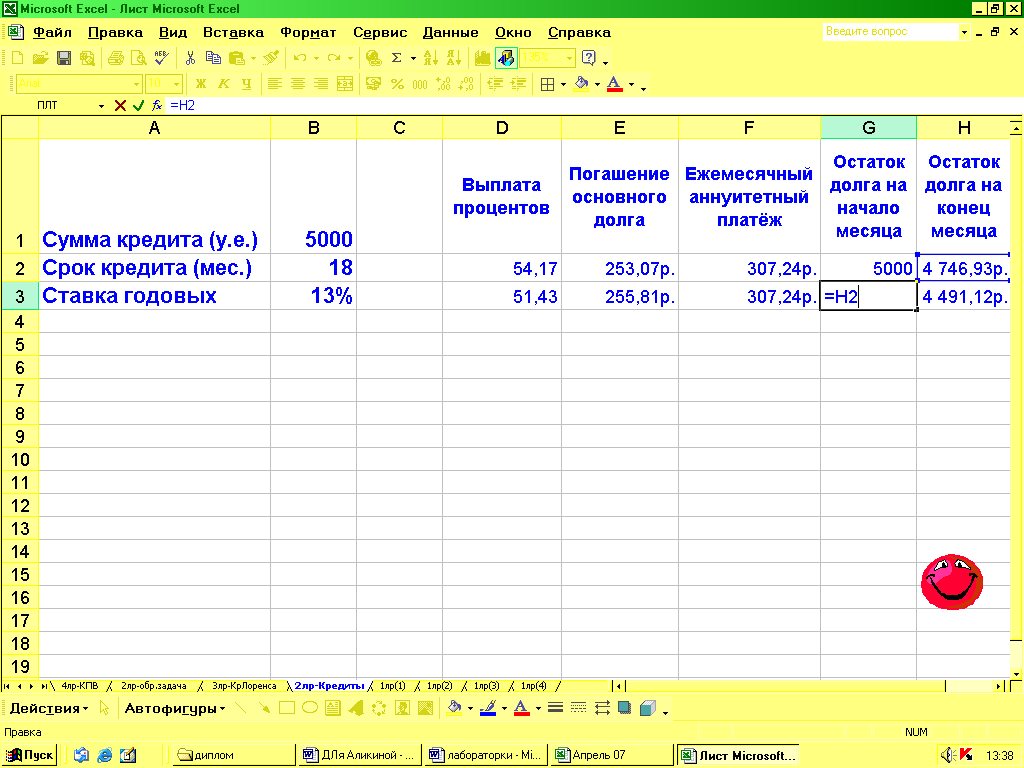
Получившуюся строку копируем таким образом, чтобы количество получившихся строк совпадало со сроком выплаты кредита (18). О верном решении задачи свидетельствует значение, равное нулю в последней строчке столбца «Остаток долга на конец месяца»
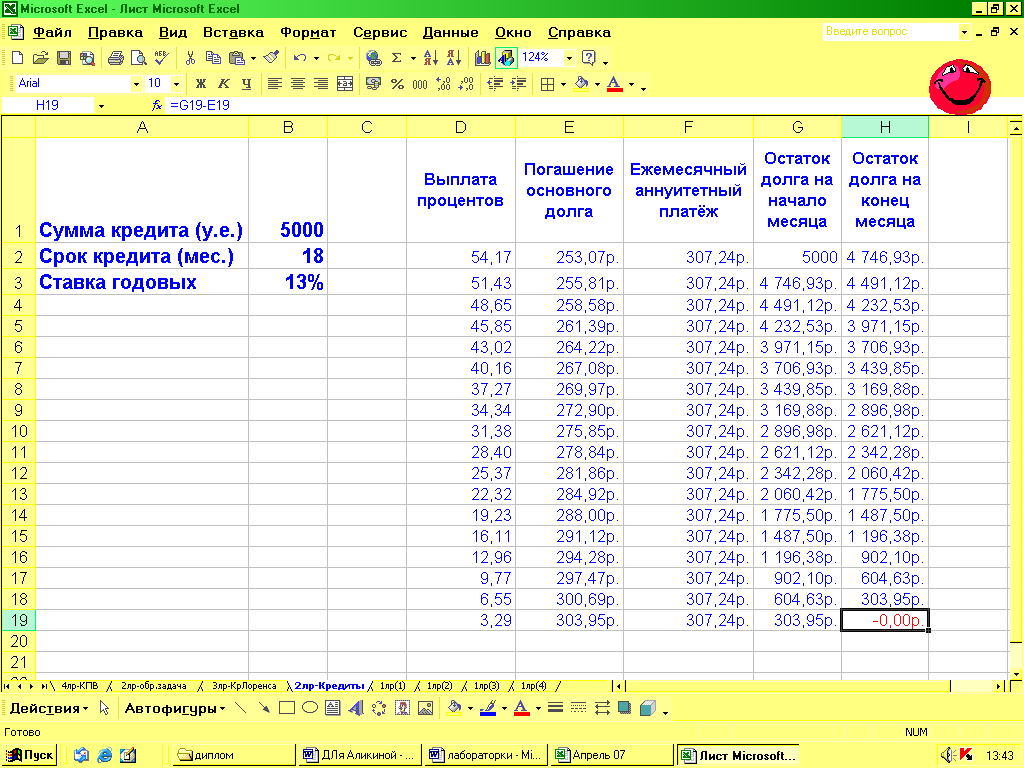
Теперь рассчитаем размеры выплат на условиях банка Б, то есть дифференцированные платежи. Исходные условия те же самые, поэтому скопируем все данные на другой лист и внесем поправки.
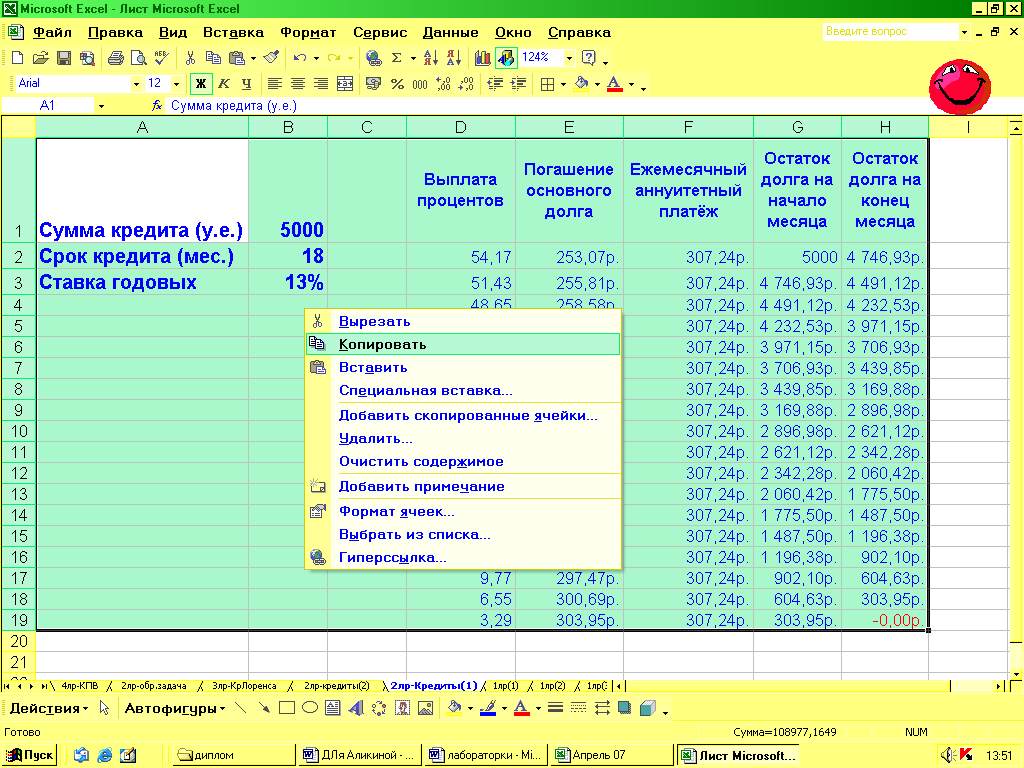
В столбце «Погашение основного долга» долг должен быть равномерно распределен в течение всего срока кредитования. То есть в ячейке Е2 появляется формула '=$G$2/$B$2'. Копируем её на все значения столбца.
Далее правим название третьего столбца, удалив слово «аннуитетный». И Задаем значения столбца с помощью формулы ‘=Е2+D2’.
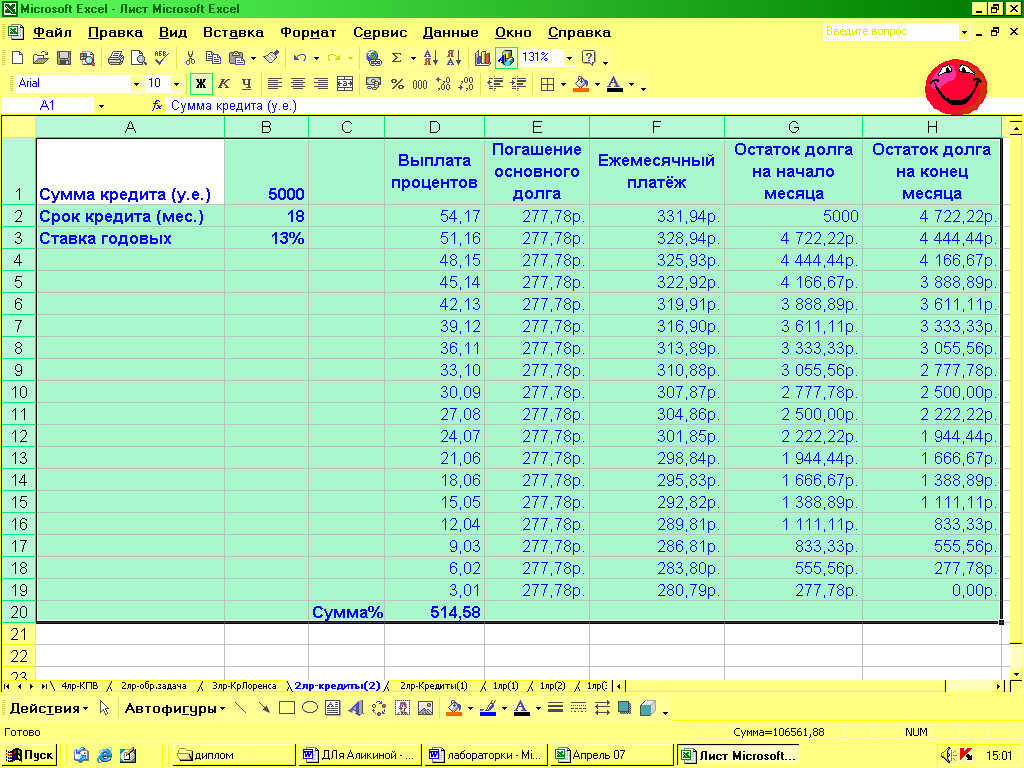
Осталось ответить на вопрос, в каком банке А или Б выгоднее взять кредит? Для ответа на этот вопрос необходимо найти «цену» кредита, или ту сумму, которую мы платим за пользование деньгами. В нашей таблице это Значения столбца «Выплата процентов». Они показывают ежемесячную стоимость кредита. Найдем стоимость кредита за 18 месяцев (весь срок) в обоих банках и сопоставим их значения. Видим, что в банке Б при дифференцированных выплатах плата за пользование кредитом меньше, чем в банке А. Следовательно, взять кредит в банке Б при данных условиях будет выгоднее.
Условия задач для самостоятельного решения:
Банк А предлагает кредит в 7 тыс. у.е. на 18 месяцев под 15% годовых. Выплаты кредита – ежемесячно равными частями (аннуитет). Банк Б предлагает аналогичные условия, но с дифференцированными выплатами (размер ежемесячного платежа по мере погашения долга уменьшается). Дополнительных комиссий в обоих случаях не предусмотрено.
Сколько заёмщик заплатит за кредит банку А и банку Б? Каков будет размер его ежемесячных выплат? В каком банке ему выгоднее взять кредит?
Банк А предлагает кредит в 10 тыс. у.е. на 24 месяца под 14,5% годовых. Выплаты кредита – ежемесячно равными частями (аннуитет). Банк Б предлагает аналогичные условия, но с дифференцированными выплатами (размер ежемесячного платежа по мере погашения долга уменьшается). Дополнительных комиссий в обоих случаях не предусмотрено.
Сколько заёмщик заплатит за кредит банку А и банку Б? Каков будет размер его ежемесячных выплат? В каком банке ему выгоднее взять кредит?
Банк А предлагает кредит в 7 тыс. у.е. на 24 месяца под 10% годовых. Выплаты кредита – ежемесячно равными частями (аннуитет). Банк Б предлагает аналогичные условия, но с дифференцированными выплатами (размер ежемесячного платежа по мере погашения долга уменьшается). Дополнительных комиссий в обоих случаях не предусмотрено.
Сколько заёмщик заплатит за кредит банку А и банку Б? Каков будет размер его ежемесячных выплат? В каком банке ему выгоднее взять кредит?
Банк А предлагает кредит в 20 тыс. у.е. на 18 месяцев под 13,5% годовых. Выплаты кредита – ежемесячно равными частями (аннуитет). Банк Б предлагает аналогичные условия, но с дифференцированными выплатами (размер ежемесячного платежа по мере погашения долга уменьшается). Дополнительных комиссий в обоих случаях не предусмотрено.
Сколько заёмщик заплатит за кредит банку А и банку Б? Каков будет размер его ежемесячных выплат? В каком банке ему выгоднее взять кредит?
