3.3. Матричный.

3.3.1. Большинство задач автоматизации конструирования схем удобно решать при использовании матричного способа представления графов. Квадратная таблица R=//r_i,j//_n*n называется матрицей смежности, если её строки и столбцы соответствуют вершинам графа, а элементы r_i,j образуются по правилу:

- r_i,j = 1, если вершина x_i соединена с вершиной x_j ребром, т.е. x_i смежна x_j;

- r_i,j = 0, в противном случае.

Заметим, что для мультиграфа и смешанного графа задают:

- r_i,j = p, если вершина x_i соединена с вершиной x_j p – числом рёбер;

- r_i,j = 0 в противном случае.

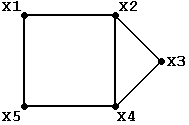
Рисунок 1.

Очевидно, что для неорграфов r_i,j = r_j,i и для их задания можно использовать треугольную матрицу R. Так для графа на рисунке 1 матрица смежности R имеет вид:

R =

	X1	X2	X3	X4	X5
X1	0	1	0	0	1
X2	1	0	1	1	0
X3	0	1	0	1	0
X4	0	1	1	0	1
X5	1	0	0	1	0

Треугольная матрица R’ для этого же графа запишется

R^’ =

	X1	X2	X3	X4	X5
X1	0	1	0	0	1
X2		0	1	1	0
X3			0	1	0
X4				0	1
X5					0

Строки и столбцы матрицы R cоответствуют вершинам графа. На пересечении i-й строки и j-го столбца ставится элемент r_i,j, соответствующий числу рёбер, соединяющих вершины x_i и x_j. Строки и столбцы матрицы R можно нумеровать числами натурального ряда, соответствующими индексам помеченных вершин. Петлям в графе соответствуют элементы r_i,i главной диагонали матрицы R. Преимущесво использования матриц смежности - это простота выполнения преобразований и операций над графами как для конструктора, так и для ЭВМ.

3.3.2. Граф можно задавать также матрицей инциденций B, строки которой соответствуют вершинам графа, столбцы - ребрам. Элементы b_i,j матрицы B для неорграфа могут принимать значения ( 0 или 1 ):

b_i,j = 1, если ребро u_k инцидентно вершине x_i;

b_i,j = 0, если ребро u_k не инцидентно вершине x_i.

Рисунок 2.

Для графа, представленного на рисунке 2, матрица инциденций B имеет вид:

	U1	U2	U3	U4	U5	U6
X1	1	1	0	0	0	0
X2	1	0	1	1	0	0
X3	0	0	0	1	1	0
X4	0	0	1	0	1	1
X5	0	1	0	0	0	1