Практичне заняття № 21. Загальне рівняння лінії другого порядку.
Перетин лінії з прямою. Центр лінії. Рівняння дотичної та нормалі. Основні теоретичні факти.
Розглянемо
алгебраїчну лінію другого порядку
,
задану рівнянням
,
(1)
де
- деякі дійсні числові коефіцієнти,
причому коефіцієнти
одночасно не дорівнюють нулю. Доданки
називають групою
старших
членів,
вираз
- лінійною
частиною,
число
- вільним
членом
рівняння. Розв’язки даного рівняння,
тобто впорядковані пари чисел
на координатній площині задають множину
точок, які утворюють, взагалі кажучи,
деяку лінію. Очевидно, що це лінія другого
порядку.
Рівняння (1) називають загальним рівнянням лінії другого порядку.
Оскільки рівняння (1) містить 6 коефіцієнтів, які визначаються з точністю до сталого множника, то лінія другого порядку задається, взагалі кажучи, 5 точками. У деяких випадках кількість умов, які визначають лінію другого порядку може бути меншою. Наприклад, коло задається трьома точками на ньому, парабола - чотирма.
Введемо в розгляд
символи
,
означивши їх рівностями
,
а також
,
де
та
- координати деякої точки. Вони не складні
для запам’ятання. Зокрема
можна трактувати, як половину похідної
від функції
по змінній
(змінна
при знаходженні похідної вважається
сталою), а
- як половину похідної від функції
по змінній
(у цьому випадку не змінюється
).
Хордою лінії другого порядку назвемо відрізок, який сполучає дві точки на лінії.
Точка
буде серединою хорди, що проходить через
неї у напрямку вектора
,
якщо виконується умова
.
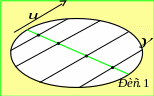
Середини всіх паралельних хорд утворюють пряму (рис. 1). Її рівняння записується у виді
.
Я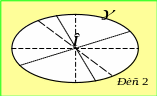
кщо
для лінії існує точка, в якій всі хорди,
що проходять через неї, діляться пополам,
то цю точку називають центром
лінії.
Фактично центр лінії є її центром
симетрії, оскільки разом із будь-якою
точкою лінії, їй належить також точка,
симетрична даній відносно центра. На
рисунку 2 центром лінії
є точка
- середина всіх можливих хорд, що проходять
через неї.
Умовою того, щоб точка була серединою хорд, що проходить через неї, є виконання рівностей
.
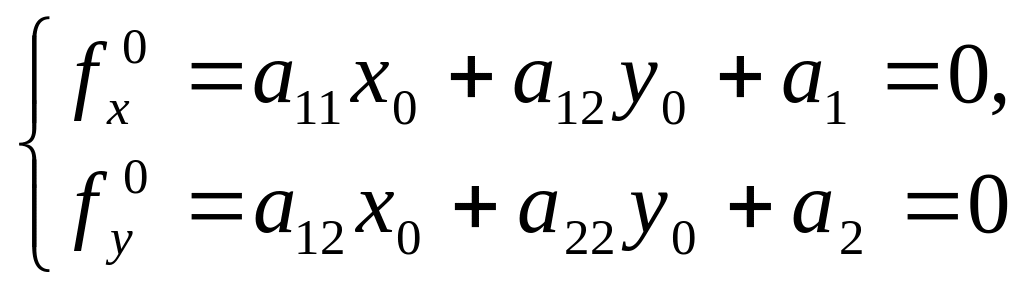(2)
Існування та
кількість розв’язків системи (2) залежить
від визначника
.
Якщо
,
то система має єдиний розв’язок. У цьому
випадку лінія
має єдиний центр і її називають
центральною.
Прикладами таких ліній є еліпс, гіпербола,
лінія другого порядку, яка вироджується
у пару прямих, що перетинаються.
Якщо
,
то система (2) має безліч, або не має
жодного розв’язку. Лінію
в цьому випадку називають нецентральною.
Прикладами таких ліній є парабола, пара
паралельних прямих. В останньому випадку
центри лінії
утворюють пряму, яка є середньою лінією
смужки, утвореної даними паралельними
прямими.
Рівняння
дотичної,
проведеної до лінії
в точці
,
записується у виді
.
(3)
Нормаллю до лінії, проведеній в деякій точці, називають пряму, яка перпендикулярна до дотичної, проведеної у цій же точці. Її рівняння записується у виді
.