Вычисление производной

1. Условие задачи

Найти производную функции на промежутке при шаге дискретизации .

2. Постановка задачи

Производной функции y=f(x) называется конечный предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю:

.

Геометрический смысл производной заключается в том, что производная есть угловой коэффициент (тангенс угла наклона ) касательной, проведенной к кривой в точке с абсциссой x (рис. 11).

Продифференцировать функцию (найти ее производную) можно, используя таблицу производных и правила дифференцирования. Однако в ряде случаев правилами дифференцирования воспользоваться достаточно сложно. Например, когда функция задана таблично или получена в результате наблюдений. В этих случаях прибегают к численным методам дифференцирования.

Рис. 11. Геометрический смысл производной

Численное дифференцирование очень чувствительно к ошибкам, вызванным неточностью исходных данных, отбрасываемых членов ряда и т.д., и поэтому должно применяться с осторожностью.

Существуют различные формулы численного дифференцирования. Из них простейшими являются явные трехточечные формулы, в частности:

(10)

Здесь и – три последовательные точки, – достаточно малый шаг дискретизации. Погрешность вычисления производной по формуле (10) может быть оценена из выражения

,

(11)

где . Когда экспериментальные данные имеют большие погрешности, используют методы дифференцирования по большему числу точек. Примером может являться так называемая формула численного дифференцирования после сглаживания:

.

(12)

3. Решение задачи

Для решения задачи, прежде всего, необходимо ввести данные в рабочую таблицу: в ячейку А2 – первое значение аргумента – 0 (левую границу диапазона), в ячейку А3 – второе значение (левая граница плюс шаг дискретизации – 0,2), затем необходимо скопировать формулу в ячейки А4:А33. Далее в ячейку В2 с помощью мастера функций следует ввести формулу =SIN(А2), которую после скопировать в ячейки B3:B33, например, маркером автозаполнения.

По введенным в рабочую таблицу данным необходимо найти значения производной. Для этого в ячейку С3 вводим формулу дифференцирования (10): =(B4 – B2)/(2*0,2). Протягиванием (за правый нижний угол) копируем ее из ячейки С3 в ячейки С4:С32 (в ячейках С2 и С33 значения производной не определены, так как не заданы значения синуса в ячейках В1 и B34). Получены значения производной (рис. 12).

Вычислить производную подынтегральной функции для вариантов, представленных в табл. 4.

Решение систем линейных уравнений

1. Условие задачи

Решить систему линейных уравнений, используя различные способы:

(13)

2. Постановка задачи

Исходную систему часто представляют в виде AX=B, где A – матрица коэффициентов при неизвестных, X – матрица неизвестных, B – матрица свободных членов.

Матричный способ основан на использовании обратной матрицы: X=A^–1B.

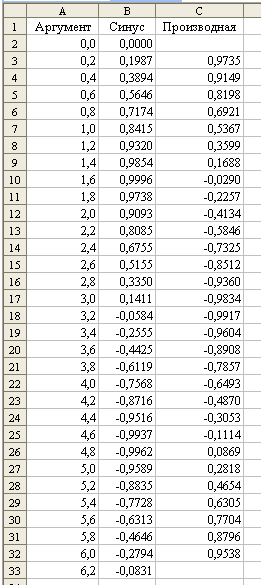
Рис. 12. Значения производной

Метод Крамера для нахождения неизвестных использует определители матриц: X₁=det(AX₁)/det(A); X₂= det(AX₂)/det(A); X₃= det(AX₃)/det(A).

Встроенная команда Поиск решения меню Сервис позволяет найти неизвестные, добиваясь равенства матрицы свободных членов (правой части) произведению матрицы коэффициентов на матрицу неизвестных (левой части), причем, варьировать можно лишь значениями неизвестных.