
- •Microsoft excel в инженерно-экономических расчетах
- •Решение уравнения
- •Табулирование функции
- •1. Условие задачи
- •2. Постановка задачи
- •3. Решение задачи
- •Вычисление значения функции
- •1. Условие задачи
- •2. Постановка задачи
- •3. Решение задачи
- •Вычисление определенного интеграла
- •1. Условие задачи
- •2. Постановка задачи
- •3. Решение задачи
- •Вычисление производной
- •1. Условие задачи
- •2. Постановка задачи
- •3. Решение задачи
- •Решение систем линейных уравнений
- •1. Условие задачи
- •2. Постановка задачи
- •3. Решение задачи
- •Обработка экспериментальных данных
- •1. Условие задачи
- •2. Постановка задачи
- •3. Решение задачи
- •Задачи многомерной оптимизации с ограничениями
- •1. Условие задачи
- •2. Постановка задачи
- •3. Решение задачи
- •1. Условие задачи
- •2. Постановка задачи
- •3. Решение задачи
- •1. Условие задачи
- •2. Постановка задачи
- •3. Решение задачи
- •Дифференциальные уравнения первого порядка
- •1. Условие задачи
- •2. Постановка задачи
- •3. Решение задачи
- •Комплексные числа
- •1. Условие задачи
- •2. Постановка задачи
- •Обработка статистических данных
- •1. Условие задачи
- •Гистограмма
- •Библиографический список
- •Оглавление
3. Решение задачи
Создадим макет таблицы и подготовим исходные данные для расчета (рис. 9). Для этого впишем значения нижнего (ячейка А3) и верхнего (ячейка В3) пределов интегрирования в соответствии с заданным интегралом (1); зададим количество отрезков N (ячейка С3) и рассчитаем величину шага Н по формуле (2).
Далее в ячейке А5 зададим начальное значение аргумента X, равное нижнему пределу интегрирования (=А3); в ячейку А6 запишем формулу расчета приращения аргумента (=А5+$D$3), указав абсолютную адресацию для ячейки, в которой записана величина шага и скопируем формулу из ячейки А6 в нижележащие ячейки вплоть до ячейки А25, в которой значение аргумента станет равным 6, т. е. верхнему пределу интегрирования заданного интеграла. Столбец со значениями аргумента подготовлен.


Рис. 9. Подготовка таблицы
Теперь заполним столбец со значениями функции. В ячейку В5 запишем выражение для подынтегральной функции (=А5^2) и скопируем его в нижележащие ячейки.
Переходим к составлению расчетной формулы метода прямоугольников. Знак суммы в выражении (5) для Excel непонятен, поэтому выражение надо записать иначе и для накопления суммы использовать рекуррентную зависимость:
|
(8) |
Здесь каждое последующее значение суммы Si+1 рассчитывается на основании предыдущего Si плюс следующий член последовательности HY(Xi). Обратите внимание, что значение аргумента берется от предыдущего шага Xi. Чтобы не произошло накопление ошибки, первоначальную сумму надо обнулить, поэтому в ячейку С5 запишем ноль. Саму рекуррентную зависимость, выраженную в адресах, запишем в ячейку С6 (=C5+B5*$D$3). Затем скопируем формулу из ячейки С6 в ячейки диапазона С7:С25. Получим ряд промежуточных сумм, а в ячейке С25 будет представлен окончательный результат (рис. 10). Он равен 66,69.
Для реализации метода трапеций также организуем накопление площадей, используя рекуррентную зависимость:
|
(9) |
Это означает, что на каждом шаге к сумме, накопленной за предыдущие шаги, добавляется площадь очередной трапеции. В ячейку D6 запишем выражение для суммы площадей на втором шаге (=D5+(B5+B6)*$D$3/2). Скопируем выражение в ячейки диапазона D7:D25. Результат представлен на рис. 10.
Интересно сравнить результаты, полученные методом прямоугольников (66,69) и трапеций (72,09), с точным решением определенного интеграла (72), а так же исследовать влияние на точность вычислений числа отрезков N, на которые разбивается интервал интегрирования [a, b].
Варианты заданий представлены в табл. 4.
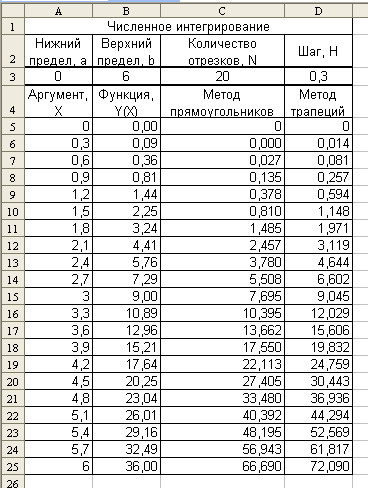
Рис. 10. Результаты численного определения интеграла
Таблица 4
№ вар. |
Исходные данные |
№ вар. |
Исходные данные |
1 |
|
16 |
|
2 |
|
17 |
|
3 |
|
18 |
|
4 |
|
19 |
|
Окончание табл. 4
№ вар. |
Исходные данные |
№ вар. |
Исходные данные |
5 |
|
20 |
|
6 |
|
21 |
|
7 |
|
22 |
|
8 |
|
23 |
|
9 |
|
24 |
|
10 |
|
25 |
|
11 |
|
26 |
|
12 |
|
27 |
|
13 |
|
28 |
|
14 |
|
29 |
|
15 |
|
30 |
|
