Вычисление значения функции

1. Условие задачи

Вычислить значение функции в зависимости от условия. Использовать встроенную функцию ЕСЛИ

2. Постановка задачи

Задана функция y(x), имеющая разрывы в точках – 1 и 1. Для вычисления ее значений удобно использовать встроенную функцию ЕСЛИ, позволяющую наряду с единственным условием в качестве аргумента использовать другие функции, в том числе функцию ЕСЛИ. Такая вложенная структура позволяет учесть все точки разрыва.

3. Решение задачи

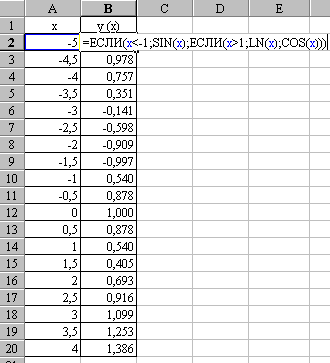
В одном из столбцов (рис. 6) располагают значения аргумента.

В данном случае – в виде прогрессии с постоянным шагом, что вовсе не обязательно. Весь диапазон пунктом Вставить… команды Имя меню Вставка назван вполне понятным именем x. Соседний столбец заполнен с помощью маркера автозаполнения одной формулой:

=ЕСЛИ(x<–1;SIN(x);ЕСЛИ(x>1;LN(x);COS(x))).

В формуле используется вложенная функция ЕСЛИ, которая и вычисляет значение Y(x) в зависимости от значения самого аргумента x.

Рис. 6. Вычисление значений функции по условию

Варианты заданий представлены в табл. 3.

Таблица 3

№ вар.	Исходные данные	№ вар.	Исходные данные
1		16
2		17
3		18
4		19

Продолжение табл. 3

№ вар.	Исходные данные	№ вар.	Исходные данные
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27

Окончание табл. 3

№ вар.	Исходные данные	№ вар.	Исходные данные
13		28
14		29
15		30

Вычисление определенного интеграла

1. Условие задачи

Вычислить методами прямоугольников и трапеций определенный интеграл

.

(1)

2. Постановка задачи

Как известно, определенный интеграл

(2)

представляет собой площадь фигуры, образуемой кривой подынтегральной функции , отрезком оси абсцисс, ограниченным нижним (a) и верхним (b) пределами интегрирования, и перпендикулярами, восстановленными из концов интервала интегрирования до пересечения с кривой функции . Вид подынтегральной функции определяет геометрическую форму образующейся фигуры.

Площадь такой фигуры в силу разнообразия видов подынтегральных функций, как правило, не может быть точно вычислена по известным аналитическим зависимостям. Поэтому фигуру разбивают на простые геометрические формы, для нахождения площади которых, имеются аналитические зависимости. Это могут быть, например, прямоугольники или трапеции. Подсчитанные площади простых фигур затем суммируются. В рамках погрешности метода эта сумма принимается за значение определенного интеграла.

Метод прямоугольников

Интервал интегрирования [a, b] разбивается на N равных отрезков, длина каждого из которых

.

(3)

Величина Н называется шагом интегрирования.

В результате разбиения получаем на оси абсцисс ряд равноудаленных друг от друга точек X₀, X₁, Х₂, ..., Х_n. Точки Х₀ и Х_n совпадают соответственно с нижним (a) и верхним (b) пределами интегрирования. Восстанавливаем из точек разбиения перпендикуляры до пересечения с кривой подынтегральной функции и завершаем построение прямоугольников (рис. 7).

Площадь каждого прямоугольника S_i выражается как произведение основания, равного шагу разбиения Н, на высоту, равную значению подынтегральной функции Y(X) в точке:

.

(4)

Просуммируя площади и вынеся за знак суммы значение шага Н получим итерационную формулу:

.

(5)

Рис. 7. Геометрическая интерпретация метода

прямоугольников

Метод трапеций

Интервал интегрирования также разбивается на N отрезков, а искомая фигура заменяется совокупностью прямоугольных трапеций (рис. 8).

Рис. 8. Геометрическая интерпретация метода

трапеций

Площадь трапеции, как известно, определяется произведением полусуммы оснований на высоту. В нашем случае имеем

(6)

Просуммировав площади элементарных фигур и проведя элеентарные преобразования, можно записать формулу для приближенного вычисления интеграла:

(7)