2

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Уфимский государственный нефтяной технический университет»

Кафедра «Машины и аппараты химических производств»

УЧЕБНО-МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению практических работ № 4, 5 по дисциплине

«Основы надежности оборудования»

РЕКОМЕНДОВАНО

к использованию

НМС УГНТУ

«___»_________200_г.,

протокол №__.

Зам. председателя НМС

Е.И.Ишемгужин_________

2006

УДК

ББК

К

Габбасова А.Х. Учебно-методическое указание по выполнению практических работ № 4, 5 по дисциплине «Основы надежности оборудования». – Уфа: УГНТУ, 2006. – 17 с.

Учебно-методическое указание предназначено для студентов направления 150400 – Технологические машины и оборудование и специальности 130603 – Оборудование нефтегазопереработки, специализации 171701 – Проектирование, монтаж, эксплуатация и ремонт оборудования, специализации 171702 – Надежность технологических систем и оборудования

Содержание

		С
Введение		4
Практические работы № 4, 5. Выбор оптимального числа резервных элементов в системе в случае нагруженного резерва		5
Комплект заданий к практическим работам № 4, 5		11
Список использованных источников		15
Приложения		16

Введение

Для повышения надежности сложных систем и отдельных объектов имеются четыре основных пути:

- повышение надежности элементов системы;

- конструктивные мероприятия повышения надежности;

- коренное изменение принципа функционирования системы данного назначения;

- введение различного вида избыточности.

Избыточность - это дополнительные средства и возможности сверх минимально необходимых для выполнения объектом заданных функций. Методом повышения надежности объекта введением избыточности является резервирование.

Различат три типа структурного резервирования: нагруженный резерв, облегченный резерв, ненагруженный резерв.

При параллельном соединении элементов в системе всегда можно создать сложную систему с высоким уровнем надежности из элементов с низкой надежностью.

Но тогда возникает вопрос: сколько же надо поставить резервных элементов, чтобы получить заданную надежность, считая резерв нагруженным?

Расчет ненагруженного резерва более сложен, поэтому часто используют схему нагруженного резерва, что приводит к заниженным значениям надежности.

Однако методики и решения для расчета системы с нагруженным резервом вполне могут быть использованы при выборе оптимальной схемы, так как если данный вариант имеет лучшую надежность при нагруженном резерве, то в действительности в случае ненагруженного резерва этот вариант тоже будет иметь лучшие показатели.

Практические работы № 4, 5 Выбор оптимального числа резервных элементов в системе в случае нагруженного резерва

Цель. Достижение заданной надежности системы с наименьшими затратами.

Задача определения количества резервных элементов для получения заданной надежности системы с нагруженным резервом в простейшем случае решается очень быстро. Выражение для параллельного соединения (в смысле надежности) одинаковых элементов

Р_с(t)= 1 – [1 – Р_э(t)]^х,

где х - число необходимых элементов;

Р_с(t) - заданная величина надежности системы;

P_э(t) - надежность элементов.

Расчет структурной схемы двух последовательно соединенных групп агрегатов с резервированием является более сложной задачей. Однако именно такие схемы часто встречается в промышленности.

Задача 4.1

Необходимо спроектировать компрессорную станцию, представляющую собой систему компрессоров (рисунок 4.1), состоящую из группы компрессоров низкого давления (КНД) и группы компрессоров высокого давления (КВД).

КНД КВД

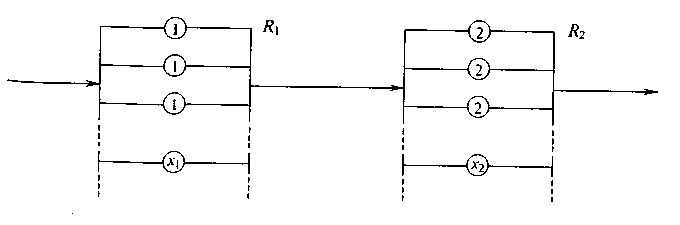
Рисунок 4.1 – Схема системы компрессоров

Компрессоры низкого давления характеризуются интенсивностью отказов ₁=2,2·10^-5 1/ч., компрессоры высокого давления - интенсивностью отказов ₂=1,0·10^-5 1/ч.

Требуется определить необходимое число n₁ компрессоров первой и число n₂ компрессоров второй групп, чтобы вероятность безотказной работы за заданное время t=10 000 ч. не была ниже минимального допустимого значения Р_{с min доп.}=0,960.

Комбинацию выбрать по критерию минимальных затрат на сооружение станции.

Стоимость компрессора низкого давления – С₁=1 денежных единиц, компрессора высокого давления - С₂=3 денежных единиц.

Резервирование считать упрощенно как нагруженное.

Решение

1). Определить надежность компрессоров через 10 000 часов при данных значениях параметра потока отказов _i:

- для КНД

Р₁(10 000) = e^-1·t = = 0,80;

- для КВД

Р₂(10 000) = e^-2·t = = 0,90.

2). Расчеты надежности в отдельных группах при различном числе резервных агрегатов.

Расчеты произвести в таблице 4.1.

Таблица 4.1 – Расчеты в отдельных группах

Число компрессоров в группе	Группы компрессоров
	КНД	КВД
2	1-(1-Р1)2 = 0,960	1-(1-Р2)2 = 0,990
3	1-(1-Р1)3 = 0,992	1-(1-Р2)3 = 0,999

3). Рассчитать надежности систем последовательно соединенных групп компрессоров. Построим расчетную матрицу комбинаций (таблица 4.2).

Таблица 4.2 - Расчетная матрица комбинаций

Группа КВД		Группа КНД
		n1 = 1 КНД	n1 = 2 КНД	n1 = 3 КНД
		0,800	0,960	0,992
n2 = 1 КВД	0,900	-	-	-
n2 = 2 КВД	0,990	-	0,950	0,980
n2 = 3 КВД	0,999	-	0,960	0,990

В таблице 4.2 нет смысла заполнять ячейки, отмеченные прочерком, ибо один из сомножителей выражения общей надежности системы здесь меньше заданного числа Р_{с min доп.}=0,96, значит, мы не сможем достичь нужного показателя надежности в этих комбинациях.

4). Выбор оптимальной комбинации по критерию наименьших затрат

Таблица 4.2 показывает, что заданному условию Р_с  Р_{с min доп.} удовлетворяют три комбинации:

- первая комбинация - это n₁=2, n₂=3;

- вторая комбинация - n₁=3, n₂=2;

- третья комбинация - n₁=3, n₂=3.

Из этих трех комбинаций мы должны выбрать оптимальную по критерию наименьших затрат. Третью комбинацию можно сразу отбросить, поскольку она, однозначно, дороже двух первых.

Полные затраты на оборудование по двум первым комбинациям определим по формуле:

S_i = C₁·n₁ + C₂·n₂

где i – номер комбинации.

Для первой комбинации (Р_с1 = 0,96)

S₁ = C₁·n₁ + C₂·n₂ = 1·2 + 3·3 = 11 д.ед.

Для второй комбинации (Р_с2 = 0,98)

S₂ = C₁·n₁ + C₂·n₂ = 1·3 + 3·2 = 9 д.ед.

Вывод.

Видно, что S₂ < S₁ и, следовательно, мы принимаем вторую комбинацию. В данном частном случае эта комбинация хороша не только тем, что он требует меньших затрат, но он обеспечивает и более высокий уровень вероятности безотказной работы: Р_с2 = 0,98 > Р_с1 = 0,96.