2

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Уфимский государственный нефтяной технический университет»

Кафедра «Машины и аппараты химических производств»

УЧЕБНО-МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению практической работе № 2 по дисциплине

«Основы надежности оборудования»

РЕКОМЕНДОВАНО

к использованию

НМС УГНТУ

«___»_________200_г.,

протокол №__.

Зам. председателя НМС

Е.И.Ишемгужин_________

2006

УДК

ББК

К

Габбасова А.Х. Учебно-методическое указание по выполнению практической работы № 2 по дисциплине «Основы надежности оборудования». – Уфа: УГНТУ, 2006. – 13 с.

Учебно-методическое указание предназначено для студентов направления 150400 – Технологические машины и оборудование и специальности 130603 – Оборудование нефтегазопереработки, специализации 171701 – Проектирование, монтаж, эксплуатация и ремонт оборудования, специализации 171702 – Надежность технологических систем и оборудования

Содержание

		С
Введение		4
Практическая работа № 2. Расчет показателей надежности по эмпирическим данным при малой выборке		5
Комплект заданий к практической работе № 2		9
Список использованных источников		10
Приложения		11

Введение

Одним из основных понятий надежности является отказ – событие, заключающееся в нарушении работоспособности объекта. Отказы, возникающие в машинах, носят многопричинный, случайный характер.

Случайная величина – величина, которая в результате испытаний может принять значение, причем нельзя заранее предсказать, какое именно.

К категории случайных величин относятся показатели надёжности. Поэтому в теории надёжности широко используются методы теории вероятностей и математической статистики. Статистиками называются оценки параметров распределения, полученные по результатам испытаний.

Статистическая обработка данных испытаний производится для оценок требуемых параметров надежности.

Случайные величины, расположенные в возрастающем порядке с указанием вероятности их появления называют распределением случайных величин.

Соотношение, устанавливающее связь между значением случайных величин и вероятностью их появления, называют законом распределения.

В процессе жизненного цикла в объекте происходят различные физические процессы. Задача теории надежности заключается в выборе такого закона распределения, который наиболее полно отражает эти физические законы.

Практическая работа № 2. Расчет показателей надежности по эмпирическим данным при малой выборке

Цель. Для возможности прогнозирования надежности объекта выбрать закон распределения при заданных значениях наработки до отказа ряда аналогичных объектов.

В теории надежности используются следующие законы распределения:

- нормальный закон распределения;

- закон распределения Вейбула-Гнеденко;

- экспоненциальный закон.

Закон распределения может быть представлен в виде числовых осей, таблиц, графиков и аналитически. Законы распределения случайных величин описываются следующими функциями: отказности F(t), безотказности Р(t), интенсивности (t). Для каждого закона распределения эти функции имеют свой вид. К примеру, функция (t) имеет специфическую форму и часто используется для определения вида распределения:

- если (t) постоянна во времени, то принимается гипотеза об экспоненциальном законе;

- (t) имеет минимум или максимум в середине интервала, то принимается нормальный закон распределения;

- если (t) убывает или возрастает с увеличением t, то имеет место закон Вейбула-Гнеденко

Задача 2.1

Выявить закон распределения, который отражает с высокой степенью достоверности реальную картину потери надежности объекта, работающего на нефтеперерабатывающем предприятии. Статистическая проработка позволила установить наработки до отказов ряда аналогичных объектов, ч: 123, 218, 230, 210, 234, 217, 200, 157. Оценить параметры закона распределения.

Решение

1) Определяем к какому типу относится статистическая выборка (малая или большая). Количество испытанных объектов (объем выборки) N = 8 < 20 – малая выборка.

2) Строим вариационный ряд наработки

t₁ < t₂ < t₃ < t₄ < … < t_n, (2.1)

где t_i - наработка до отказа i – го объекта, ч.

123 157 200 210 217 218 230 234

3) Для каждого значения определяем показатели надежности P_i(t), F(t), _i(t). Результаты сводятся в таблицу 2.1.

В таблице 2.1 оценка вероятности безотказной работы в i-й по порядку момент времени t_i определяется:

P(t_i)= , (2.2)

где i – номер по порядку в вариационном ряду.

Оценка вероятности безотказной работы в первый по порядку момент времени t₁:

P(123)=

Вероятность отказа в i-й по порядку момент появления отказа t_i оценивается как:

, или F(t_i)=1 - P(t_i). (2.3)

Вероятность отказа в первый по порядку момент появления отказа t₁:

F(123)=1 - P(123) = 1 - 0,917 = 0,083.

Интенсивность отказов в I-й по порядку момент времени ti определяется следующим образом:

, (2.4)

где t_i+1 – наработка до отказа в следующий по порядку момент времени.

Интенсивность отказов в первый по порядку момент времени t₁=123 ч:

=

Таблица 2.1 – Результаты расчетов показателей надежности

Номер по порядку	1	2	3	4	5	6	7	8
ti, ч	123	157	200	210	217	218	230	234
Pi(t)	0,917	0,798	0,680	0,560	0,440	0,320	0,202	0,083
F(t)	0,083	0,202	0,320	0,440	0,560	0,680	0,798	0,917
i(t)	0,0038	0,0035	0,0175	0,0310	0,2730	0,0310	0,1470	-

4) Строим гистограммы P_i(t), F(t) и график изменения _i(t) во времени (рисунок 2.1). По виду графика изменения _i(t) во времени высказываем гипотезу о законе распределения.

Поскольку график изменения _i(t) во времени имеет минимум и максимум в середине интервала (см. рисунок 2.1), то предполагаем, что имеет место нормальный закон распределения случайных величин наработок до отказа.

5) Оценка параметров предполагаемого закона распределения

Среднее арифметическое значение случайной величины

. (2.5)

.

Среднее квадратическое отклонение случайной величины:

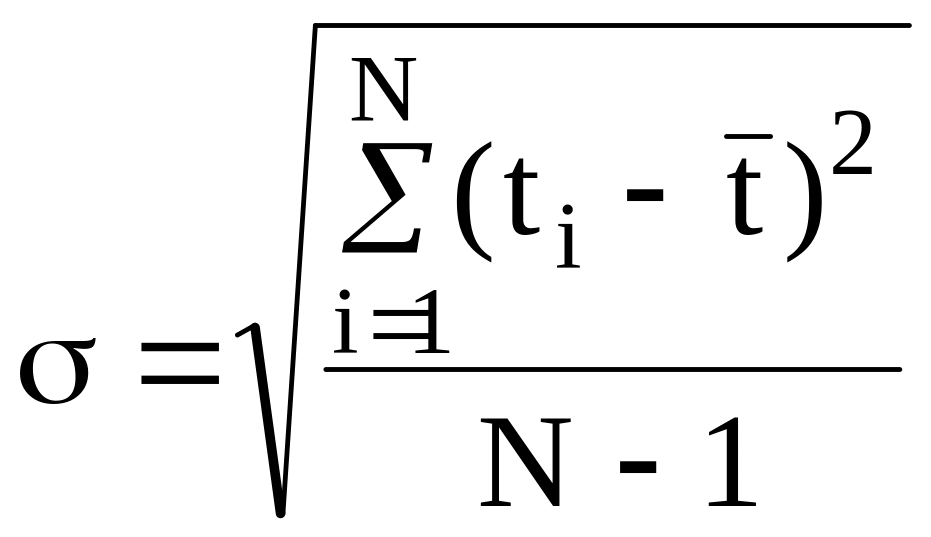. (2.7)

.

Коэффициент вариации

. (2.6)

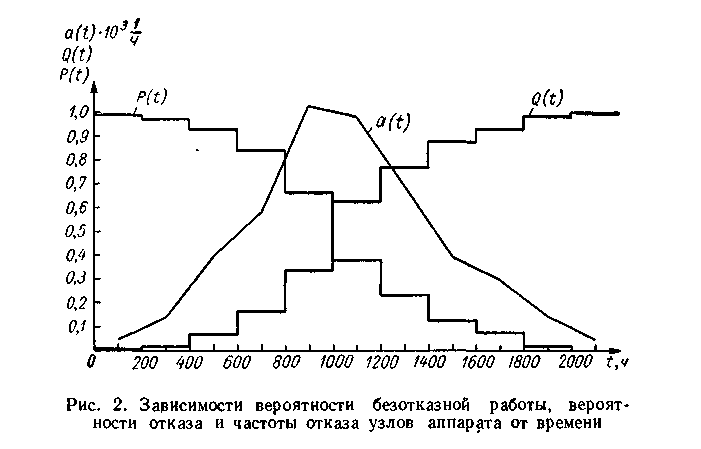
Рисунок 2.1 - Гистограммы P_i(t), F(t) и график изменения _i(t) во времени

6) Проверка гипотезы о предполагаемом законе распределения по критерию Колмогорова

Строим теоретическую функцию распределения значения вероятности отказа F*(t) – выравнивающую кривую изменения вероятности отказа во времени (см. рисунок 2.1).

Критерий Колмогорова определяется из графиков как наибольшее абсолютное отклонение между статистической F(t) и теоретической F*(t) функциями вероятностей отказов (см. рисунок 2.1):

D_max=max |F*(t) - F(t)|. (2.8)

D_max= max |F*(t) - F(t)|=0,07.

Определяем условную интенсивность:

.

Далее по справочным данным (приложение А) по значению * определяется условная вероятность Р(*).

Если вероятность Р(*) не является малой ( 0,5), то гипотеза о предполагаемом законе распределения не противоречит опытным данным.

Итак,

Р(*) = Р(0,2) = 1,0 > 0,5.

Вывод

Поскольку условная вероятность Р(*) > 0,5, то гипотеза о предполагаемом законе распределения не противоречит опытным данным. Для возможности прогнозирования надежности объекта принимаем нормальный закон распределения случайных величин.