Фотограмметрія(10)

1. Побудувати перспективи двох горизонтальних відрізків, які паралельні лінії напрямку знімання (лнз)

1. В ідрізки продовжують до пересічення з віссю перспективи. Отримані точки належать двом площинам – площині предмета та площині знімка.

2. На площині знімка знаходять положення головної точки сходу І і будують лінію істинного горизонту h_ih_i перпендикулярно головній вертикалі.

3. Через центр проекції S проводять промінь, паралельний заданим відрізкам. Він розташований в площині істинного горизонту. Пересічення цього променя з лінією h_ih_i визначає точку сходу І' зображень відрізків.

4. З’єднують прямими лініями точку І' з точками, отриманими на осі перспективи. Ці лінії на знімку є лініями, що йдуть від осі перспективи, через задані відрізки до нескінченності.

Проводять проектуючі промені через точки, що визначають відрізки. Їх пересічення з побудованими на знімку лініями і визначає шукане зображення.

2. Побудувати перспективи двох горизонтальних відрізків, які створюють з лінією напрямку знімання кут φ.

1. Відрізки продовжують до пересічення з віссю перспективи. Отримані точки належать двом площинам – площині предмета та площині знімка.

2. На площині знімка знаходять положення головної точки сходу І і будують лінію істинного горизонту h_ih_i перпендикулярно головній вертикалі.

3. Через центр проекції S проводять промінь, паралельний заданим відрізкам. Він розташований в площині істинного горизонту. Пересічення цього променя з лінією h_ih_i визначає точку сходу І' зображень відрізків.

4. З ’єднують прямими лініями точку І' з точками, отриманими на осі перспективи. Ці лінії на знімку є лініями, що йдуть від осі перспективи, через задані відрізки до нескінченності.

5. Проводять проектуючі промені через точки, що визначають відрізки. Їх пересічення з по­бу­до­ва­ни­ми на знімку лініями і ви­зна­чає шукане зображення.

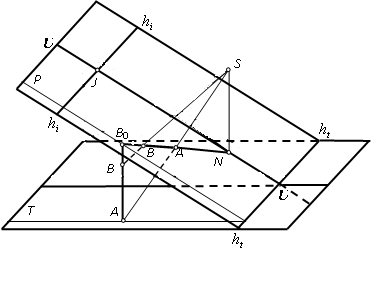
3. Побудувати перспективу прямовисної прямої

Точка сходу зображень вертикальних (прямовисних) прямих співпадає із точкою надиру n. Пересічення B_o відрізка АВ з площиною знімка знаходиться на сліді вертикальної площини, що проходить через пряму АВ і паралельна площині головного вертикала. Тому відрізок NB₀ є зображення нескінченного прямовисного променя із точки В₀. Проекції точок А та В належить цьому відрізку, значить для їх побудови достатньо провести проектуючі промені.

4. Визначити масштаб планового знімка якщо відомі фокусна відстань АФА та висота польоту над середньою площиною ділянки знімання - f = 100 мм, Н_ф = 4 500 м

Розв’язок: Із формули отримаємо:

5. Визначити базис фотографування якщо відомі масштаб знімання та відстань між центрами проекцій .

_{Розв’язок:}

6. Визначити відстань між маршрутами за умови знімання та відстань між осями маршрутів .

_{Розв’язок:}

.

7. Визначити величину лінійного зміщення на горизонтальному аерофотознімку, спричиненого рельєфом місцевості в точці надиру

Відповідь: Для точки надиру величина радіус вектора тоді

8. Визначити величину радіусу корисної площі знімка в якій похибки за рельєф не перевищують графічної точності плану якщо аерофотознімання виконується для створення топографічного плану м-бу 1:5000, висота фотографування становить 3600м, фокусна віддаль 150мм, максимальне перевищення над середньою площиною ділянки 150м.

Відповідь: графічна точність плану становить 0,1мм, в м-бі плану – 5м.

Масштаб знімка

Коефіцієнт збільшення знімка при цьому становитиме

Графічна точність плану становить 0,1мм, в масштабі знімка – 0,021мм.

Радіус корисної площі знімка розраховують за формулою:

9. Визначити величину лінійного зміщення для планового аерофотознімка, спричиненого його нахилом для точки що розташована на головній вертикалі знімка якщо відомо що ; ;

Відповідь: Для точок що лежать на головній вертикалі знімка , для планових знімків синус кута вираженого в радіанах рівний самому куту отже: