
- •Связь между напряженностью и потенциалом.
- •Расчет полей при помощи теоремы Гаусса.
- •Электрический диполь
- •Диполь во внешнем поле
- •2)Проводники в электростатическом поле
- •3)Электрическое поле в диэлектриках.
- •Вектор электрического смещения и поляризации.
- •Примеры на вычисление поля в диэлектриках
- •Условия на границе двух диэлектриков.
- •Энергия электростатического поля
- •4)Постоянный электрический ток.
- •Уравнение непрерывности
- •Соединение проводников.
- •Закон Ома для неоднородного участка цепи.
- •Правила кирхгофа
- •5)Основы зонной теории
- •Контакт двух полупроводников
- •Вольт-амперная характеристика полупроводниковых диодов.
1)Электрический заряд –скалярная физическая величина, определяющая интенсивность электрического взаимодействия частиц (тел).
Электрическое поле – форма материи, обладающая особыми физическими свойствами, главное из которых заключается в следующем положении: на электрические заряды, помещенные в это поле, действуют силы, пропорциональные этим зарядам.
Закон Кулона – это закон взаимодействия двух неподвижных точечных зарядов. Он гласит: электрическая сила взаимодействия между двумя заряженными неподвижными точечными телами пропорциональна произведению их зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль прямой линии, проведенной от одного заряда к другому.
F= k=1/4πε0
, ε0=8,85*10-12
Ф/м –эл.постоянная
k=1/4πε0
, ε0=8,85*10-12
Ф/м –эл.постоянная
Сила
взаимодействия м/у двумя точечными
зарядами в наиболее общей (векторной)
форме:
F= Q1
,Q2-точечн.заряды,
r-расст.м/у
зарядами, радиус-вектор
r.
Q1
,Q2-точечн.заряды,
r-расст.м/у
зарядами, радиус-вектор
r.
Напряженность- силовая характеристика поля( вект.величина)
E= =
= r
–
расстояние от заряда Q
до
точки поля, определенного радиус-вектором
r,
r
–
расстояние от заряда Q
до
точки поля, определенного радиус-вектором
r,
 -пробный
заряд, Q-точечный
заряд
-пробный
заряд, Q-точечный
заряд
Потенциал и разность потенциалов – энергетические характеристики электрического поля. Они являются скалярными величинами и могут быть положительными или отрицательными по знаку. Физическим смыслом обладает только разность потенциалов, так как она отражает работу перемещения заряда, исполненную силами поля.
φ=
- =
= -потенциал
любого электростатического поля,
-потенциал
любого электростатического поля,
Edr – скалярные произведения векторов соответственно F∙dr и E∙dr, где dr – вектор элементарного смещения.
∆φ=φ1-φ2=- -
-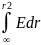 =
= -Разность
потенциалов двух точек, определенных
радиус-векторами r1
и r2.
-Разность
потенциалов двух точек, определенных
радиус-векторами r1
и r2.
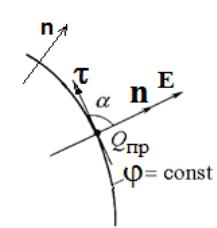
Связь между напряженностью и потенциалом.
E=En= - вектор
напряженности равен по модулю первой
производной потенциала по нормали к
эквипотенциальной поверхности.
- вектор
напряженности равен по модулю первой
производной потенциала по нормали к
эквипотенциальной поверхности.
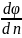 -называется
градиентом потенциала, обозначается
grad
или
φ,
поэтому E
gradφ
или
E
φ.
-называется
градиентом потенциала, обозначается
grad
или
φ,
поэтому E
gradφ
или
E
φ.
 E
E
 i
i
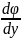 j
j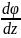 k
k
Теорема Гаусса-Остроградского
ФЕ= –
интегральная форма, ФЕ
–поток
вектора Е. ρ-объемная плотность эл.
зарядов.(Если поле образовано системой
дискретно распределенных зарядов, то
поток вектора электрического поля
через любую замкнутую поверхность в
пустоте равен алгебраической сумме
зарядов, заключенных внутри этой
поверхности, деленной на электрическую
постоянную)
–
интегральная форма, ФЕ
–поток
вектора Е. ρ-объемная плотность эл.
зарядов.(Если поле образовано системой
дискретно распределенных зарядов, то
поток вектора электрического поля
через любую замкнутую поверхность в
пустоте равен алгебраической сумме
зарядов, заключенных внутри этой
поверхности, деленной на электрическую
постоянную)
divE ρ /ε0-дифференциальная
Расчет полей при помощи теоремы Гаусса.
1.
Напряженность
электрического поля, созданного
равномерно заряженной сферой.
Дано: радиус сферы R0,
его заряд Q,
расстояние
точки пространства A от центра
сферы
O равно r
.
Существует два
 различных
варианта вычисления: точка А
находится
во внутренней части сферы (r1
≤R0)
или снаружи (r2
≥ R0).Внутри
сферы, поле не возникает,потому что нет
зарядов в сферическом
пространстве
радиуса r1
< R0.
Следовательно,Е
= 0 и E
=
0.Найдем модуль E
в
точке A снаружи сферы E=
различных
варианта вычисления: точка А
находится
во внутренней части сферы (r1
≤R0)
или снаружи (r2
≥ R0).Внутри
сферы, поле не возникает,потому что нет
зарядов в сферическом
пространстве
радиуса r1
< R0.
Следовательно,Е
= 0 и E
=
0.Найдем модуль E
в
точке A снаружи сферы E= =
=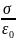
 -радиус
сферы, σ-поверхностная плотность(Q/S)
-радиус
сферы, σ-поверхностная плотность(Q/S)
2. Поле бесконечно длинного цилиндра радиуса R0
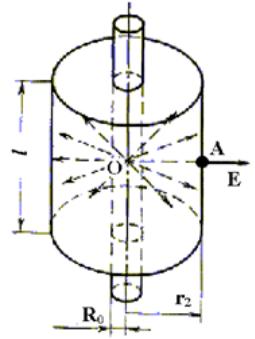
E σR0 / ε0 r2 λ/ 2πR0) R0/ ε0r2 λ/ 2πε0r2
λ- линейная плотность
3. Напряженность поля, созданного бесконечно протяженной плоскостью, равномерно заряженной с поверхностной плотностью

E E1 E2 σ /2ε0 и вывод: поле вокруг бесконечной равномерно заряженной плоскости – однородное.
4. Поле создано двумя равномерно заряженными, параллельными,бесконечно протяженными плоскостями. Плотности заряда плоскостей 1 и 2 (знаки зарядов произвольные). Применяя принцип суперпозиции, находим два результата для напряженности поля:
пространство между плоскостями E E1 E2 σ1-σ2 2ε0 и
пространство локализованно вне плоскостей E E1 E2 σ1+σ2/ 2ε0

Электрический диполь
Электростатическая
система, состоящая из двух точечных
зарядов,одинаковых по модулю, но
противоположных по знаку, называется
электрическим
диполем
(рис. 6). Вектор l
,
проведенный от отрицательного заряда
-Q
к
положительномузаряду+Q,называетсz
осью диполя. Основным параметром диполя
служит вектор электрического дипольного
момента p
Ql
(векторы
![]()
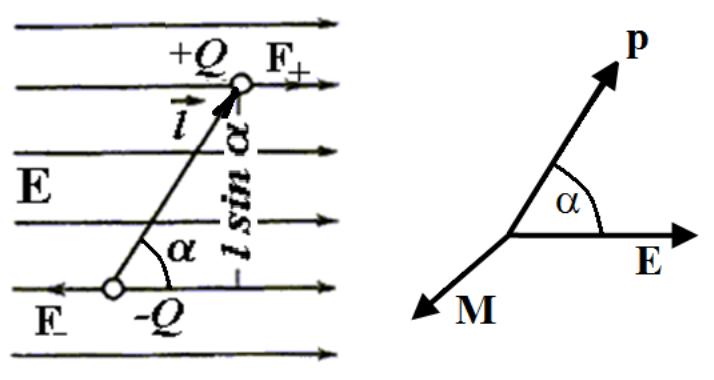 Также
созда.ется момент М пары сил F+
и
F-
Также
созда.ется момент М пары сил F+
и
F-
Диполь во внешнем поле
![]() Найдем
момент сил, действующих на диполь в
однородном электрическом поле. Пусть
положения положительного и отрицательного
зарядов относительно центра диполя
характеризуются векторами r+ и r- ,
соответственно. Тогда, в соответствии
с определением момента сил, имеем
Найдем
момент сил, действующих на диполь в
однородном электрическом поле. Пусть
положения положительного и отрицательного
зарядов относительно центра диполя
характеризуются векторами r+ и r- ,
соответственно. Тогда, в соответствии
с определением момента сил, имеем
![]()
![]()
Если диполь находится в неоднородном внешнем электрическом поле, то равнодействующая сил, действующих на положительный и отрицательный заряды диполя оказывается не равной нулю:
![]()
.
