Явление самоиндукции.

Если Lпри изменениях силы тока остается постоян­ной, то

ЭДС индукции, возникающая в самом же контуре, называется ЭДС самоиндукции, а само явление –самоиндукция. При изменении тока в контуре пропорционально меняется^[2] и магнитный поток через поверхность, ограниченную этим контуром^[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это явление и называется самоиндукцией. Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока  : .

Коэффициент пропорциональности   называется коэффициентом самоиндукции илииндуктивностью контура (катушки).

Индуктивность проводника.

При любом изменении тока в проводнике его собственное магнитное поле также изменяется. Вместе с ним изменяется и поток магнитной индукции, пронизывающий поверхность, охваченную контуром проводника. В результате в этом контуре индуцируется ЭДС. Это явление называется явлением самоиндукции.

В соответствии с законом Био-Савара-Лапласа индукция магнитного поля В пропорциональна силе тока I в проводнике. Отсюда следует, что поток магнитной индукции   и сила тока I также пропорциональны друг другу:

Коэффициент пропорциональности L называют индуктивностью проводника. За единицу индуктивности в СИ принимают индуктивность такого проводника, у которого при силе тока 1А создается поток магнитной индукции, равный 1Вб. Эту единицу называют Генри, Гн.

Индуктивность проводника зависит от его формы и размеров, а также от магнитных свойств окружающей его среды (магнитной проницаемости μ). Заметим при этом, что линейная зависимость между   и I остается справедливой и в том случае, когда μ зависит от напряженности магнитного поля Н, а значит, от I (например, ферромагнитная среда). В этом случае индуктивность L также зависит от I.

Для длинного прямого (или квазилинейного) провода кругового сечения индуктивность выражается приближенной формулой^[19]:

где   − магнитная постоянная,  относительная магнитная проницаемость внешней среды (которой заполнено пространство (для вакуума  ),   - относительная магнитная проницаемость материала проводника,   - длина

провода,   - радиус его сечения

Взаимная индуктивность

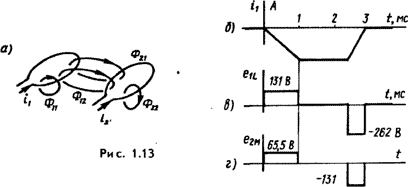
На рис. 1.13, а изображены два контура. По первому течет ток i₁, по второму - i₂. Поток, создаваемый первым контуром Ф₁, частично замыкается, пронизывая только первый контур Ф₁₁, минуя второй, частично пронизывая и второй контур Ф₁₂. Чтобы рисунок был более понятным, на нем изображено только по одной силовой линии каждого потока

Ф₁ = Ф₁₁ + Ф₁₂

Аналогично, поток, создаваемый вторым контуром:

Ф₂ = Ф₂₂ + Ф₂₁

Если первый контур имеет ω₁ витков, то потокосцепление первого контура ω₁ (Ф₁ ± Ф₂) = ω₁ Ф₁ ± ω₁ Ф₂₁ = Ψ₁ ± Ψ₂₁. Потокосцепление второго контура (число витковω₂)

ω₂ (Ф₂ ± Ф₂₁) = Ψ₂ ± Ψ₁₂

Знаки "+" соответствуют согласному направлению потока от своего тока и потока, создаваемого током в соседнем контуре. Знаки "–" соответствуют несогласному (встречному) направлению потоков (для этого один из токов должен изменить направление). Потокосцепление Ψ₂₁ пропорционально току i₂, а Ψ₁₂ - току i₁

Ψ₂₁ = ω₁ Ф₂₁ = Мi₂,

Ψ₁₂ = ω₂ Ф₁₂ = Мi₁

Коэффициент пропорциональности М (Гн) называют взаимной индуктивностью

M = Ψ₂₁ / i₂ = Ψ₁₂ / i₁          (1.41)

Она зависит от взаимного расположения, числа витков, геометрических размеров контуров (катушек) и от магнитной проницаемости μ_a сердечников, на которых они намотаны. Если μ_a = const, то от величины токов М не зависит.