2.2. Непрерывно детерминированные модели (д - схемы).
D-схема = Dynamic =динамическая схема – математическая схема, отражающая динамику изучаемой системы, т.е. ее поведение во времени. Непрерывные детерминированные модели (D-схемы) используют дифференциальные уравнения.
Если неизвестные - функции многих переменных, то уравнения называются — уравнения в частных производных. Если неизвестные функции одной независимой переменной, то имеют место обыкновенные дифференциальные уравнения.
Математическое соотношение для детерминированных систем в общем виде:
(7).
Диф. уравнения, Д - схемы являются математическим аппаратом теории систем автоматического регулирования, управления.
В качестве примера D-схемы рассмотрим модель Лотки – Вольтерры системы «хищник-жертва», которая имеет вид:
Рассматривается модель Лотки-Вольтерры системы «хищник-жертва»:
где
–
количество жертв,
–
количество хищников,
t – время,
a, b, c, g – коэффициенты, отражающие взаимодействия между видами:
a – коэффициент рождаемости жертв,
g – коэффициент рождаемости хищников,
c – коэффициент убыли хищников,
b – коэффициент гибели жертв при встрече с хищником,
Точка
покоя модели Лотки-Вольтерры может
быть получена путем приравнивания нулю
правых частей уравнений системы:
,
откуда нетривиальная точка покоя равна
,
.
Управляемая система Лотки-Вольтерра имеет вид:
Линеаризуем рассматриваемую систему:
- линеаризованная система
Сделаем замену переменных: 
- положительно определенная матрица
(диагональная для простоты), 
- неотрицательно определенная матрица
(диагональная для простоты)
Построим функционал Лагранжа
- оптимальное решение
,
- произвольные функции
Подставим в функционал x, u и J:
Возьмем производную и приравняем ее нулю:
Возьмем по частям интеграл:
Тогда
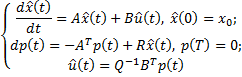
Двухточечная краевая задача
Для ее решения в линейном случае используется метод прогонки.
Используем метод прогонки для решения системы ДУ:
Собираем коэффициенты при 
:
Собираем свободные члены:
В точке 
:
Поскольку 
,
то 
Это задача Коши, которую надо решать в обратном времени.
Решение этого однородного линейного ДУ с граничным условием, равным точке покоя есть точка покоя:
С учетом этого 
Тогда уравнение замкнутой системы (управляемой):
Уравнение для 
имеет квадратичную правую часть. Это
уравнение Риккати (Riccati).
– симметричная матрица
Если заменить
на 
,
то система остается управляемой, но
управление становится немного хуже.
Тогда получим субоптимальное управление:
Для линеаризованной системы управления
(или 
)
является оптимальным (субоптимальным).
Поскольку 
,
то 
(или 
), то для нелинейной системы получаем
(или 
),
КОЛЛОКВИУМ по 3 лекциям