
- •Часть 1. Моделирование систем Лекция №1.
- •Глава 1. Понятие моделирования.
- •1.1. Моделирование сложных систем
- •1.2. Принцип системного подхода в моделировании систем
- •1.3. Характеристики моделей систем.
- •1.4. Этапы моделирования систем
- •1. Постановка цели моделирования.
- •2. Построение модели м.
- •Лекция №2
- •1.5. Классификация видов моделирования систем.
- •3.1. Мысленное моделирование может быть реализовано в виде наглядного, символического и математического.
- •Лекция №3.
- •Часть 2. Математические схемы моделирования систем
- •2.1. Основные подходы к построению мм систем.
- •2.2. Непрерывно детерминированные модели (д - схемы).
- •Лекция №4.
- •2.3. Дискретно-детерминированные модели (f-схемы). Конечные автоматы
- •2.4. Дискретно-стохастические модели (p-схемы). Вероятностные автоматы
- •Пример у-детерминированного автомата
- •Лекция №5.
- •4.3. Непрерывно-стохастические модели (q - схемы).
- •1.1Методы теории массового обслуживания.
- •К лассификация моделей смо
- •Лекция №6.
- •Поведенческие свойства сетей Петри
- •1. Достижимость.
- •2. Ограниченность.
- •3. Активность.
- •4. Обратимость и базовое состояние.
- •Задача о конечности функционирования сети Петри
- •Пример использования сети Петри при анализе состояний дедлока.
- •Лекция №7. Комбинированные модели (а-схемы). Сложные системы
- •Лекция №8.
- •Часть 3. Моделирование систем с использованием типовых математических схем.
- •3.1. Блочная (модульная) концепция моделирования
- •3.2. Принципы построения моделирующих алгоритмов
- •3.3. Моделирование процесса функционирования систем на базе q-схем.
- •Часть 4. Статистическое моделирование систем Лекция №9. Общая характеристика и сущность метода статистического моделирования
- •1. Детерминированная задача вычисления интеграла
- •2. Стохастическая задача вычисления математического ожидания и дисперсии f(X,y).
- •Лекция 10. Псевдослучайные последовательности. Датчики случайных чисел.
- •2. Метод серединных квадратов.
4. Обратимость и базовое состояние.
Сети Петри обратима, если для любой маркировки М из R(M0) маркировка М0 достижима от М. Иными словами, в обратимой сети всегда можно вернуться к начальной маркировке (состоянию). Во многих задачах необязательно возвращаться в начальное состояние, но достаточно иметь возможность вернуться в базовое состояние. Поэтому условие обратимости можно ослабить и определить понятие базового состояния. Маркировка М' называется базовым состоянием, если она достижима от любой маркировки М из R(M0).
Задача о конечности функционирования сети Петри
Одна из основных проблем в теории сетей Петри - задача о конечности функционирования сети (о достижении тупиковой разметки).
Суть проблемы состоит в ответе на вопрос для данной конкретной сети - существует ли такая последовательность срабатывания переходов, которая приводит сеть к тупиковой разметке (т.е. разметке, при которой ни один переход не может сработать)?
Более того, анализ сетей позволяет утверждать, что ненкоторые сети всегда приходят к тупиковой разметке. Это математическое утверждение (теорема!) может быть строго доказано.
Заметим, что хотя некоторые сети обязательно останавливается, т.е. достигают тупиковой разметки, но сами эти тупиковые разметки могут быть различны.
Свойство достижения конечной разметки присуще далеко не всем сетям. Существуют сети, всегда приходящие к тупиковой разметке, сети, никогда не попадающие в тупик, сети, которые могут остановиться, а могут и нет.
Инструментальные средства моделирования с помощью сетей Петри позволяют запустить сеть Петри в работу (провести имитационное моделирование) и посмотреть, достигнет лисеть тупиковой разметки или нет.
Пример использования сети Петри при анализе состояний дедлока.
Сети Петри оказались удобным средством для анализа такого свойства параллельной системы, как наличие или отсутствие дедлоков. Состояние дедлока возникает, когда запрос ресурсов в системе не может быть удовлетворен и система останавливается (ни один переход не может сработать).
Рассмотрим пример на рис. 6. Сеть А определяет циклическое неограниченное срабатывание переходов t1, t2, t3. При срабатывании переходы t2 и t3 потребляют единицу ресурса из места р3 каждый. Можно представить себе для определенности, что место р3 содержит два участка памяти (буферы), которые операционная система может динамически выделять программе по ее запросу. Пока процесс, управляемый сетью А, выполняется один, ситуации дедлока не возникает. Но если появляется идентичный процесс, выполняющийся параллельно А и управляемый сетью В (рис. 6), тогда возникает конкуренция за ресурс в месте р3.
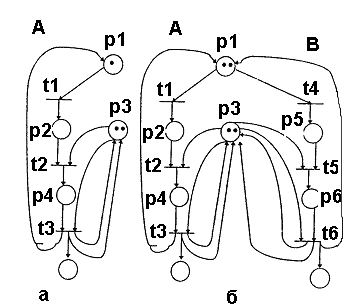
Рис 6. Пример сети Петри, моделирующей состояние системы без дедлока (а) и с дедлоком (б).
Ситуация дедлока возникает при такой последовательности срабатываний переходов сети: t1, t4, t2, t5. И в этом состоянии имеем дедлок: ни один переход не может сработать. Однако сеть будет нормально функционировать, если в позиции p1 оставить одну фишку, т.е. разрешить выполняться либо процессу А, либо процессу В, но не обоим одновременно.
