Поведенческие свойства сетей Петри
1. Достижимость.
Достижимость является фундаментальным понятием, необходимым для изучения динамических свойств любой системы. Запуск разрешенного перехода приводит к перераспределению фишек в сети (смене маркировки) по правилу перехода. Последовательности запусков соответствует последовательность маркировок. Маркировка Мn достижима из маркировки М0, если существует последовательность запусков, приводящих от М0 к Мn.
Множество всех маркировок, достижимых в сети (N, M0) от М0, обозначается как R(N, M0), или просто R(M0).
Таким образом, проблема достижимости в сетях Петри заключается в том, чтобы при заданной маркировке Мn в сети (N, M0) установить принадлежность Mn к множеству R(M0).
2. Ограниченность.
Другое направление исследования функционирования сети Петри связано с изменением количества фишек в конкретной или произвольной позиции в процессе функционирования сети.
Сеть Петри называется К-ограниченной, или просто ограниченной, если для любой маркировки, достижимой от маркировки М0, количество фишек в любой позиции не превышает некоторого числа К, т .е. М(р) <= К для любого р и любой маркировки М, принадлежащей R(M0). Сеть Петри (N, M0) называется безопасной, если она 1-ограниченна.
Позиции сети Петри часто моделируют буферы или регистры, служащие для хранения промежуточных результатов. Проверка ограниченности или безопасности сети гарантирует отсутствие переполнения буферов или регистров при любой фактической последовательности запусков переходов.
Безопасная сеть никогда, не допустит, чтобы в переменную было положено новое значение, если старое еще не было использовано по назначению. Нарушения этого правила часто являются причиной ошибок в параллельных программах.
В другой интерпретации переход может представлять некоторое устройство. Устройство может (но не должно) сработать, если выполнились все входные условия. Если несколько переходов готовы сработать, то срабатывает один из них (любой), или некоторые из них, или все.
Рассмотрим пример конвейера. Пусть есть три обрабатывающих устройства t0, t1, t2 организованные в виде конвейера. Это могут быть, например, станки на заводе или функциональные устройства конвейерного процессора и вообще любой конвейер, в котором каждое обрабатывающее устройство выполняет лишь часть общей работы, а результат будет выработан лишь последним из них.
Особенностью нашего конвейера является ограниченность емкости мест p1 и р2; место p1 может вместить лишь два результата (место p1 сети является 2-ограниченым) предшествующего этапа работы конвейера (вырабатывается переходом t0 ), а место p2 - 3-ограниченным. Символ n в месте р0 означает наличие n фишек в нем, n - целое положительной число.
Сеть Петри, обеспечивающая необходимое прямое управление, приведена на рис. Понятно, что в месте p1 не может накопиться более 2 фишек при любых порядках срабатывания переходов сети.
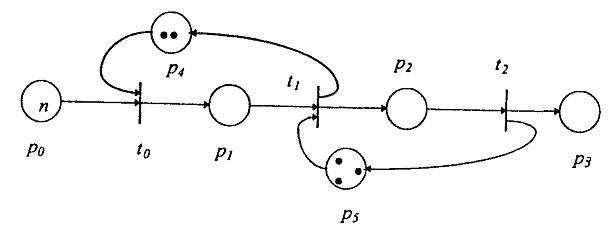
Рис. 5. Пример сети Петри, моделирующей работу конвейера.
3. Активность.
Понятие активности тесно связано с отсутствием возможности взаимной блокировки (тупиковых ситуаций) в операционной системе. Сеть Петри активна (или, что эквивалентно, маркировка М0 сети Петри активна), если независимо от достигнутой от М0 маркировки, для любого перехода существует последовательность дальнейших запусков, приводящая к его запуску. Это означает, что для активной сети Петри при любой последовательности запусков полностью исключена возможность взаимной блокировки.