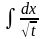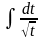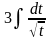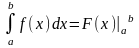04.2. Критические точки, максимумы и минимумы
51. Задание {{ 128 }} ТЗ № 128
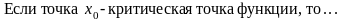
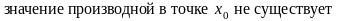
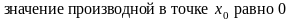
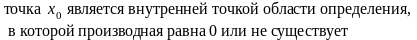
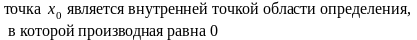
52. Задание {{ 129 }} ТЗ № 129
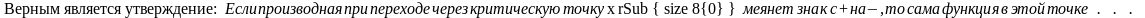
имеет максимум
имеет минимум
экстремума не имеет
иной ответ
53. Задание {{ 130 }} ТЗ № 130
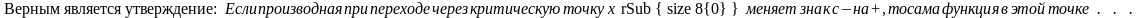
имеет минимум
имеет максимум
экстремума не имеет
иной ответ
04.3. Примеры применения производной к исследованию функции
54. Задание {{ 156 }} ТЗ № 156
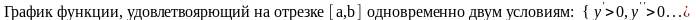
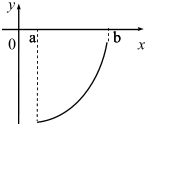
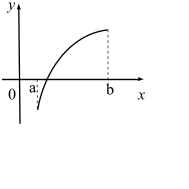
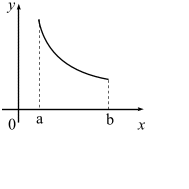
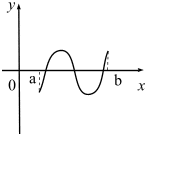
04.4. Наибольшее и наименьшее значения функции
55. Задание {{ 77 }} ТЗ № 77
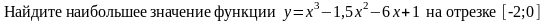
max y(x)=y(-1)=4,5
min y(x)=y(-2)=1
max y(x)=y(-0,5)=2
min y(x)=y(-3)=0
56. Задание {{ 78 }} ТЗ № 78
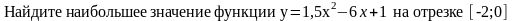
min y(x)=y(-1)=4,5
max y(x)=y(-2)=19
max y(x)=y(-0,5)=2
min y(x)=y(-3)=0
57. Задание {{ 79 }} ТЗ № 79
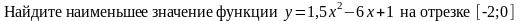
max y(x)=y(1)=-2
max y(x)=y(-1)=12
min y(x)=y(3)=64
min y(x) = y(0) = 1
58. Задание {{ 80 }} ТЗ № 80
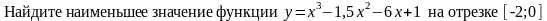
max y(x)=y(2)=56
max y(x)=y(-1)=12
min y(x)=y(3)=64
min y(x) = y(-2) = -1
05. Первообразная
05.1. Определение первообразной
59. Задание {{ 131 }} ТЗ № 131
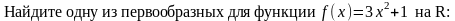
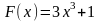
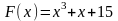
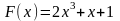
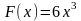
60. Задание {{ 132 }} ТЗ № 132
Функция F называется первообразной для функции f на заданном промежутке, если для всех х из этого промежутка
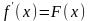
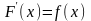
05.2. Основное свойство первообразной
61. Задание {{ 133 }} ТЗ № 133
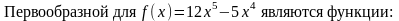
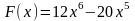
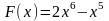
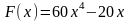
62. Задание {{ 134 }} ТЗ № 134
Найдите общий вид первообразной для функции f(x) = x + cos x
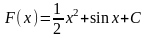
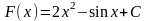
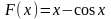
05.3. Правила вычисления первообразной
63. Задание {{ 135 }} ТЗ № 135
Если функция F первообразна для функции f, а функция G первообразна для функции g, то F+G есть первообразная для
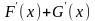
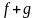
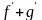
64. Задание {{ 136 }} ТЗ № 136
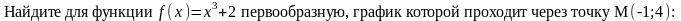
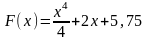
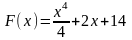
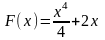
06. Интеграл
06.1. Интеграл. Формула Ньютона - Лейбница
65. Задание {{ 137 }} ТЗ № 137
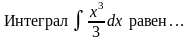
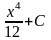
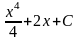
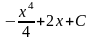
66. Задание {{ 138 }} ТЗ № 138
3
5
-3
6
67. Задание {{ 139 }} ТЗ № 139
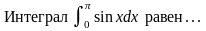
2
1
-1
0
68. Задание {{ 140 }} ТЗ № 140
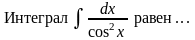
tg x + C
-x-tg x+C
x+ctg x+C
-x+ctg x+C
69. Задание {{ 141 }} ТЗ № 141
-0,5cos2x+C
0,5cos2x+C
2cos2x+C
cos2x+C
70. Задание {{ 142 }} ТЗ № 142
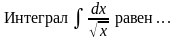
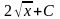
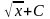
71. Задание {{ 143 }} ТЗ № 143
Формула Ньютона-Лейбница имеет вид:
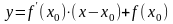
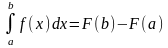
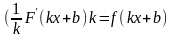
72. Задание {{ 147 }} ТЗ № 147
Установите соответствие
Уравнение касательной
|
|
Формула Ньютона-Лейбница |
|
Определённый интеграл |
|
Производная первообразной функции |
|
06.2. Площадь криволинейной трапеции
73. Задание {{ 144 }} ТЗ № 144
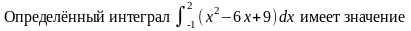
21
24
18
27
74. Задание {{ 145 }} ТЗ № 145
162 м
78 м/с
162 м/с
78 м
75. Задание {{ 146 }} ТЗ № 146
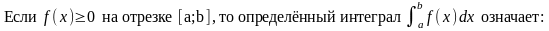
скорость прямолинейного движения тела
перемещение тела
ускорение прямолинейного движения тела
площадь соответствующей криволинейной трапеции
76. Задание {{ 150 }} ТЗ № 150
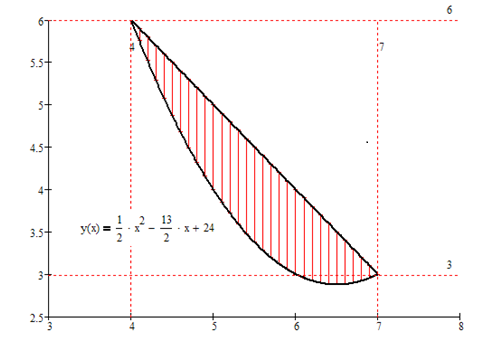
Площадь заштрихованной части фигуры, изображенной на чертеже, задана интегралом...
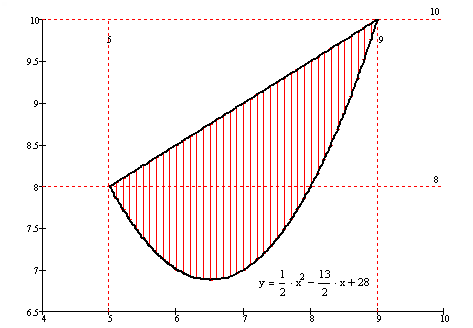
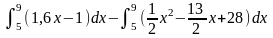
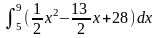
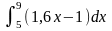
77. Задание {{ 151 }} ТЗ № 151
Площадь заштрихованной части фигуры, изображенной на чертеже, вычисляется формулой:
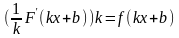
78. Задание {{ 153 }} ТЗ № 153
Площадь фигуры, представленной на чертеже, вычисляется по формуле:
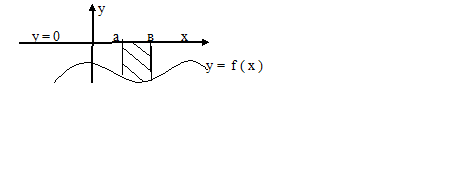
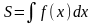
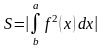
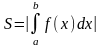
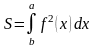
79. Задание {{ 155 }} ТЗ № 155
