- •Содержание заданий контрольной работы
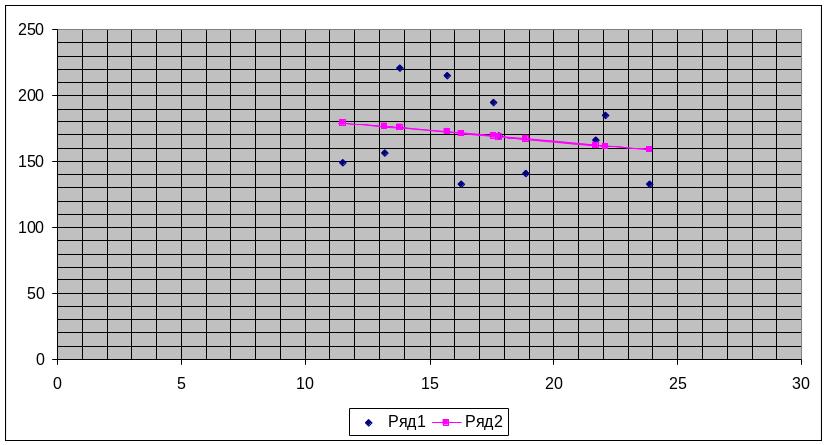
- •Построить корреляционное поле и предложить гипотезу о связи исследуемых факторов, сделать предположения о наличии выбросов;
- •1.2 Определить коэффициенты корреляции;
- •1.3 Оценить статистическую надежность и значимость вычисленных коэффициентов корреляции
- •Сделать итоговые выводы.
- •1.1.1 Расчет в Excel по формулам, реализующим метод наименьших квадратов;
- •Расчет с помощью функции линейн с расшифровкой полученных результатов;
- •1.1.4 Инструмент «Регрессия»
- •1.2 Оценить статистическую надежность результатов регрессионного моделирования для чего построить доверительные интервалы коэффициентов регрессии по t-критерию Стьюдента
- •Оценить качество уравнения регрессии с помощью средней ошибки аппроксимации.
- •1.5 Дать с помощью общего (среднего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- •Сделать итоговые выводы.
1.1.1 Расчет в Excel по формулам, реализующим метод наименьших квадратов;
Решение задач с использованием формул
Параметры a и b линейной регрессии
![]()
рассчитываются с помощью метода наименьших квадратов. Для этого составим систему нормальных уравнений (1).
По
исходным данным определим
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() в
расчетной таблице 1.
в
расчетной таблице 1.
Таблица 1 Расчет показателей парной линейной регрессии и корреляции
№ |
x |
y |
x*y |
|
|
|
|
|
|
1 |
21,7 |
166 |
3602,2 |
470,89 |
27556 |
162,246879 |
0,022609162 |
14,08592 |
17,64 |
2 |
22,1 |
185 |
4088,5 |
488,41 |
34225 |
161,569093 |
0,126653552 |
549,0074 |
21,16 |
3 |
18,9 |
141 |
2664,9 |
357,21 |
19881 |
166,991384 |
0,184336057 |
675,552 |
1,96 |
4 |
17,8 |
169 |
3008,2 |
316,84 |
28561 |
168,855297 |
0,000856233 |
0,020939 |
0,09 |
5 |
17,6 |
195 |
3432 |
309,76 |
38025 |
169,19419 |
0,132337488 |
665,9398 |
0,01 |
6 |
15,7 |
215 |
3375,5 |
246,49 |
46225 |
172,413675 |
0,19807593 |
1813,595 |
3,24 |
7 |
13,8 |
221 |
3049,8 |
190,44 |
48841 |
175,633161 |
0,205279817 |
2058,15 |
13,69 |
8 |
13,2 |
156 |
2059,2 |
174,24 |
24336 |
176,64984 |
0,13237077 |
426,4159 |
18,49 |
9 |
11,5 |
149 |
1713,5 |
132,25 |
22201 |
179,530432 |
0,20490223 |
932,1073 |
36 |
10 |
23,9 |
133 |
3178,7 |
571,21 |
17689 |
158,519054 |
0,191872586 |
651,2221 |
40,96 |
11 |
16,3 |
133 |
2167,9 |
265,69 |
17689 |
171,396996 |
0,288699215 |
1474,329 |
1,44 |
итого |
192,5 |
1863 |
32340,4 |
3523,43 |
325229 |
1863 |
1,68799304 |
9260,426 |
154,68 |
Сред нее |
17,5 |
169,3636 |
2940,036 |
320,3118 |
29566,27273 |
169,363636 |
0,153453913 |
|
|
Режим проверки формул
№ |
x |
y |
x*y |
x2 |
y2 |
|
|
|
|
1 |
21,7 |
166 |
=B2*C2 |
=B2*B2 |
=C2*C2 |
=$F$25+$F$24*B2 |
=ABS((C2-G2)/C2) |
=(C2-G2)^2 |
=(B2-$B$14)^2 |
2 |
22,1 |
185 |
=B3*C3 |
=B3*B3 |
=C3*C3 |
=$F$25+$F$24*B3 |
=ABS((C3-G3)/C3) |
=(C3-G3)^2 |
=(B3-$B$14)^2 |
3 |
18,9 |
141 |
=B4*C4 |
=B4*B4 |
=C4*C4 |
=$F$25+$F$24*B4 |
=ABS((C4-G4)/C4) |
=(C4-G4)^2 |
=(B4-$B$14)^2 |
4 |
17,8 |
169 |
=B5*C5 |
=B5*B5 |
=C5*C5 |
=$F$25+$F$24*B5 |
=ABS((C5-G5)/C5) |
=(C5-G5)^2 |
=(B5-$B$14)^2 |
5 |
17,6 |
195 |
=B6*C6 |
=B6*B6 |
=C6*C6 |
=$F$25+$F$24*B6 |
=ABS((C6-G6)/C6) |
=(C6-G6)^2 |
=(B6-$B$14)^2 |
6 |
15,7 |
215 |
=B7*C7 |
=B7*B7 |
=C7*C7 |
=$F$25+$F$24*B7 |
=ABS((C7-G7)/C7) |
=(C7-G7)^2 |
=(B7-$B$14)^2 |
7 |
13,8 |
221 |
=B8*C8 |
=B8*B8 |
=C8*C8 |
=$F$25+$F$24*B8 |
=ABS((C8-G8)/C8) |
=(C8-G8)^2 |
=(B8-$B$14)^2 |
8 |
13,2 |
156 |
=B9*C9 |
=B9*B9 |
=C9*C9 |
=$F$25+$F$24*B9 |
=ABS((C9-G9)/C9) |
=(C9-G9)^2 |
=(B9-$B$14)^2 |
9 |
11,5 |
149 |
=B10*C10 |
=B10*B10 |
=C10*C10 |
=$F$25+$F$24*B10 |
=ABS((C10-G10)/C10) |
=(C10-G10)^2 |
=(B10-$B$14)^2 |
10 |
23,9 |
133 |
=B11*C11 |
=B11*B11 |
=C11*C11 |
=$F$25+$F$24*B11 |
=ABS((C11-G11)/C11) |
=(C11-G11)^2 |
=(B11-$B$14)^2 |
11 |
16,3 |
133 |
=B12*C12 |
=B12*B12 |
=C12*C12 |
=$F$25+$F$24*B12 |
=ABS((C12-G12)/C12) |
=(C12-G12)^2 |
=(B12-$B$14)^2 |
итого |
=СУММ(B2:B12) |
=СУММ(C2:C12) |
=СУММ(D2:D12) |
=СУММ(E2:E12) |
=СУММ(F2:F12) |
=СУММ(G2:G12) |
=СУММ(H2:H12) |
=СУММ(I2:I12) |
=СУММ(J2:J12) |
средне |
=B13/11 |
=C13/11 |
=D13/11 |
=E13/11 |
=F13/11 |
=G13/11 |
=H13/11 |
|
|
Система нормальных уравнений составит:
![]()
Решив систему, получим: a = 199,02; b = -1,69
Уравнение линейной регрессии имеет вид:
![]() .
.
![]() .
.
Параметры уравнения можно определить и по следующим формулам:
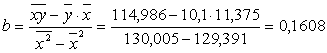 -1,69447
-1,69447
![]() =
169,3636+1,69447*17,5=199,0168
=
169,3636+1,69447*17,5=199,0168
Величина коэффициента регрессии b = -1,69447
означает, что с ростом численности безработных граждан на тысячу человек общий коэффициент зарегистрированных преступлений в расчете на 100 тыс. чел. населения, увеличится в среднем в 1,69447 раз.
Поле корреляции