Ответ неверный!
С увеличением температуры положение максимума смещается вправо в сторону больших скоростей, площадь под кривой не изменяется, следовательно, величина максимума убывает.
Закрыть данную подсказку.
с уменьшением температуры величина максимума функции уменьшается
Ответ неверный!
С уменьшением температуры положение максимума смещается влево в сторону меньших скоростей, площадь под кривой не изменяется, следовательно, величина максимума возрастает.
Закрыть данную подсказку.
при изменении температуры положение максимума не изменяется
Решение:
Полная вероятность равна: , т.е. площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости , при которой функция максимальна, следует, что при повышении температуры максимум функции сместится вправо.
Молярная
теплоемкость идеального газа при
постоянном давлении равна
где
–
универсальная газовая постоянная. Число
вращательных степеней свободы молекулы
равно …
Решение:
Молярные
теплоемкости
и
в
изохорном и изобарном процессах
соответственно равны:
и
.
Сравним:
.
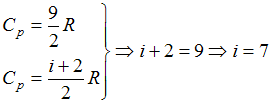Сумма
числа степеней свободы
может
быть представлена как
;
где
число
степеней свободы поступательного
движения
;
число
степеней свободы вращательного движения,
которое может быть равно
;
–
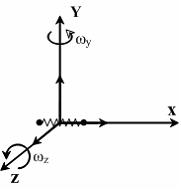
число степеней свободы колебательного
движения, минимальное количество которых
равно 1 (см. рис.).
Следовательно,
и
.
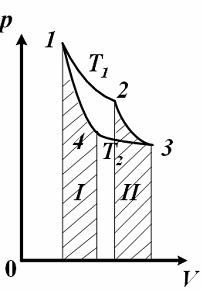
На
диаграмме
изображен
цикл Карно для идеального газа.
Для
величины работы адиабатического
расширения газа
и
адиабатического сжатия
справедливо
соотношение …
работы невозможно сравнить
Ответ неверный!
Используйте первый закон термодинамики и изменение внутренней энергии в этих процессах.
Закрыть данную подсказку.
Ответ неверный!
Процессы
и
–
это процессы адиабатического сжатия
и адиабатического расширения, а
работы этих процессов, согласно первому
закону термодинамики, определяются
изменениями внутренней энергии газа,
которые зависят только от изменения
температуры.
Закрыть данную подсказку.
Решение:
Цикл
Карно состоит из двух изотерм
(изотермического расширения
при
температуре
и
изотермического сжатия
при
температуре
)
и двух адиабат (адиабатического расширения
и
адиабатического сжатия
).
При адиабатическом расширении
и
адиабатическом сжатии
теплообмен
с окружающей средой отсутствует, и
поэтому работы расширения
и
сжатия
совершаются
за счет изменения внутренней энергии
и
.
Следовательно,
работы газа в
адиабатических процессах
и
равны
по величине:
,
а на
-диаграмме
графически определяются площадями
и
заштрихованных
фигур под графиками соответствующих
процессов, и эти площади равны
.