Контрольные вопросы
Объясните отличия графа и дерева.
Что такое цикл?
Что такое путь?
Что такое ациклический путь?
Что такое двоичное дерево?
Назовите способы представления графов и деревьев в Прологе.
Что такое структура в Пролое?
Что такое терм и функтор?
Для чего используются структуры?
Приложение 7а
Основные сведения о структурах данных
Аргументы выражений Пролога называются термами. Существует три вида термов:
Константа - Атом, записываемый как слово, начинающееся с маленькой буквы, произвольная группа символов, заключенных в двойные кавычки или число.
Переменная - записывается как слово, начинающееся с большой буквы, слово, начинающееся со знака подчеркивания или сам знак подчеркивания.
Составной терм (структура) - записывается как
выр(арг1, арг2, … , аргn), где аргументы сами являются выражениями.
Структуры Пролога аналогичны записям Паскаля и структурам языка С. Структуры – это составной тип данных, конструируемый программистом. Структуры служат для представления данных об объектах, аргументами структур могут быть как атомы, так и объекты. Структуру можно назвать составным термом. Структура, рассмотренная ниже, содержит информацию об аудиторном занятии:
занятие(преподаватель(кафедра, ФИО), группа(факультет, индекс),
проведение(время, аудитория), вид_занятия)
Объект занятие, представленный такой структурой, называется составным объектом. Термы преподаватель, группа, проведение являются функторами, т.е. предикатами, вставленными внутрь другого предиката. Пролог позволяет объявлять составные объекты в разделе domains. Если структура содержит объекты разных типов, она называется многодоменной структурой. Структура обеспечивает средство сортировки объектов по категориям. Ссылки на доменную структуру осуществляются по имени функтора.
Структуры могут определяться рекурсивно. Рекурсивные структуры могут использоваться для описания различных видов сложных взаимосвязей между термами. Рекурсивная структура в качестве аргумента содержит описание того же домена, к которому принадлежит сама. Примером рекурсивной структуры является структура для описания двоичного дерева.
Приложение б
Краткие сведения о графах и деревьях
В настоящее время теория графов применяется для решения транспортных задач, составления расписания, распределения потоков, представления знаний, выполнения логических выводов и т.д..
Графом называется графическое отображение поименованных точек (вершин) и соединяющих их линий. Соединительные линии без указания направления называются ребрами (рис. П7Б.1). Линии могут быть направленными и иметь стрелку на одном конце, они называются дугами. Граф с дугами называется ориентированным (рис. П7Б.2). Как ребра, так и дуги могут иметь числовую характеристику (вес или стоимость). Такой граф называют нагруженным (рис. П7Б.2).
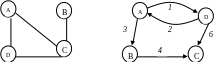
Рисунок П7Б.1 – Неорентированный Рисунок П7Б.2 – Ориентированный
граф граф
Граф задается непустым множеством вершин и непустым множеством ребер (дуг).
В Прологе графы можно представить несколькими способами.
Первый способ – каждое ребро записывается в виде одного факта. Например, графы, изображенные на рис. П7Б.1 и рис П7Б.2 можно представить так:
граф(“A”,”D”).
Продолжение прил. 7Б
граф(“D”,”C”).
. . . . . . . . . . . . . . . .
ор_граф(“A”,”B”,3).
ор_граф(“A”,”D”,1).
ор_граф(“D”,”A”,2).
Другой способ – представление графа в виде одного объекта. В этом случае грая описывается в виде списка вершин и списка ребер. Для наших примеров это может выглядеть так:
Граф1=([“А”,”B”,”C”,”D”],
[ребро(“A”,”D”),ребро(“A”,”C”),ребро(“D”,”C”),ребро(“B”,”C”)])
Граф2=([“А”,”B”,”C”,”D”], [дуга(“A”,”D”,1),дуга(“D”,”А”,2),
дуга(“A”,”В”,3),дуга(”C”,“D”,6),дуга(“B”,”C”,4)])
Еще один способ – представить связи каждой вершины, например:
Граф1=(связь1(“A”,[“D”,”C”]),связь1(“D”,[“C”]),связь1(“C”,[“B”]))
Граф2=(связь2(“A”,[[“D”,1],[”B”,3]]),связь2(“D”,[[“A”,2]]),
связь2(“C”,[[“D”,6]]), связь2(“B”,[[”C”,4)]]))
Выбор способа представления графа зависит от решаемой задачи и операций над графом. Типичные операции – нахождение путей между двумя вершинами, а также подграфа, обладающего определенными свойствами.
Путь – это список последовательно связанных вершин от начальной до целевой. Цикл – это путь, в котором начальная вершина равна целевой. Ациклический путь не содержит циклов, т.е. в нем каждая вершина входит в список только один раз.
Деревом называется граф, не содержащий циклов. Для каждой пары вершин дерева существует только один путь (рис. П7Б.3).
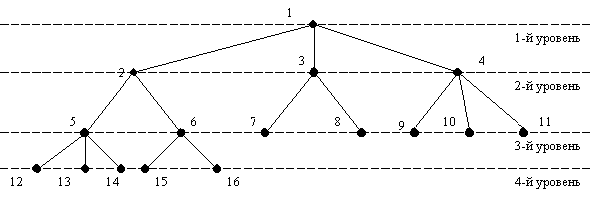
Рисунок П7Б.3 – Дерево
Вершина 1 называется корнем дерева, вершины 12–16 – листьями. Наибольшее количество уровней между корневой и листьевыми вершинами называется высотой дерева. Дерево состоит из ветвей (поддеревьев).
Одним из видов дерева является двоичное дерево. Двоичное дерево либо пусто, либо состоит из следующих эелементов:
корень дерева;
левая ветвь (поддерево);
правая ветвь(поддерево).
Корень может быть любой вершиной, а поддеревья сами должны быть двоичными деревьями.
Для представления двоичных деревьев в Прологе существует ряд способов. Рассмотрим один из них. Введем понятие пустого дерева – nil (это обозначение может быть любым). Кроме этого, разработаем функтор (специальную структуру) для построения непустого дерева из трех компонент (корня и двух ветвей):
tree = nil; %Символ пустого дерева
tr(tree,i,tree) %Структура для непустого дерева
%tr(Левая_ветвь,корень,правая_ветвь)
Приведем пример двоичного дерева и представления его с помощью такой структуры (рис. П7Б.4).
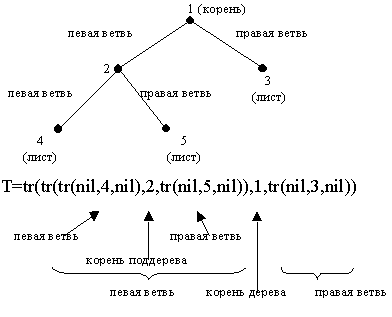
Рисунок П7Б.4 – Двоичное дерево и его представление на Прологе
%Выполняет построение двоичного дерева, вершины которого поименованы целыми %числами
domains i=integer
tree = nil; %Символ пустого дерева
tr(tree,i,tree) %Структура для непустого дерева
%tr(Левая_ветвь,корень,правая_ветвь)
predicates
der1(i,tree) %Сроит первичное (начальное) дерево,
%начиная от указанного корня
der(tree,tree) %Достраивает ветвь - первый параметр входной,
%второй - выходной
der2(tree,tree) %Строит дерево полностью - первый параметр входной,
%второй - выходной
database
f(i,i,i) %Дерево хранится в виде фактов (базы данных):
%f(вершина_слева,корень,вершина_справа)
clauses
f(2,1,3). f(4,2,5). f(0,6,0). f(6,3,0).
f(0,5,8). f(0,8,0). f(7,4,9).f(0,7,0).
f(10,9,0).f(0,10,0).
%der1 строит первичное (начальное) дерево
der1(X,T1):- %Работает, если левая ветвь пуста
f(0,X,R),
R1=tr(nil,R,nil), %Строится правая ветвь
T=(tr(nil,X,R1)), %Вид построенного начального дерева
der(T,T1). %Вызов предиката для построения оcтальной части дерева
der1(X,T1):- %Работает, если правая ветвь пуста
f(L,X,0),
L1=tr(nil,L,nil), %Строится левая ветвь
T=(tr(L1,X,nil)), %Вид построенного начального дерева
der(T,T1). %Вызов предиката для построения оcтальной части дерева
der1(X,T1):- %Работает, если левая и правая ветви не пусты
f(L,X,R),
L1=tr(nil,L,nil), %Строится правая ветвь
R1=tr(nil,R,nil), %Строится правая ветвь
T=(tr(L1,X,R1)), %Вид построенного начального дерева
der(T,T1). %Вызов предиката для построения оcтальной части дерева
%der2 достраивает ветвь
der2(tr(nil,X,nil),tr(nil,X,nil)):-
retract(f(0,X,0)). %достраивается лист
der2(tr(_,X,nil),L):- %достраивается не-лист
f(A,X,0), %с левой ветвью
L1=tr(nil,A,nil),
L=tr(L1,X,nil),
retract(f(A,X,0)).
der2(tr(nil,X,_),L):- %достраивается не-лист
f(0,X,A), %с правой ветвью
R1=tr(nil,A,nil),
L=tr(nil,X,R1),
retract(f(0,X,A)).
der2(tr(_,X,_),L):- %достраивается не-лист
f(A,X,B), %с обеими ветвями
L1=tr(nil,A,nil),
R1=tr(nil,B,nil),
L2=tr(L1,X,R1),
retract(f(A,X,B)),
der(L2,L).
%строит дерево полностью
der(tr(L,X,R),T):-
der2(L,L1), %строит полностью левую ветвь
der2(R,R1), %строит полностью правую ветвь
der(tr(L1,X,R1),T).
der(X,X).
goal
clearwindow,der1(1,P),nl,
write(P).
СПИСОК ЛИТЕРАТУРЫ
Братко И. Программирование на языке ПРОЛОГ для искусственного интеллекта.- М.:Мир, 1990.
Малпас Д. Реляционный язык Пролог и его применение. – М.: Наука, 1990.
Макаллистер Д. Искусственный интеллект и Пролог на микро-ЭВМ. – М.:Машиностроение, 1990.
Содержание
Предисловие 3
лабораторная работа 1 4
лабораторная работа 2 18
лабораторная работа 3 28
лабораторная работа 4 43
лабораторная работа 5 49
лабораторная работа 6 59
лабораторная работа 7 85
Навчальне видання
ПРОГРАМУВАННЯ У СЕРЕДОВИЩІ Turbo Prolog 2.0. Лабораторний практикум з дисципліни
“Алгоритмічні мови систем штучного інтелекту”
для студентів спеціальності
"Інтелектуальні системи прийняття рішень"
Російською мовою
Укладачі Нікітіна Людмила Олексіївна,
Заволодько Ганна Едвардівна,
Хавіна Інна Петрівна.
Відповідальний за випуск О.А. Серков
Роботу рекомендував до видання В.Д. Дмитрієнко