Задача №7.2

В таблице представлены значения EPS DewCompany за 8 лет.

Год	1	2	3	4	5	6	7	8
EPS (долл.)	3,40	3,24	2,88	3,76	4,36	4,65	3,68	3,00

а) Определите величину ежегодных дивидендов на одну акцию при проведении следующих видов дивидендной политики.

Постоянный коэффициент выплаты дивидендов, равный 50%(1 политика).

Регулярные дивиденды величиной 2 долл.(2 политика)и дополнительные дивиденды, чтобы довести коэффициент выплаты до 50%, если он оказывается ниже.

Стабильные дивиденды, которые время от времени повышаются. В каждом году коэффициент выплаты может находиться в диапазоне от 40% до 60%, но в среднем должен равняться примерно 50%.

б) Какой из видов дивидендной политики на ваш взгляд наиболее предпочтителен.

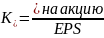
1)

DIV на акцию
N года	1 политика (EPS/2)	2 политика (DIV*2 ≥ EPS, если < то DIV= EPS/2)	3 политика	(для проверки 3 политики подставлять в формулу) (0,4÷0,6)
1	1,7	2	1,59	0,47
2	1,62	2	1,59	0,49
3	1,44	2	1,59	0,55
4	1,88	2	2,13	0,57
5	2,18	2+0,18=2,18	2,13	0,49
6	2,325	2+0,32=2,325	2,13	0,46
7	1,84	2	1,67	0,45
8	1,5	2	1,67	0,56
∑	14,485	15,425	14,5

Формула Стерджесса:

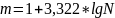
N – количество лет; m- количество групп (когда нельзя самим распределить на группы)

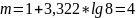
Делим на 3 группы: 1,2,3=>уменьшаются; 4,5,6=>увеличиваются; 7,8=>уменьшаются.

1 гр.: (3,4+3,24+2,88)/3=3,17 =

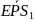
2 гр.: (3,76+4,36+4,65)/3=4,26 =

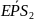
3 гр.: (3,68+3)/2=3,34=

1)

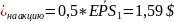
2)

3)

3 политика является оптимальной, т.к. в ней относительно стабилен размер дивидендных выплат.

Управление заемным капиталом

Факторы, оказывающие влияние на стоимость краткосрочного финансирования:

- объявленная (номинальная) процентная ставка;

- компенсационные остатки на депозитном счете;

- комиссионные за предоставление кредита.

Методы уплаты %-ов по краткосрочным займам:

1) на основе полной суммы (% выплачивается по истечении срока займа);

2) на основе дисконтирования (% вычитаются из первоначальной суммы займа).

Задача №8

Сумма займа 10000$, срок 1 год, % ставка 12% годовых. Определить эффективную процентную ставку в случае использования каждого из методов уплаты %.

1) На основе полной суммы (основной. Если не указан метод, то считать по нему)

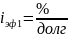
2) На основе дисконтирования

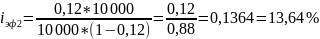
Задача №9

Компания заняла 1 млн. $ под 12% годовых. Банк потребовал наличия остатка на 100 000 $ больше, чем она имеет обычно. Определить эффективную процентную ставку.

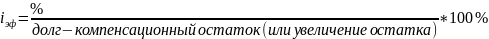
Задача №10

Компании необходимо увеличить оборотный капитал на 4,4 млн. $. Для этого она может воспользоваться одним из двух вариантов финансирования:

1) отказ от скидки за ранние платежи, которые предоставляются на условиях «3/10, нетто 30», и произвести расчет в последний день платежа

2)взять в банке кредит на 5 млн. $ под 15% годовых.

При выборе этой альтернативы фирме придется иметь 12% компенсационного остатка на расчетном счете.

Какую альтернативу следует выбрать, если цена гибкости банковского финансирования не превышает 2% в год.

(«3/10, нетто 30» - если оплатим в течении 10 дней, то скидка 3%. Срок оплаты (обычный) 30 дней)

1) Определим издержки вследствие отказа от скидки:

2)

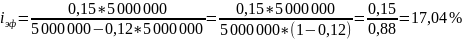
Предприятию лучше всего воспользоваться банковским кредитом, т.к. стоимость его обслуживания меньше издержек по товарному кредиту (17,04<56,44)

Амортизация кредита

Задача №11

Предприниматель взял ссуду в размере 22 000 $ под 12% годовых.

Ссуду необходимо погасить в течение следующих 6 лет в конце каждого года равными долями. Определить величину аннуитета, достаточного для погашения основной суммы долга и процентов. Составить график амортизации ссуды.

Текущая стоимость аннуитета: , i-%-ная ставка, n - срок

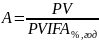
или

А=22000/((1-(1/(1+0,12)⁶))/0,12)=22000/4,111=5351$

Амортизация кредита

n	Aннуитет (А)	%	Погашение основной суммы долга	Остаток основной суммы долга
0				22 000
1	5350,98	2640 0,12*22 000 (%*остаток)	2710,98 5350,98-2640 (А-%)	19 289,02 22 000-2710,98 (Остаток - погашение)
2	5350,98	2314,68	3036,3	16 252,72
3	5350,98	1950,33	3400,65	12 852,07
4	5350,98	1542,25	3808,73	9043,34
5	5350,98	1085,2	4 265,78	4777,56
6	5350,86	573,3	4777,56	0
∑	32 105,76	10 105,76	22 000

Строка №6:

Погашение основной суммы долга = остаток основной суммы долга стр. 5

А = Погашение основной суммы долга + %