1.2. Решение задач линейного программирования симплекс-методом

Ранее рассматривался геометрический метод решения задачи линейного программирования, где число ограничений на 2 меньше числа переменных: n-m = 2. Если же n-m > 2, то для нахождения решения в общем случае используются вычислительные методы, в частности симплекс метод, который является наиболее универсальным. Этот метод позволяет переходить от одного допустимого базисного решения к другому с непрерывным увеличением значений целевой функции. Таким образом, находится оптимальное решение задачи за конечное число шагов или же устанавливается, что задача не имеет решения.

Сведение задачи линейного программирования к каноническому виду.

Для применения симплекс-метода сначала необходимо преобразовать исходную задачу к ее каноническому виду. Рассмотрим общей случай задачи линейного программирования:

Если все ограничения имеют форму строгих равенств с положительной правой частью, целевая функция стремится к максимуму и выполнено условие неотрицательности переменных, то такая форма записи называется канонической:

Для приведения задачи к каноническому виду сформулируем правила перехода:

1. Если исходная целевая функция , то можно умножить ее на -1 и перейти к рассмотрению новой целевой функции: .

2. Любое неравенство также можно умножить на -1 и получить неравенство с другим знаком:

.

3.Чтобы перейти от ограничений-неравенств к ограничениям в форме равенств необходимо ввести дополнительные переменные и в зависимости от знака неравенства переписать:

, если или

, если , .

Например, после соответствующего преобразования задача (1) примет вид:

Утверждается, что всякому неотрицательному решению системы неравенств задачи (1) соответствует решение системы уравнений (3), причем все дополнительные переменные также неотрицательны.

Пример. Привести следующую задачу к каноническому виду:

Так как целевая функция минимизируется, то умножим ее на -1 и перейдем к функции максимизации:

Преобразуем первое ограничение-неравенство путем добавления неотрицательной переменной :

Умножим второе ограничение на -1, чтобы получить положительную правую часть:

Вычтем неотрицательную переменную из третьего неравенства, получим:

В результате исходную задачу свели к каноническому виду:

Преобразование Жордана-Гаусса.

Одна из операций, лежащих в основе алгоритма симплекс-метода, является преобразование Жордана-Гаусса. Рассмотрим ее более подробно.

Пусть задача линейного программирования уже приведена к каноническому виду. Будем рассматривать ее матричную запись:

где , .

Дополнительно, матрицу можно также представить в виде , где - вектора, составленные из соответствующих коэффициентов при :

- расширенная матрица, . Будем обозначать матрицу после k-ой итерации. Далее рассмотрим алгоритм одной итерации преобразования матрицы :

Алгоритм:

1. В матрице выбирают ненулевой элемент (кроме элементов правого столбца). Этот элемент называется направляющим. Строка и столбец, содержащие направляющий элемент – направляющие.

2. Все элементы направляющей строки делятся на направляющий элемент (для определенности пусть это будет ):

…	/	…	/

3. Из каждого элемента (кроме направляющей строки и направляющего столбца) вычитают произведение элементов, расположенных на соответствующем направляющем столбце и преобразованной направляющей строке:

		…
/	…	/

	0
	1
	0

4. Все элементы направляющего столбца, кроме направляющего элемента, становятся равными нулю:

5. После произведенных преобразований новую получившуюся матрицу обозначают .

Пример. Произвести одну итерацию преобразования Жордана-Гаусса для задачи, имеющей следующую систему ограничений:

Соответствующая расширенная матрица имеет вид:

В качестве направляющего элемента выберем . Соответственно, направляющими будут вторая строка и второй столбец. Разделим вторую строку на . Затем преобразуем все оставшиеся элементы матрицы:

Например, чтобы получить новый элемент надо из старого вычесть произведение элементов (элементы соответствующего направляющего столбца и строки): .

В итоге получили:

Алгоритм табличного симплексного метода.

Пусть задача приведена к каноническому виду, и ее матрица ограничений может быть представлена (аналогично (3)) как:

где

Вектора образуют единичную подматрицу размерности . Очевидно, что каждая из переменных входит в соответствующее одно уравнение ограничения с коэффициентом 1 и в других уравнениях его больше нет. Такие переменные как называются базисными, а вся их совокупность (в количестве m штук, равному числу ограничений) – базисом. Остальные переменные называются небазисными или свободными. Неотрицательные решения системы (4) называются допустимыми решениями.

Для решения задачи симплекс-методом составляется таблица специального вида, в которую входят базисные переменные. Алгоритм заключается в переходе от одной таблицы к другой с использованием разных базисных переменных, причем значения целевой функции будут непрерывно увеличиваться (по крайней мере, не уменьшаться). В результате должны получить такой базис, при котором целевая функция максимальна.

Алгоритм симплекс-метода.

1.Привести задачу к каноническому виду, если необходимо. Далее составляется и заполняется следующая таблица с допустимым единичным базисом:

C			c1	c2	…	cj	…	cn
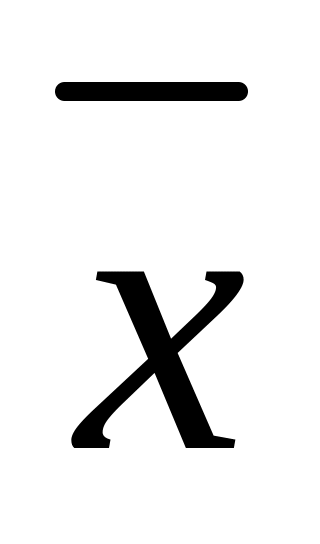
	Bx		A1	A2	…	Aj	…	An	Θ
c1	x1	a10	A11	a12	…	a1j	…	a1n	Θ1
c2	x2	a20	A21	a22	…	a2j	…	a2n	Θ2
…	…	…	…	…	…	…	…	…	…
ci	xi	ai0	ai1	ai2	…	ai j	…	ai n	Θi
…	…	…	…	…	…	…	…	…	…
cm	xm	am0	am1	am2	…	am j	…	am n	Θm
		Δ	Δ1	Δ2	…	Δj	…	Δn

Здесь - исходная базисная точка, в качестве которой первоначально берется вектор . Столбцы векторов заполняются соответствующими значениями коэффициентов системы ограничений. В столбце B_x записываются названия базисных переменных на данной итерации. Столбец C заполняется соответствующими коэффициентами целевой функции, отвечающими столбцу B_x. В строке С выписываются коэффициенты целевой функции.

2. Последняя строка таблицы – индексная. Она служит для получения оценок и последующего выбора направляющего столбца, ячейка Δ – значение целевой функции на данной итерации. Все Δ_j вычисляются по формуле:

где I – множество индексов базисных переменных, J – множество индексов небазисных переменных, . Т.е. каждая получается в результате суммирования попарных произведений элементов столбцов С и A_k, и вычитания из этой суммы значения (расположенного в самом верху столбца A_k ); если же индекс k совпал с индексом одного из базисных векторов, то . Ячейка Δ считается как сумма попарных произведений элементов столбцов С и :

3. В качестве направляющего столбца берут тот, у которого одновременно (обычно это столбец с , но не обязательно) и найдется хоть один положительный элемент . Если выбрать направляющий столбец не удается, то выполнение алгоритма закончено и получен ответ. Возможны следующие варианты:

а) В каждом столбце все : целевая функция неограниченна в области допустимых решений.

б) Все и для всех номеров : : получено единственное оптимальное решение задачи с координатами:

значение целевой функции равно Δ.

в) Все и найдется хоть один номер : : получено оптимальное решение , в задаче бесконечно много решений.

4. Столбец Θ служит для получения оценок и последующего выбора направляющей строки. Все Θ_i считаются по формуле:

где k – индекс выбранного направляющего столбца. Если , то ставят прочерк. Т.е. каждая оценка Θ_i есть отношение элементов столбца к неотрицательным элементам направляющего столбца A_k.

5. В качестве направляющей строки выбирают ту, у которой Θ_i минимально: .

Если таких минимальных элементов Θ_i получилось несколько, то возможен вариант зацикливания (возврат на одну из старых таблиц, такие задачи называются вырожденными). Чтобы его избежать надо взять другой разрешающий столбец (если есть такая возможность).

6. Производят одну итерацию преобразования Жордана - Гаусса с выбранным направляющим элементом ( для расширенной матрицы А_р = [ , ]). Заполняют новую таблицу (продолжают старую), куда заносятся новые значения А_р. В столбце B_x заменяют название на (переход на новую базисную переменную), и в столбце С заменяют на .

7. Перейти в пункт 2.

Пример 1. Решить задачу симплекс методом:

Так как задача не приведена к каноническому виду, то преобразуем ее, добавив дополнительные переменные , , :

Составим и заполним следующую таблицу, где в качестве базиса выберем новые дополнительные переменные:

C			1	-1	-1	5	0	0	0
	Bx		A1	A2	A3	A4	A5	A6	A7	Θ
0		2	-1	2	-1	1	1	0	0	2
0		12	2	1	1	-2	0	1	0	-
0		6	2	-1	4	2	0	0	1	3
	Δ	0	-1	1	1	-5	0	0	0

Посчитаем индексную строку, получили две отрицательные оценки: и . Выберем в качестве направляющего столбца A₄, т.к. оценка этого столбца меньше. После подсчета оценок в столбце Θ ( ), выбираем наименьшую со значением 2. Значит направляющая строка – первая. Составим новую таблицу: в столбце B_x вместо запишем с соответствующим значением коэффициента в столбце С. Проделаем одну итерацию преобразования Жордана – Гаусса. Получим:

C			1	-1	-1	5	0	0	0
	Bx		A1	A2	A3	A4	A5	A6	A7	Θ
5		2	-1	2	-1	1	1	0	0	-
0		16	0	5	-1	0	2	1	0	-
0		2	4	-5	6	0	-2	0	1	0.5
	Δ	10	-6	11	-4	0	5	0	0

После подсчета индексной строки выберем в качестве направляющего столбца A₁ и направляющую строку - третью. Заметим, что значение целевой функции увеличилось. Составим новую таблицу, предварительно заменив на в столбце B_x и 0 на 1 в столбце C. Проделаем еще одну итерацию преобразования Жордана – Гаусса. Получим:

C			1	-1	-1	5	0	0	0
	Bx		A1	A2	A3	A4	A5	A6	A7	Θ
5		2.5	0	0.75	0.5	1	0.5	0	0.25
0		16	0	5	-1	0	2	1	0
1		0.5	1	-1.25	1.5	0	-0.5	0	0.25
	Δ	13	0	3.5	5	0	2	0	1.5

Подсчитаем индексную строку. Т.к. все и на небазисных переменных все , то получено единственное оптимальное решение: со значением целевой функции 13.

Пример 2. Решить задачу симплекс методом:

Приведем задачу к каноническому виду, умножив целевую функцию и первое неравенство на -1. Затем добавим дополнительные переменные , , :

Составим таблицу:

C			-2	-4	1	1	0	0	0
	Bx		A1	A2	A3	A4	A5	A6	A7	Θ
0		16	-1	2	1	-2	1	0	0	16
0		8	1	1	-1	2	0	1	0	-
0		12	4	-1	1	1	0	0	1	12
	Δ	0	2	4	-1	-1	0	0	0

Заполним индексную строку. Направляющий столбец выберем A₃ (т.к. его оценка Δ отрицательна), направляющая строка – третья (минимальная оценка - Θ=12). Сделаем преобразование Жордана-Гаусса и запишем результат в новую таблицу, изменив информацию в столбцах B_x и С ( меняем на ):

C			-2	-4	1	1	0	0	0
	Bx		A1	A2	A3	A4	A5	A6	A7	Θ
0		4	-5	3	0	-3	1	0	-1
0		20	5	0	0	3	0	1	1
1		12	4	-1	1	1	0	0	1
	Δ	12	6	3	0	0	0	0	1

индексную строку. Получили все оценки Δ положительными, однако оценка Δ₄ строго равна 0, значит получено оптимальное решение , задача имеет бесконечно много решений.

М-метод решения задачи линейного программирования.

При решении задач симплекс-методом всегда необходимо иметь полный начальный базис (либо такие переменные даны сразу из условия, либо это дополнительные переменные). Однако если задача задана в произвольной форме, где информация о начальном базисе отсутствует или же базисных переменных не хватает до полного базиса, то симплекс метод применить не удастся. Рассмотрим, например, случай противоположных неравенств:

где после приведения условий к равенствам, получим следующую систему уравнений:

Очевидно, что дополнительные переменные нельзя использовать в качестве начального базиса, т.к. они имеют коэффициент -1.

В таких случаях составляют вспомогательную М-задачу, цель которой – получение полного начального базиса. Если удастся найти оптимальное решение М-задачи, то можно получить и решение исходной задачи.

Главная идея метода – добавление в ограничения-равенства (где это необходимо) искусственных положительных переменных. Также эти переменные добавляются в целевую функцию с достаточно большим коэффициентом М (точное его значение находить не нужно):

знак М выбирается исходя из условия оптимизации: если , то берут –М , если же - берут +М.

Для дальнейшего решения задачи теперь можно применить симплекс-метод. Однако необходимо как можно быстрее избавиться от новых искусственных базисных переменных . Если же удастся показать, что это невозможно, то задача не имеет решения из-за несовместности ограничений.

Заметим, что при решении задачи симплекс-методом в индексной строке появятся значения Δ, выраженные через М линейно: . Очевидно, что при выборе нового базисного столбца важно учитывать лишь значение множителя .

Если на какой-то итерации из базиса выводится искусственная переменная, то в следующей таблице соответствующий ей столбец можно не заполнять (вычеркнуть), он больше не потребуется в дальнейших вычислениях.

Задания для самостоятельного выполнения

Используя геометрическую интерпретацию задачи линейного программирования найдите решение задачи:

;

при ограничениях

Значения коэффициентов A, B, C, D, E, F, G, K, L, M приведены в табл. 1.

Таблица 1

Номер варианта		С1	С2	С3	С4	bi
		ai1	ai2	ai3	ai4
1	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	5	3	2	<120
	3 ограничение	3	5	10	15	<100
2	Целевая функция	4	33/7	9	10
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	5	3	2	<120
	3 ограничение	3	5	10	15	<100
3	Целевая функция	5	5	9	11
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	5	3	2	<120
	3 ограничение	3	5	10	15	<100
4	Целевая функция	5	33/7	9	10
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	5	3	2	<120
	3 ограничение	3	5	10	15	<100
5	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	5	3	2	<140
	3 ограничение	3	5	10	15	<100
6	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	5	3	2	<60
	3 ограничение	3	5	10	15	<100
7	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<12
	2 ограничение	7	5	3	2	<120
	3 ограничение	3	5	10	15	<100
8	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<10
	2 ограничение	7	5	3	2	<120
	3 ограничение	3	5	10	15	<100
9	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<20
	2 ограничение	7	5	3	2	<120
	3 ограничение	3	5	10	15	<100
10	Целевая функция	5	5	9	11
	1 ограничение	1	1	1	1	<20
	2 ограничение	7	5	3	2	<120
	3 ограничение	3	5	10	15	<100
11	Целевая функция	4	5	9	11
	1 ограничение	2	2	2	2	<30
	2 ограничение	7	5	3	2	<120
	3 ограничение	3	5	10	15	<100
12	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	5	3	2	<120
	3 ограничение	3	10	10	15	<100
13	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	5	3	2	<120
	3 ограничение	3	5	10	20	<100
14	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	4	3	2	<120
	3 ограничение	3	5	10	15	<100
15	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	5	3	1	<120
	3 ограничение	3	5	10	15	<100
16	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<15
	2 ограничение	10	5	3	2	<120
	3 ограничение	3	5	10	15	<100
17	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	5	6	2	<120
	3 ограничение	3	5	10	15	<100
18	Целевая функция	40	5	9	11
	1 ограничение	10	1	1	1	<15
	2 ограничение	70	5	3	2	<120
	3 ограничение	30	5	10	15	<100
19	Целевая функция	4	20	9	11
	1 ограничение	1	4	1	1	<15
	2 ограничение	7	20	3	2	<120
	3 ограничение	3	20	10	15	<100
20	Целевая функция	4	5	90	11
	1 ограничение	1	1	10	1	<15
	2 ограничение	7	5	30	2	<120
	3 ограничение	3	5	100	15	<100
21	Целевая функция	15	6	9	2
	1 ограничение	2	1	5	0.6	<10
	2 ограничение	3	1	3	0.25	<12
	3 ограничение	7	0	0	1	<35
22	Целевая функция	60	26	15	4.75
	1 ограничение	20	9	6	1	<20
	2 ограничение	10	4	2	1	<10
	3 ограничение	0	0	0	0	0
23	Целевая функция	8	10	18	22
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	4	3	2	<120
	3 ограничение	3	5	10	15	<100
24	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<15
	2 ограничение	14	8	6	4	<120
	3 ограничение	3	5	10	15	<100
25	Целевая функция	4	5	9	11
	1 ограничение	1	1	1	1	<15
	2 ограничение	7	4	3	2	<120
	3 ограничение	6	10	20	30	<100