I. Задачи линейного программирования

Задачи управления и планирования обычно сводятся к выбору некоторой системы параметров и некоторой системы функций. Эти параметры и функции называют характеристиками управления. Чтобы иметь основание отдавать предпочтение тем или иным значениям параметров планирования и тем или иным управляющим функциям, необходимо, прежде всего, чётко определить два обстоятельства. Во-первых, следует сформулировать и выразить через искомые характеристики показатель качества – некий критерий функционирования данной модели, определяющий соответствие разрабатываемых устройств и планов цели, ради которой эта разработка ведётся. Во-вторых, необходимо выяснить условия работы системы и вытекающие отсюда ограничения, которым должны удовлетворять искомые характеристики.

В общем виде математическая постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения целевой функции f(x₁, x₂, …,x_n) при условиях g_i (x₁, x₂, …, x_n) ≤ b_i (i=1,m) , где f и g_i – заданные функции, а b_i – некоторые действительные числа.

Такая задача получила название задачи математического программирования.

При этом функциональная зависимость, характеризующая качество функционирования системы, называется целевой функцией:

п ри таких ограничениях:

Условия, наложенные на параметры системы, называются ограничениями задачи. Ограничения могут задаваться в виде уравнений и неравенств.

При решении конкретной задачи приходится конкретизировать функциональные зависимости, которые используются для описания функционирования системы. В зависимости от вида используемых функций выделяют: задачи линейного программирования и задачи нелинейного программирования.

1.1.Графическое решение задач линейного программирования

Довольно часто во многих областях практики встречаются задачи оптимизации решений, для которых характерны следующие черты:

- показатель эффективности W представляет собой линейную функцию от элементов решения x₁, x₂, …;

- на решение накладывается ряд ограничительных условий в виде равенств или неравенств.

Такие задачи принять называть задачами линейного программирования.

Несмотря на требование линейности функций и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи и прочие.

Общая постановка задачи.

Пусть имеется ряд переменных:

.

Требуется найти такие значения этих переменных, которые бы максимизировали (минимизировали) функцию:

удовлетворяли системе линейных ограничений:

и, кроме того, выполнялось:

где - заданные коэффициенты.

Для удобства используется следующая более короткая запись:

Заметим, что система ограничений (2) может содержать как неравенства ( ), так и равенства.

Оптимизируемая линейная функция L называется целевой функцией, а её оптимальное значение обозначают L^*. Случай, когда функцию L надо минимизировать, легко сводится к предыдущему, если, изменив знак рассмотреть вместо нее функцию:

Допустимым решением задачи называется любая совокупность переменных , удовлетворяющая условиям (2) и (3). Объединение всех таких решений образует допустимое множество решений R.

Оптимальным решением будем называть то из допустимых решений, при котором целевая функция обращается в максимум (минимум).

Графический метод решения задачи.

Если общее количество неизвестных переменных то такую задачу легко можно решить графическим методом. Будем рассматривать задачу следующего вида:

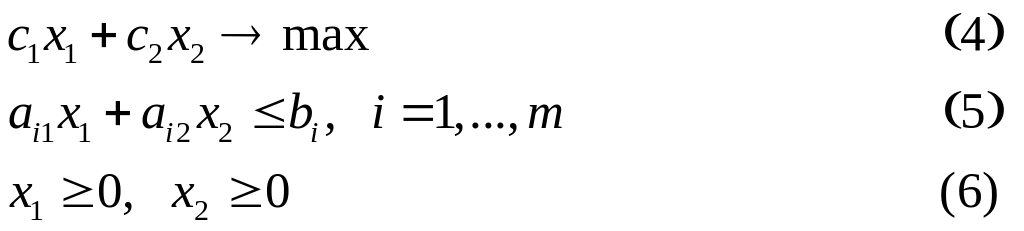
Для отыскания ее оптимального решения необходимо выполнить следующую последовательность действий:

1. Построить допустимое множество R.

Очевидно, что каждое ограничение вида (5) и (6) определяет некоторую полуплоскость в случае неравенства и прямую в случае равенства. Соответственно, допустимое множество решений задачи есть пересечение всех этих полуплоскостей и прямых.

Пусть ограничение имеет вид:

.

Чтобы изобразить соответствующую полуплоскость необходимо провести прямую и далее подставив точку, не лежащую на данной прямой проверить, будет ли выполняться (7). Если да, то выбрать полуплоскость, содержащую данную точку, иначе – выбрать противоположную полуплоскость.

При построении допустимого множества R могут возникнуть следующие ситуации:

- R пусто и, следовательно, задача решений не имеет;

- R является выпуклым многогранником (ограничено);

- R является многогранным неограниченным.

2. Графическое отыскание решения.

а) Выбрать два произвольных числа d₁ и d₂, пусть .

б) Построить линии уровня целевой функции, соответствующие выбранным константам: . Зафиксировать направление увеличения значений целевой функции от прямой с правой частью d₂ к прямой с правой частью d₁.

в) Передвигать прямую параллельно себе по допустимому множеству в обозначенном направлении пока она не выйдет на границу R. Получить максимальное значение d^*. Возможны следующие варианты:

- прямая и допустимое множество решений R имеют одну общую точку (которая является крайней);

- получилось целое множество общих точек (т.е. прямая совпадает с одной из граней многогранника R);

- прямая не выходит на границу допустимого множества R, сколько бы ее не перемещали. Эта ситуация возникает когда целевая функция оказывается неограниченной из-за неограниченности множества R.

3. Выписать ответ.

Чтобы найти точные координаты оптимальной точки (в случае единственного решения) и численное значение d^* необходимо выписать соответствующие уравнения прямых (граней многогранника R) и решить полученную систему уравнений.

В случае бесчисленного множества решений на графике выделяется целый отрезок прямой, все точки которого обеспечивают максимальное значение целевой функции. Крайние точки этого отрезка - пересечение соответствующих граней многогранника R, их координаты находятся также из соответствующих систем уравнений прямых.

При решении задач линейного программирования были подмечены следующие закономерности:

- оптимальное решение задачи, если оно существует, не может лежать внутри области допустимых решений, а только на ее границе;

- оптимальное решение всегда достигается в одной из вершин многогранника R (если оно достигается на целой стороне, то оно же достигается и в каждой из вершин, через которые проходит эта сторона);

- для того, чтобы найти оптимальное решение, достаточно перебрать все вершины допустимого множества и выбрать из них ту, где целевая функция максимальна.

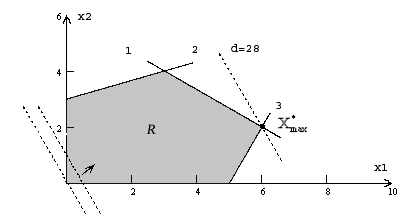
Пример 1. Решить графически следующую задачу:

Согласно шагу 1 строим область допустимых решений. Получился выпуклый многоугольник R. Далее строим линии уровня целевой функции:

Затем, перемещая прямую параллельно себе в нужном направлении, пока она будет сохранять общие точки с множеством R, найдем, что в крайне возможном положении она пройдет через точку . Для нахождения координат этой точки составим и решим систему уравнений граничных прямых:

В результате получим оптимальное решение с значением целевой функции .

Пример 2.

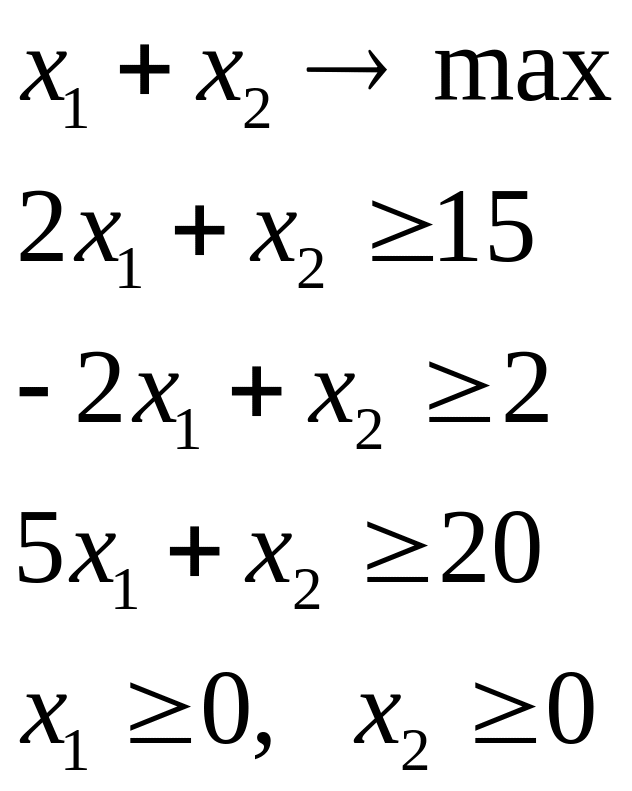
Первый шаг - строим допустимое множество решений. Получается неограниченная многогранная область. На втором шаге, строя и перемещая линию уровня параллельно себе фиксируем нужное направление. Замечаем, что такое перемещение можно производить неограниченно. Значит целевая функция неограниченна сверху и задача неразрешима.

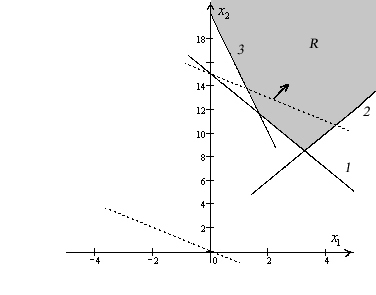
Графический метод можно применить и для задач с любым числом переменных, но только если ограничения представляют собой равенства (2’) и их число на 2 единицы меньше числа переменных, т.е. . Тогда систему (2’) разрешают относительно двух каких-либо переменных (например, x₁ и x₂):

и затем подставляют полученные равенства для в целевую функцию, которая также будет зависеть только от двух переменных.

Пример 3.

Строим множество допустимых решений. Получился выпуклый многоугольник. Строим линии уровня с правой частью d = 3 и d = 5, фиксируем направление возрастания целевой функции. Замечаем, что целевая функция параллельна одной из прямых граничного ограничения и достигает свои максимальные значения на всем отрезке, заключенном между точками и . Координаты точек находятся их соответствующих систем уравнения:

.

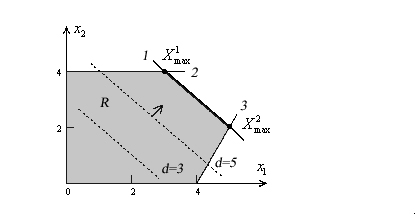
В этом случае оптимальное решение записывается следующим образом:

Таким образом, максимальное значение целевой функции данной задачи - , а любое решение имеет вид:

.

Пример 4.

Область допустимых решений – неограниченный многоугольник. Строим линии уровня с правой частью d = 0 и d = 1, замечем нужное направление. Очевидно, максимальное значение целевая функция достигает на всем луче, полученном пересечением оси ординат и соответствующего граничного условия 1 области R.

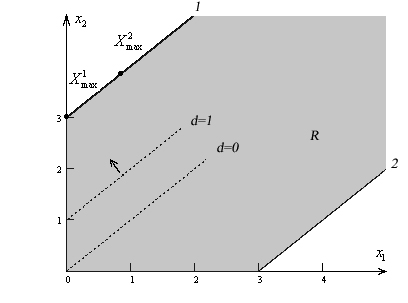
Чтобы выписать решение в общем виде, необходимо взять точку начала луча и еще одну точку, например . Тогда, подставляя и в уравнение луча:

получим решение задачи в общем виде со значением целевой функции :

.

Пример 5. Решить задачу:

Как видно, число ограничений на 2 меньше числа переменных, следовательно, можно использовать графический метод. Решим эту систему относительно и :

Подставим также и в целевую функцию, получим следующую задачу:

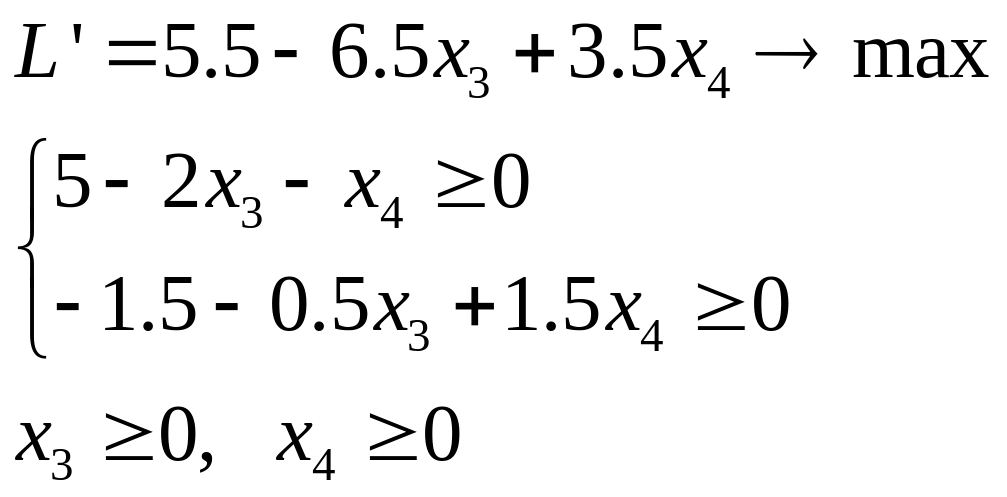
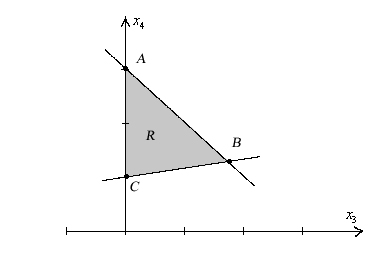
Максимальное значение будет в точке A = (6, 5). Следовательно, и оптимальное решение – точка .

Очевидно, что в случае с тремя переменными графический способ решения довольно затруднителен, а с четырьмя и более переменными вовсе невозможен.

Задания для самостоятельного выполнения

Используя геометрическую интерпретацию задачи линейного программирования найдите решение задачи:

;

.

Значения коэффициентов A, B, C, D, E, F, G, K, L, M приведены в табл. 1.

Таблица 1

Номер варианта	A	B	C	D	E	F	G	H	K	L	M
1	2	2	2	0,5	20	1	1	15	2	0,4	10
2	3	1	4	0,3	24	0,5	5	25	2	2	18
3	4	1	20	7	140	15	10	150	5	20	100
4	5	4	25	8	200	20	11	220	10	25	250
5	6	2	30	9	270	25	12	300	15	30	450
6	7	6	35	10	350	30	13	390	20	35	700
7	8	4	10	10	100	8	12	96	6	14	84
8	9	3	11	11	121	10	13	130	7	16	112
9	10	6	12	12	144	12	14	168	8	18	144
10	11	7	13	13	169	14	16	224	9	20	180
11	12	8	14	14	196	16	18	288	10	22	220
12	13	7	15	15	225	18	20	360	12	24	288
13	14	10	16	16	256	20	22	440	14	26	364
14	15	12	17	17	289	22	24	528	16	28	448
15	16	13	18	18	324	24	26	624	18	30	540
Продолжение табл. 1
Номер варианта	A	B	C	D	E	F	G	H	K	L	M
16	17	14	19	19	361	26	28	728	20	32	640
17	18	13	20	20	400	28	30	840	22	34	748
18	19	14	21	21	441	30	32	960	24	36	864
19	20	17	22	22	484	32	34	1088	26	38	988
20	21	16	23	23	529	34	36	1224	28	40	1120
21	22	14	24	24	576	36	38	1368	30	42	1260
22	23	12	25	25	625	38	40	1520	32	44	1408
23	24	13	26	26	676	40	42	1680	34	46	1564
24	25	14	27	27	729	42	44	1848	36	48	1728
25	26	15	28	28	784	42	46	1932	38	50	1900