Градиентные методы

Если найти градиент функции f(x) в точке х , то антиградиентом будет называться функция - . Антиградиент показывает направление уменьшения функции f(x) . Это свойство послужило основой градиентных методов. Согласно этим методам на k-итерации вычисляют по формуле:

Методы отличаются способом выбора множителя . Если - достаточно мало, то при этом наверняка обеспечивается выполнение неравенства , но число итерацией может быть очень велико. С другой стороны, при больших значениях неравенство может и не выполняться.

Наиболее простой способ выбора - это положить его одинаковым для всех итераций. При этом если неравенство будет нарушаться, то для данной итерации уменьшается до тех пор пока указанное неравенство не будет справедливым.

Пример решения задачи нелинейного программирования методами спуска: методом покоординатного спуска и градиентным методом.

Постановка задачи.

Требуется определить, в каком количестве необходимо выпускать продукцию вида А и вида Б, чтобы полученная прибыль была максимальной. Данные приведены в таблице № 1

Таблица № 1

Продукция	А	Б	Ресурсы
Выпуск кол-во			-
Трудоемкость, чел.-мес.			5
Прибыль, тыс.руб.		2 2	-

Задача может быть записана как стандартная задача нелинейного программирования

Запишем исходную задачу, как задачу минимизации

Решение задачи нелинейного программирования методом покоординатного спуска.

Решим задачу методом покоординатного спуска, принимая за начальное приближение значения .

1). Вычисляется значение целевой функции в этой точке:

f(x₁⁰, x₂⁰)=f(0,5;0,5)=(0,5)² – 4×0,5–2×(0,5)² = 0,25–2–0,5= –2,25.

Проверяем выполнение ограничений задачи:

4×(0,5)² +3×(0,5)² ≤ 5;

1,75≤ 5.

Ограничение задачи выполняется, значит, переходим к покоординатному спуску.

2).Согласно этому методу, направление спуска выбирается параллельным координатным осям. Сначала производится спуск вдоль оси ОХ , затем - вдоль оси ОХ и т.д.

Длина шага вдоль этого направления:

α = 0,1.

Cледующая точка получается в результате вычислений по формуле (3.1):

x₁¹=x₁⁰+ α;

x₁¹=0,5 +0,1=0,6.

Так как спуск осуществляем вдоль оси ОХ₁, вторая координата остаётся без изменений.

Вычисляется значение целевой функции в этой точке:

f(x₁¹, x₂⁰)=f(0,6;0,5)=(0,6)² – 4×0,6–2×(0,5)² = 0,36–2,4–0,5= –2, 54.

Проверяем выполнение ограничений задачи:

4×(0,6)² +3×(0,5)² ≤ 5;

2,19 ≤ 5.

Сравниваем значения целевой функции f(x₁¹, x₂⁰) и f(x₁⁰, x₂⁰):

–2, 54<-2,25.

3).Осуществляем спуск вдоль оси ОХ₂:

х₂¹=x₂⁰+ α;

x₂¹=0,5 +0,1=0,6.

Так как спуск осуществляем вдоль оси ОХ₂, другая координата остаётся без изменений.

Вычисляется значение целевой функции в этой точке:

f(x₁¹, x₂¹)=f(0,6;0,6)=(0,6)² – 4×0,6–2×(0,6)² = 0,36–2,4–0,72 = –2,76.

Проверяем выполнение ограничений задачи:

4×(0,6)² +3×(0,6)² ≤ 5;

2,52 ≤ 5.

Сравниваем значения целевой функции f(x₁¹, x₂¹) и f(x₁¹, x₂⁰):

–2,76<–2, 54.

4).Осуществляем спуск вдоль оси ОХ₁:

x₁²=0,6 +0,1=0,7;

x₂¹=0,6.

Вычисляется значение целевой функции в этой точке:

f(x₁², x₂¹)=f(0,7;0,6)=(0,7)² – 4×0,7–2×(0,6)² = 0,49–2,8–0,72 = –3,03.

Проверяем выполнение ограничений задачи:

4×(0,7)² +3×(0,6)² ≤ 5;

3,04≤ 5.

Сравниваем значения целевой функции f(x₁², x₂¹) и f(x₁¹, x₂¹):

–3,03<–2,76.

5).Осуществляем спуск вдоль оси ОХ₂:

x₂²=0,6 +0,1=0,7;

x₁²=0,7.

Вычисляется значение целевой функции в этой точке:

f(x₁², x₂²)=f(0,7;0,7)=(0,7)² – 4×0,7–2×(0,7)² = 0,49–2,8–0,98= –3,29.

Проверяем выполнение ограничений задачи:

4×(0,7)² +3×(0,7)² ≤ 5;

3,43≤ 5.

Сравниваем значения целевой функции f(x₁², x₂²) и f(x₁², x₂¹):

–3,29<–3,03.

6).Осуществляем спуск вдоль оси ОХ₁:

x₁³=0,7 +0,1=0,8;

x₂²=0,7.

Вычисляется значение целевой функции в этой точке:

f(x₁³, x₂²)=f(0,8;0,7)=(0,8)² – 4×0,8–2×(0,7)² = 0,64–3,2–0,98 = –3,54.

Проверяем выполнение ограничений задачи:

4×(0,8)² +3×(0,7)² ≤ 5;

4,03≤ 5.

Сравниваем значения целевой функции f(x₁³, x₂²) и f(x₁², x₂²):

–3,54 <–3,29.

7).Осуществляем спуск вдоль оси ОХ₂:

x₂³=0,7 +0,1=0,8;

x₁³=0,8.

Вычисляется значение целевой функции в этой точке:

f(x₁³, x₂³)=f(0,8;0,8)=(0,8)² – 4×0,8–2×(0,8)² = 0,64–3,2–1,28= –3,84.

Проверяем выполнение ограничений задачи:

4×(0,8)² +3×(0,8)² ≤ 5;

4,48≤ 5.

Сравниваем значения целевой функции f(x₁³, x₂³) и f(x₁³, x₂²):

–3,84<–3,54.

8).Осуществляем спуск вдоль оси ОХ₁:

x₁⁴=0,8 +0,1=0,9;

x₂³=0,8.

Вычисляется значение целевой функции в этой точке:

f(x₁⁴, x₂³)=f(0,9;0,8)=(0,9)² – 4×0,9–2×(0,8)² = 0,81–3,6–1,28= –4,07.

Проверяем выполнение ограничений задачи:

4×(0,9)² +3×(0,8)² ≤ 5;

5,16≥ 5.

Ограничение не выполняется, а значит, оптимальное решение будет следующее: x₁³=0,8; x₂³=0,8. Целевая функция при этом решении:

f(x₁³, x₂³)= –3,84.

Результаты вычислений сведены в таблицу № 2.

Таблица № 2

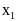
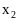
0,5	0,5	-2,25	1,75
0,6	0,5	-2,54	2,19
0,6	0,6	-2,76	2,52
0,7	0,6	-3,03	3,04
0,7	0,7	-3,29	3,43
0,8	0,7	-3,54	4,03
0,8	0,8	-3,84	4,48
0,9	0,8	-4,07	5,16

Полученное решение уточняем градиентным методом.

Решение задачи нелинейного программирования градиентным методом.

1). Начальное приближение значения х₁=0,7; х₂=0,7.

Вычисляется значение целевой функции в этой точке:

f(x₁, x₂)=f(0,7;0,7)=(0,7)² – 4×0,7–2×(0,7)² = 0,49–2,8–0,98= –3,29.

Проверяем выполнение ограничений задачи:

4×(0,7)² +3×(0,7)² ≤ 5;

3,43≤5.

В градиентных методах для направления спуска используется свойство функции, заключающееся в том, что функция убывает в наибольшей степени в направлении антиградиента.

Длина шага вдоль этого направления:

α = 0,01.

Определяем градиент для х₁:

f^’(х₁)=2× х₁–4=2×0,7–4=-2,6

Определяем градиент для х₂:

f^’(х₂)=-4× х₂=-4×0,7=–2,8

2). Осуществляем спуск по формуле:

х₁= х₁- α× f^’(х₁)=0,7 – 0,01×(–2,6)= 0,726.

х₂= х₂- α× f^’(х₂)=0,7-0,01×(–2,8)= 0,728.

Вычисляется значение целевой функции в этой точке:

f(x₁, x₂)=f(0,726;0,728)=(0,726)² – 4×0,726–2×(0,728)² =

=0,527076–2,904–1,059968= –3,436892.

Проверяем выполнение ограничений задачи:

4×(0,726)² +3×(0,728)² ≤ 5;

3,698256≤5.

Определяем градиент для х₁:

f^’(х₁)=2× х₁–4=2×0,726–4=-2,548.

Определяем градиент для х₂:

f^’(х₂)=-4× х₂=-4×0,728=–2,912.

3). Осуществляем спуск по формуле:

х₁= х₁- α× f^’(х₁)= 0,726– 0,01×(–2,548)= 0,75148.

х₂= х₂- α× f^’(х₂)= 0,728 -0,01×(–2, 912)=0,75712.

Вычисляется значение целевой функции в этой точке:

f(x₁, x₂)=f(0,75148; 0,75712)=( 0,75148)² – 4×0,75148–2×(0,75712)² =

=–3,5876591.

Проверяем выполнение ограничений задачи:

4×(0,75148)² +3×(0,75712)² ≤ 5;

3,9785802≤5.

Определяем градиент для х₁:

f^’(х₁)=2× х₁–4=2×0,75148–4=-2,49704.

Определяем градиент для х₂:

f^’(х₂)=-4× х₂=-4×0,75712=–3,02848.

4). Осуществляем спуск по формуле:

х₁= х₁- α× f^’(х₁)= 0,75148– 0,01×(–2, 49704)= 0,7764504.

х₂= х₂- α× f^’(х₂)= 0,75712-0,01×(–3,02848)=0,7874048.

Вычисляется значение целевой функции в этой точке:

f(x₁, x₂)=f(0,7764504; 0,7874048)=

=(0,7764504)² – 4×0,7764504–2×(0,7874048)² = –3,742939.

Проверяем выполнение ограничений задачи:

4×(0,7764504)² +3×(0,7874048)² ≤ 5;

4,2715197≥ 5.

Определяем градиент для х₁:

f^’(х₁)=2× х₁–4=2×0,7764504–4=-2,4470992.

Определяем градиент для х₂:

f^’(х₂)=-4× х₂=-4×0,7874048=–3,1496192.

5). Осуществляем спуск по формуле:

х₁= х₁- α× f^’(х₁)= 0,7764504– 0,01×(–2,4470992)= 0,8009213.

х₂= х₂- α× f^’(х₂)= 0,7874048 -0,01×(–3,1496192)=0,8189009.

Вычисляется значение целевой функции в этой точке:

f(x₁, x₂)=f(0,8009213; 0,8189009)=

=(0,8009213)² – 4×0,8009213–2×(0,8189009)² = –3,9034075.

Проверяем выполнение ограничений задачи:

4×(0,8009213)² +3×(0,8189009)² ≤ 5;

4,5776954≥ 5.

Определяем градиент для х₁:

f^’(х₁)=2× х₁–4=2×0,8009213–4=-2,3981574.

Определяем градиент для х₂:

f^’(х₂)=-4× х₂=-4×0,8189009=–3,2756036.

6). Осуществляем спуск по формуле:

х₁= х₁- α× f^’(х₁)= 0,8009213– 0,01×(–2,3981574)= 0,8336773.

х₂= х₂- α× f^’(х₂)= 0,8189009 -0,01×(–3,2756036)=0,8516569.

Вычисляется значение целевой функции в этой точке:

f(x₁, x₂)=f(0,8336773; 0,8516569)=

=(0,8336773)² – 4×0,8336773–2×(0,8516569)² = –4,0903302.

Проверяем выполнение ограничений задачи:

4×(0,8336773)² +3×(0,8516569)² ≤ 5;

4,9560294 ≥ 5.

Определяем градиент для х₁:

f^’(х₁)=2× х₁–4=2×0,8336773–4=-2,3326454.

Определяем градиент для х₂:

f^’(х₂)=-4× х₂=-4×0,8516569=–3,4066276.

7). Осуществляем спуск по формуле:

х₁= х₁- α× f^’(х₁)= 0,8336773– 0,01×(–2,3326454)= 0,8570037.

х₂= х₂- α× f^’(х₂)= 0,8516569-0,01×(–3,4066276)= 0,8857231.

Вычисляется значение целевой функции в этой точке:

f (x₁, x₂)=f(0,8570037; 0,8857231)=

=(0,8570037)² – 4×0,8570037–2×(0,8857231)² = –4,2625703.

Проверяем выполнение ограничений задачи:

4×(0,8570037)² +3×(0,8857231)² ≤ 5;

5,2913374≥ 5.

Определяем градиент для х₁:

f^’(х₁)=2× х₁–4=2×0,8570037–4=-2,2859926.

Определяем градиент для х₂:

f^’(х₂)=-4× х₂=-4×0,8857231=–3,5428924.

Ограничение не выполняется, а значит, оптимальное решение будет следующее: x₁=0,8336773; x₂=0,8516569. Целевая функция при этом решении:

f(x₁, x₂)= –4,0903302.

Результаты вычислений сведены в таблицу № 3.

Таблица № 3

0,7	0,7	-3,29	3,43	-2,6	-2,8
0,726	0,728	–3,436892	3,698256	-2,548	-2,912
0,75148	0,75712	–3,5876591	3,9785802	-2,49704	–3,02848
0,7764504	0,7874048	–3,742939	4,2715197	-2,4470992	–3,1496192
0,8009213	0,8189009	–3,9034075	4,5776954	-2,3981574	–3,2756036
0,8336773	0,8516569	–4,0903302	4,9560294	-2,3326454	3,4066276
0,8570037	0,8857231	–4,2625703	5,2913374	–2,2859926	–3,5428924