Задача 1.5

Найти удельную энергию связи нуклидов ²Н, ⁶Li, ⁴⁰Ar, ¹⁰⁷Ag, ¹⁵²Dy (Δ = -0,075271 а.е.м.), ²³⁵U и построить график зависимости

Решение

По определению

.

(1.5.1)

Вычисления рекомендуется произвести самостоятельно. Для вычисления ΔW(A,Z) следует воспользоваться формулой (1.3) и данными из табл. 1 Приложений. Должны быть получены следующие результаты:

(²Н) = 2,23 МэВ, (⁶Li) = 5,33 МэВ, (⁴⁰Ar) = 8,60 МэВ, (¹⁰⁷Ag) = 8,55 МэВ, (¹⁵²Dy) = 8,11 МэВ, (²³⁵U) = 7,59 МэВ.

Полученная кривая дает примерные величины удельной энергии связи нуклона в МэВ/нуклон для β-стабильных нуклидов.

Задача 1.6

Определить: а) энергию связи нейтрона и α-частицы в ядре ²¹Ne; б) энергию, необходимую для разделения ядра ¹⁶О на четыре одинаковые частицы.

Решение

а) Устойчивое ядро ²¹Ne образуется при захвате нейтрона ядром ²⁰Ne. Энергия, которая выделяется в этом процессе, численно равна энергии связи нейтрона в ядре ²¹Ne:

ΔWn(21Ne) = [Δn + Δ (20Ne) - Δ (21Ne)]·931,5 = = [0,008655 - 0,007560 + 0,006151] ·931,5 = 6,76 МэВ

Рассуждая подобным же образом, можно считать, что ядро образовалось при слиянии ядер и , а энергия связи α‑частицы в ядре ²¹Ne равна:

ΔWα(21Ne) = [Δα + Δ (17О) - Δ (21Ne)]·931,5 = = [0,002604 – 0,000867 + 0,006151] ·931,5 = 7,34 МэВ

б) При разделении ядра на четыре одинаковых фрагмента образуются ядры с нуклонным составом (4,2), которые являются α-частицами. По общему правилу энергия разделения ядра ¹⁶О на четыре α‑частицы равна

ΔW_4α(¹⁶О) = [4Δ_α - Δ (¹⁶О)]·931,5 =

= [4·0,002604 + 0,005085] ·931,5 = 14,4 МэВ

Задача 1.7

Вычислить энергию связи нейтрона в ядре ¹⁴N, если известно, что энергии связи ядер ¹³N и ¹⁴N равны 94,10 и 104,66 МэВ.

Решение

Энергия связи нейтрона в ядре ¹⁴N равна:

ΔWn(14N) = mn + Mат(13N) – Mат(14N).

(1.7.1)

Воспользуемся формулой (1.2) для выражения масс нуклидов ¹³N и ¹⁴N через энергию связи их ядер:

Mат(13N) = 7mH + (13-7)mn - ΔW(13N),	(1.7.2)
Mат(14N) = 7mH + (14-7)mn - ΔW(14N).	(1.7.3)

Подставив (1.7.2) и (1.7.3) в (1.7.1) получим, что

ΔWn(14N) = ΔW(14N) - ΔW(13N) = 104,66 – 94,10 = 10,56 МэВ.

Задача 1.8

Найти энергию, необходимую для разделения ядра ¹⁶О на α-частицу и ядро ¹²С, если известно, что энергии связи ядер ¹⁶О, ¹²С и ⁴Не равны 127,62; 92,16 и 28,30 МэВ.

Решение

Выкладки, аналогичные тем, которые сделаны в задаче 1.8, приводят к следующему результату:

ΔW_α(¹⁶О) = ΔW(¹⁶О) - ΔW(⁴Не) - ΔW(¹²С) =

=127,62 – 92,16 – 28,30 = 7,16 МэВ.

Задача 1.9

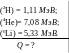О пределить энергию, выделяющуюся при образовании двух α-частиц в результате синтеза ядер ²Н и ⁶Li, если известно, что энергии связи на один нуклон в ядрах ²Н, ⁴Не и ⁶Li равны 1,11; 7,08 и 5,33 МэВ соответственно.

Решение

Запишем схему процесса синтеза:

²Н + ⁶Li → ⁴Не + ⁴Не

По определению, энергия Q, которая освобождается в этом процессе, численно равна разности масс исходной и конечной систем:

Q = Mат(2H) + Mат(6Li) – 2Mат(4He).

(1.9.1)

Используя формулу (1.2) для выражения в (1.9.1) масс атомов через их энергию связи (проделать самостоятельно), получим

Q = 2ΔW(4He) - ΔW (2H) - ΔW(6Li) = = 2·4 (4Не) - 2 (2Н) - 6 (6Li) = = 2·4·7,08 - 2·1,11 - 6·5,33 = 22, 44 МэВ