1.2 Внутренняя энергия

В технической термодинамике внутреннюю энергию обычно рассматривают как сумму двух слагаемых:

- внутренней кинетической энергии — суммарной кинетической энергии всех частиц, образующих систему;

- внутренней потенциальной энергии — потенциальной энергией, обусловленной силами взаимодействия между этими частицами (рис. 1.2).

Рис. 1.2. К определению понятия внутренней энергии

Принято обозначать внутреннюю энергию всей системы U, а отнесённую к единице массы — u . В первом случае она измеряется в Дж (джоулях), во втором — в Дж/кг.

Кинетическая энергия частиц пропорциональна температуре системы, а потенциальная энергия их взаимодействия зависит от расстояния между ними, т. е. от удельного объёма системы. Таким образом, в общем случае

u = u (T, υ) , (1.15)

то есть, внутренняя энергия однозначно определяется двумя основными параметрами состояния, и поэтому является тоже параметром состояния.

Поскольку в идеальном газе отсутствуют силы межмолекулярного взаимодействия, постольку его внутренняя энергия состоит лишь из кинети- ческой энергии составляющих частиц, т. е. она однозначно определяется только температурой газа:

u = u (T) . (1.15а)

1.3. Энтальпия

Энтальпия (теплосодержание, тепловая функция) всей системы обозначается Н и измеряется в джоулях (Дж), а отнесенная к единице массы обозначается h и измеряется в Дж/кг. Как и внутренняя энергия, энтальпия является параметром состояния, т. к. однозначно определяется другими параметрами состояния:

h = u + рυ. (1.16)

Отсюда

dh =du +d (рυ) (1.17)

Умножая обе части равенства (1.16) на массу всей системы m, получим выражение для определения энтальпии всей систёмы:

Н = U +рV,

Энтальпия – функция состояния термодинамической системы равная сумме ее внутренней энергии и произведения давления на объем системы.

1.4. Энтропия

Энтропия — параметр состояния (S), определяемый тем, что его дифференциал (dS) равен отношению бесконечно малого количества теплоты (dQ), участвующего в процессе, к абсолютной температуре, при которой эта теплота подводилась или отводилась:

для всей системы dS = dQ/Т, (1.18)

для 1 кг массы ds = dq/Т. (1.19)

В первом случае размерность Дж/К, а во втором — Дж(кг·К).

Если система адиабатна, т. е. не получает и не отдаёт теплоту (dq=0,

dQ =0) то, как следует из формул (1.18) и (1.19), её энтропия не меняется ds= dS =0. Иначе говоря, энтропия такой системы постоянна (S=const и s=const). В теплотехнических расчётах внутренняя энергия, энтропия и энтальпия принимаются равными нулю при нормальных физических условиях.

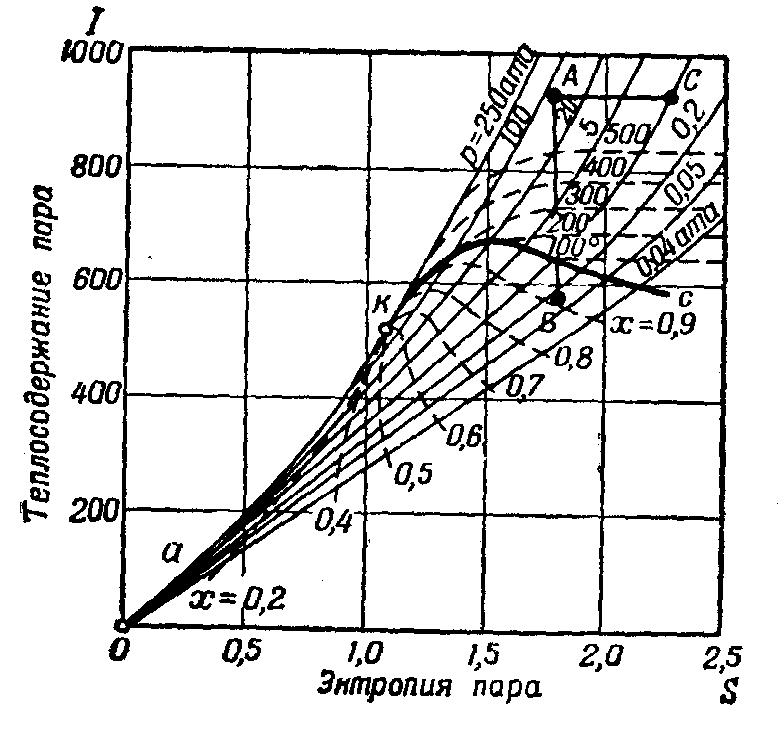
ЭНТРОПИЙНАЯ ДИАГРАММА — диаграмма, у к-рой по горизонтальной оси откладывается энтропия S, а по вертикальной — абсолютная т-ра Т (Т- S -диаграмма) или же теплосодержание I (I- S диаграмма). Э. д. облегчает теплотехнические расчеты. Наиболее часто применяется I- S диаграмма для водяного пара. На диаграмме проведены линии постоянных температур (изотермы), давлений (изобары), удельных объемов и паросодержания. Процесс адиабатического расширения пара (без сообщения и потерь тепла) изображается в I- S диаграмме вертикальной линией (АВ), проведенной из точки, соответствующей начальным параметрам пара, до пересечения с изобарой конечного давления пара. Процесс дросселирования изображается горизонтальной линией АС, проведенной из точки, соответствующей состоянию пара с начальными параметрами, до пересечения с изобарой конечного давления. Путем несложных построений можно найти конечные параметры пара для того или иного процесса

ЛЕКЦИЯ 3

(Сл24…31)