10. Подстановки Эйлера

Интеграл вида можно свести к интегралу от рациональной функции с помощью подстановок Эйлера.

1) Если , то используем 1 подстановку Эйлера

возведя оби части равенства в квадрат, можно найти и .

2) Если , то используем 2 подстановку Эйлера

преобразования аналогичны.

3) Если квадратный трехчлен имеет два действительных корня и , то применяем 3 подстановку Эйлера причем неважно какой корень взять.

Замечание 1.

При использовании 1 и 2 подстановок Эйлера знак «+» или «-» выбирается, исходя из условия так, чтобы полученная рациональная функция максимально упростилась.

Замечание 2.

Прежде чем применить подстановки Эйлера, нужно внимательно посмотреть на интеграл.

Если он имеет вид , то рациональнее решить с помощью выделения полного квадрата (см. стр. 15 ).

Если он имеет вид или , то лучше применить подстановку (см. стр. 9 )

Замечание 3.

На самом деле достаточно использовать только 1 и 3 подстановки Эйлера.

Пример 1.

Пример 2.

Пример 3.

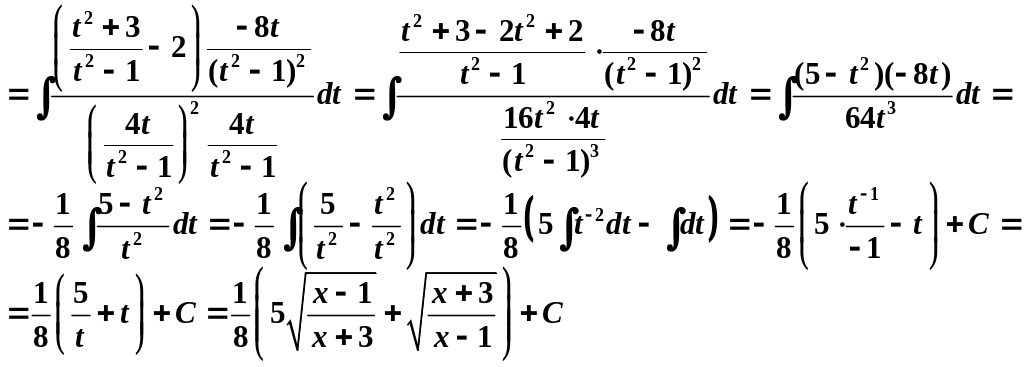
Пример 4.

Пример 5.

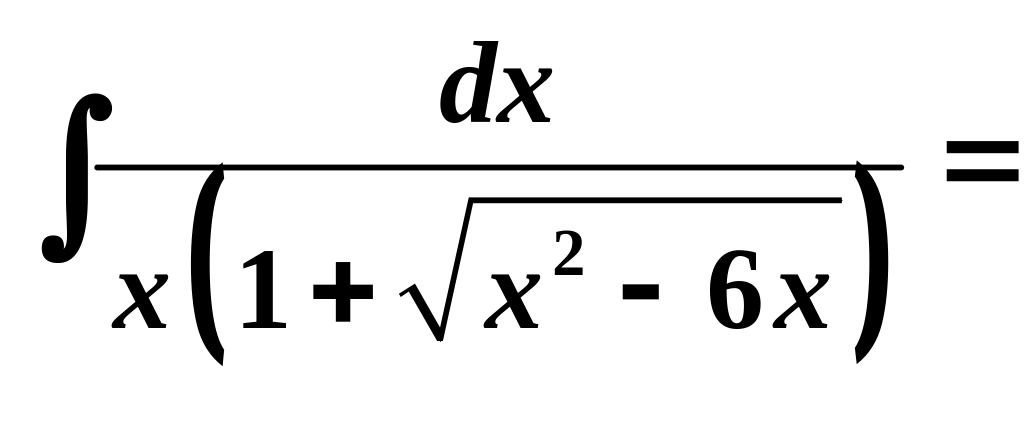
Приложения:

1. Формулы сокращенного умножения.

2. Свойства степеней.

3. Свойства логарифмов.

4. Тригонометрические формулы.

5. Таблица производных.

6. Правила дифференцирования.

7. Таблица дифференциалов.

1.Формулы сокращенного умножения

2. Свойства степеней

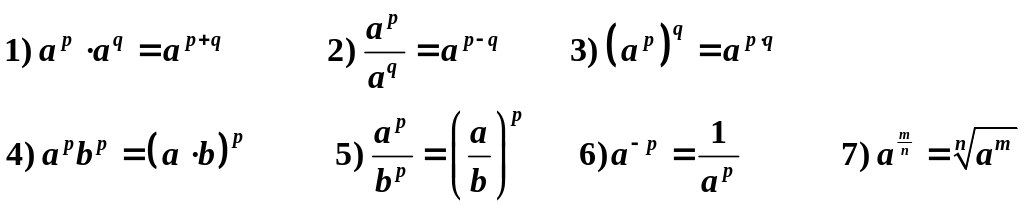
где p, q – рациональные числа, m – целое число, n – натуральное число

3. Свойства логарифмов

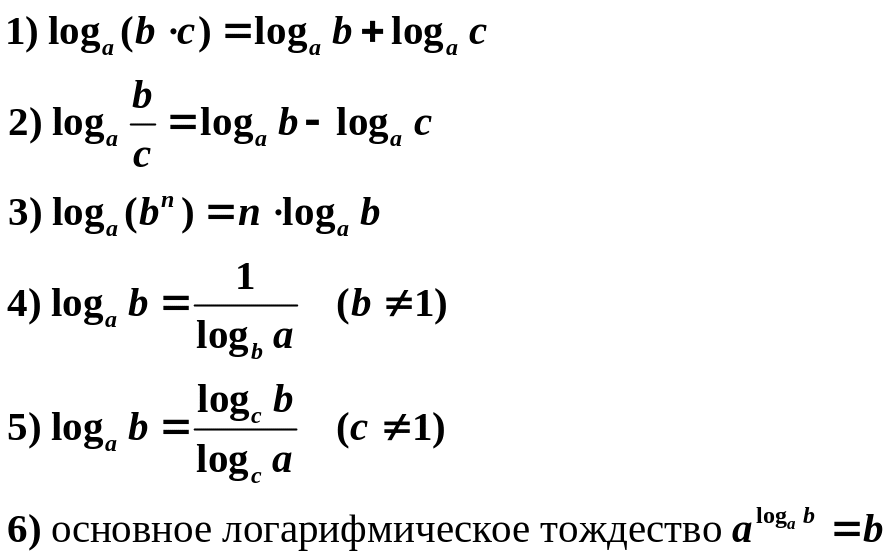
где

4. Тригонометрические формулы

5. Таблица производных

6. Правила дифференцирования

1) 2)

3) 4)

5) 6)

7. Таблица дифференциалов

45